Two billiard balls are rolling on a flat table. One has the velocity components vx=1ms−1,vy=√3ms−1 and the other has components v'x=2ms−1 and v'y=2ms−1. If both the balls start moving from the same point, what is the angle between their paths ?
To find the angle between the paths of the two billiard balls, we can follow these steps:
Step 1: Write the velocity vectors
The velocity components of the first billiard ball are given as:
- vx=1ms−1
- vy=√3ms−1
Thus, the velocity vector v1 can be written as:
v1=1^i+√3^j
The velocity components of the second billiard ball are:
- v′x=2ms−1
- v′y=2ms−1
Thus, the velocity vector v2 can be written as:
v2=2^i+2^j
Step 2: Calculate the dot product of the vectors
The dot product v1⋅v2 is calculated as follows:
v1⋅v2=(1)(2)+(√3)(2)=2+2√3
Step 3: Calculate the magnitudes of the vectors
The magnitude of v1 is:
|v1|=√(1)2+(√3)2=√1+3=√4=2
The magnitude of v2 is:
|v2|=√(2)2+(2)2=√4+4=√8=2√2
Step 4: Use the dot product to find the cosine of the angle
Using the formula for the dot product:
v1⋅v2=|v1||v2|cosθ
We can substitute the values we found:
2+2√3=(2)(2√2)cosθ
This simplifies to:
2+2√3=4√2cosθ
Step 5: Solve for cosθ
Rearranging gives:
cosθ=2+2√34√2=1+√32√2
Step 6: Calculate the angle θ
To find θ, we take the inverse cosine:
θ=cos−1(1+√32√2)
Step 7: Determine the angle in degrees
Using known values, we can find that:
θ≈15∘
Thus, the angle between the paths of the two billiard balls is 15∘.
---
The velocity components of the first billiard ball are given as:
- vx=1ms−1
- vy=√3ms−1
v1=1^i+√3^j
- v′x=2ms−1
- v′y=2ms−1
v2=2^i+2^j
The dot product v1⋅v2 is calculated as follows:
v1⋅v2=(1)(2)+(√3)(2)=2+2√3
The magnitude of v1 is:
|v1|=√(1)2+(√3)2=√1+3=√4=2
|v2|=√(2)2+(2)2=√4+4=√8=2√2
Using the formula for the dot product:
v1⋅v2=|v1||v2|cosθ
We can substitute the values we found:
2+2√3=(2)(2√2)cosθ
This simplifies to:
2+2√3=4√2cosθ
Rearranging gives:
cosθ=2+2√34√2=1+√32√2
To find θ, we take the inverse cosine:
θ=cos−1(1+√32√2)
Using known values, we can find that:
θ≈15∘
Topper's Solved these Questions
- VECTORSBOOK - SL ARORACHAPTER - VECTORSEXERCISE - TYPE B
2 Videos
- VECTORSBOOK - SL ARORACHAPTER - VECTORSEXERCISE - TYPE C
2 Videos
- VECTORSBOOK - SL ARORACHAPTER - VECTORSEXERCISE - Problems For Self Practice
56 Videos
- Units and MeasurementsBOOK - SL ARORACHAPTER - Units and MeasurementsEXERCISE - Exercise
499 Videos
- WAVE MOTIONBOOK - SL ARORACHAPTER - WAVE MOTIONEXERCISE - All Questions
271 Videos
Similar Questions
Two particles A and B are moving in the x−y plane such that their velocity components are vx=1m/s,vy=1√3m/s (for A) and vx=2m/s,vy=2m/s (for B). If both the particles start moving from the same point, what is the angle between their paths ?
View SolutionA velocity of 10ms−1 has its Y-component 5√2ms−1. Calculate its X-component.
View Solution
Knowledge Check
Two balls are rolling on a flat surface. One has velocity components m/s and √3m/s along the rectangular axes x and y, respectively and the other has component 2m/s and 2m/s, respectively. If both the balls start moving from the same point, the angle between their directions of motion is
A15∘B30∘C45∘D60∘Two balls are rolling on a flat smooth table. One ball has velocity components √3ˆj and ˆi while the other has components 2ˆi and 2ˆj. If both start moving simultaneously from the same point, the angle between their paths is-
A15∘B30∘C45∘D60∘Two billiard balls are moving on a table and the component velocities along the length and breadth are 5,5 ms−1 for one ball 2√32ms−1 for the other ball the angle between the motion of balls is
A30∘B60∘C40∘D15∘
Two billiard ball, rolling a flat table, have started moving from the same point. If their x components of velocities are √3m/s and 2m/s and y components of velocities are 1m/s and 2m/s , respectively, calculate the angle between their paths .
View SolutionFind the equation of trajectory of a particle whose velocity components are
vx=2x+1,vy=2y+3
Given that particle starts from rest from origin.
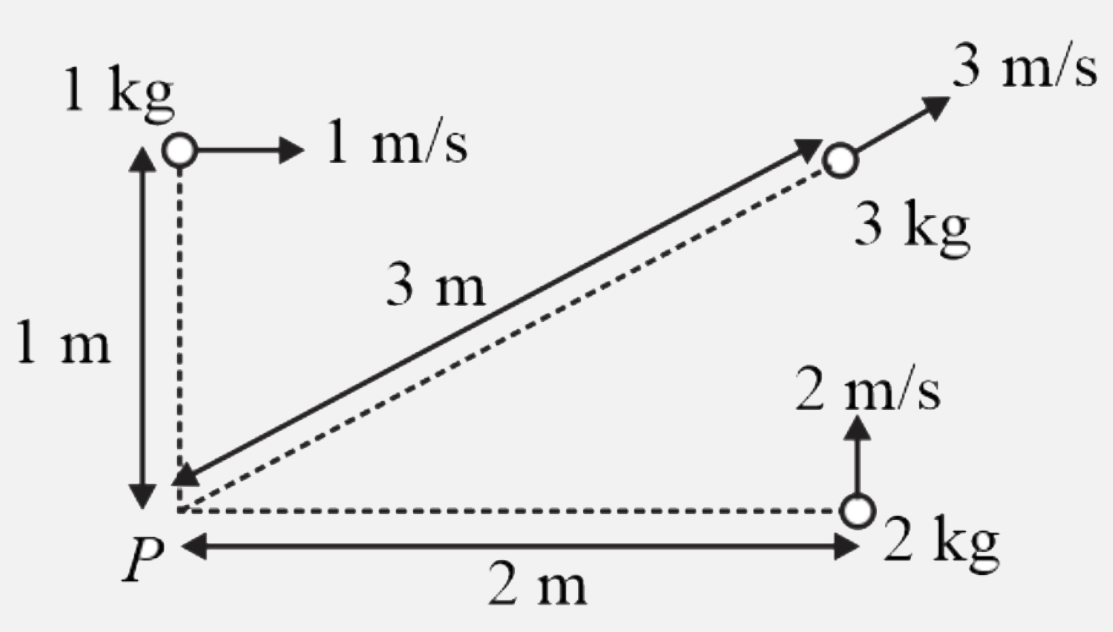
View SolutionThree small balls of masses 1kg, 2kg and 3kg are moving in a plane and their velocities are 1ms−1,2ms−2and3ms−1 respectively as shown . The total angular momentum of the system of three balls about point P at the given instant of time is
View SolutionA particle is moving in the x-y plane. At certain instant of time, the components of its velocity and acceleration are as follows: vx=3ms−1,vy=4ms−1,ax=2ms−2anday=1ms−2. The rate of change of speed at this moment is
View SolutionThe collision of two balls of equal mass takes place at the origin of coordinates. Before collision, the components of velocities are (vx=50cm−1 , vy=0) and (vx=−40cm−1 and vy=30cms−1. The first ball comes to rest after collision. The velocity (components vx and vy respectively) of the second ball are
View Solution
