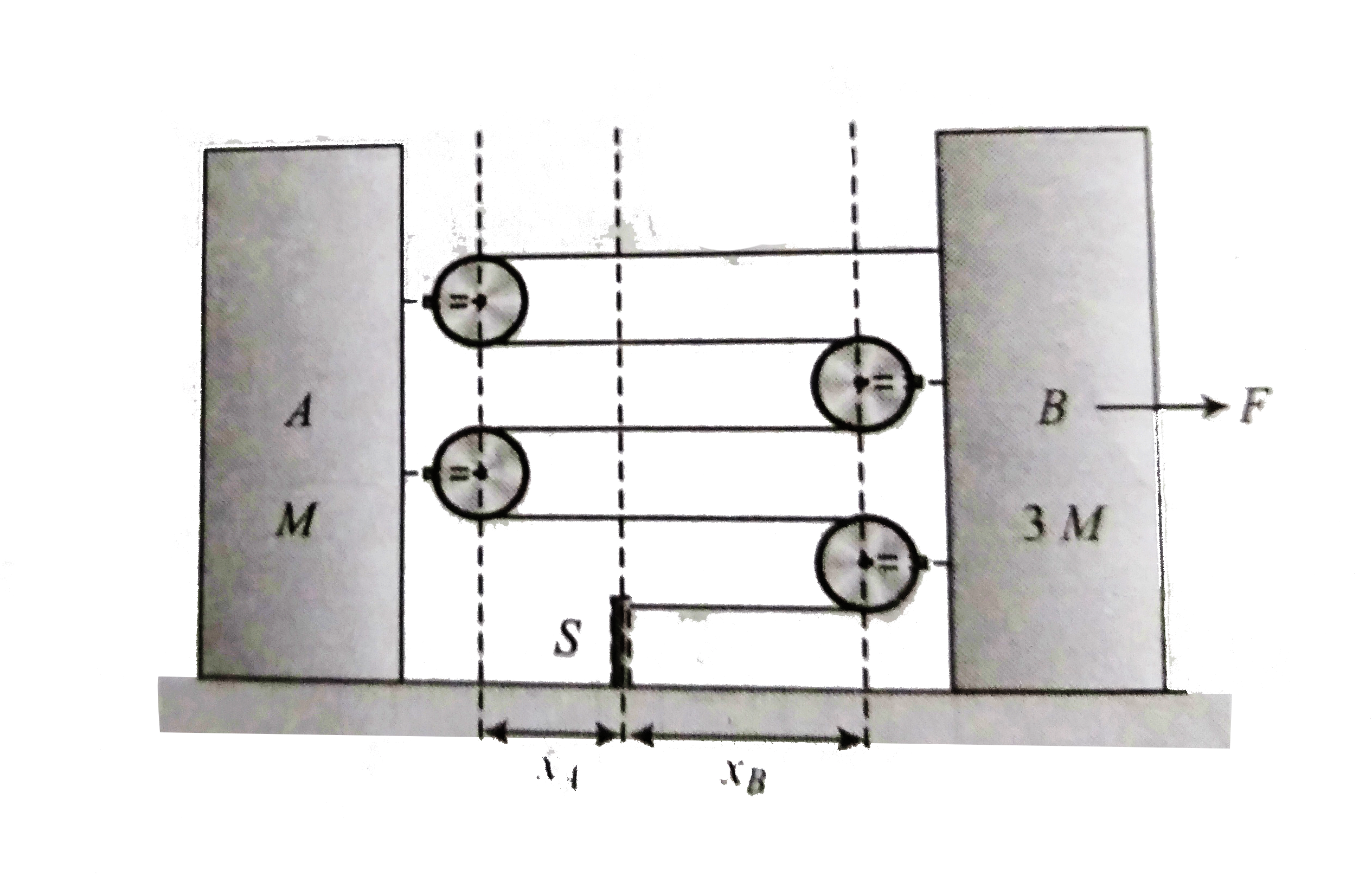
Two block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

Taking reference line through support S let xA and xB are the distances of blocks A and B, respectively, from S. The total length of the string, l=4xA+5xB+l0. Where l0 is some part of string which is over pulley and somewhere else which remains constant.
Differentiating l w.r.t time, we get
dldt=ddt(4xA5xB+l0)
or 0=4dxadt+5dxBdt=dxAdt=54dxBdt
dxAdt=−vA (-because xA is decreasing with time)
dxBdt=−vB (+because xB is decreasing with time)
or vA=54vB,alsoaA=54aB
Method 2: charge in the length of segment I, Δl1,2=0+(xB)

Segment II
Δl3.4=(−xA)+(xB)
Segment III
Δl5,6=(−xA)+(xB)
Segment IV
Δl7,8=(−xA)+(xB)
Segment V
Δl9,10=(−xA)+(xB)
Total charge in segment lengths should be zero. Therefore,
Δl=Δl1,2+Δl3,4+Δl5,6+Δl7,8+Δl9,10=0
=xB+[−xA+xB]+[−xA+xB]
+[−xA+xB]+[−xA+xB]=0
=−4xA+5xB=0
or xA=54xB⇒vA=54vB⇒aA=54aB
Equation of motion

For A:
4T=mAaA=MaA...(i)
For B:
F−5T=mBaB=3MaB ..(ii)
aB=16F73
and aA=54×(16F73)=20F73.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A block B is m kept on an inclined plane. Anotherblock A is inserted in a slot in the block B though a light string. One end of the string is fixed to a support and other end of the string is attached to A. All the surfaces are smooth. Masses of A and B are same. The acceleration of block B is found to be 4/n.Find value of n.
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
View Solution
Knowledge Check
A block A of mass m is attached at one end of a light spring and the other end of the spring is connected to another block B of mass 2m through a light string as shown in the figure. A is held and B is in static equilibrium. Now A is released. The acceleration of A just after that instant is a . In the next case, B is held and A is in static equilibrium. Now when B is released, its acceleration immediately after the release is b . The value of a/b is (pulley, string and the spring are massless).
 A0BundefinedC2D12
A0BundefinedC2D12Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the planeTwo Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
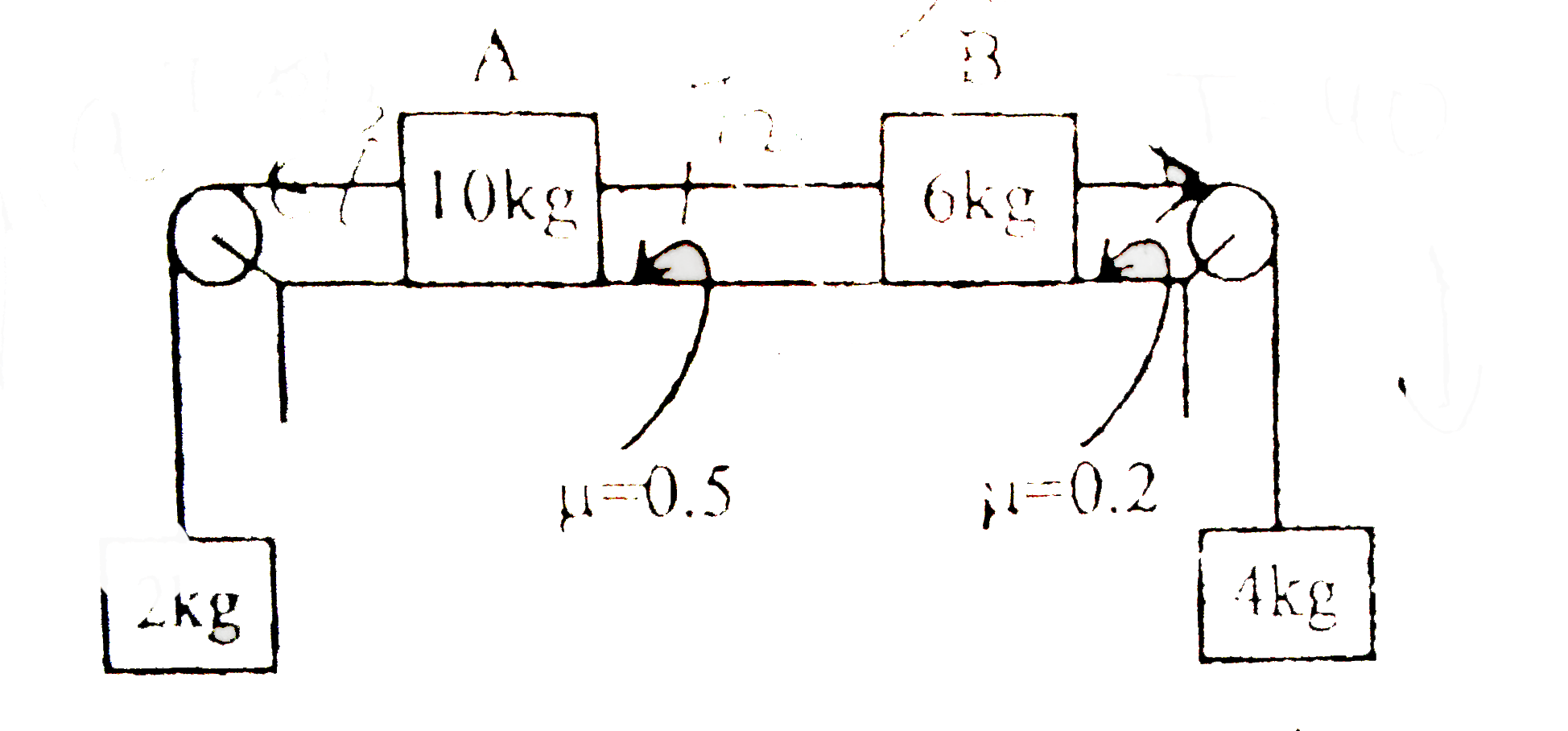 A0B76C1011D3011
A0B76C1011D3011
Two block of masses m=5kgandM=10kg are connected by a string passing over a pulley B as shown. Another string connect the center of pulley B to the floor and passes over another pulley A as shown. An upwards force F is applied at the center of pulley A. Both the pulleys are massless.
Find the acceleration of block m and M, if F is
(a) 100N
300N
500N(Takeg=10m/s2)

View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
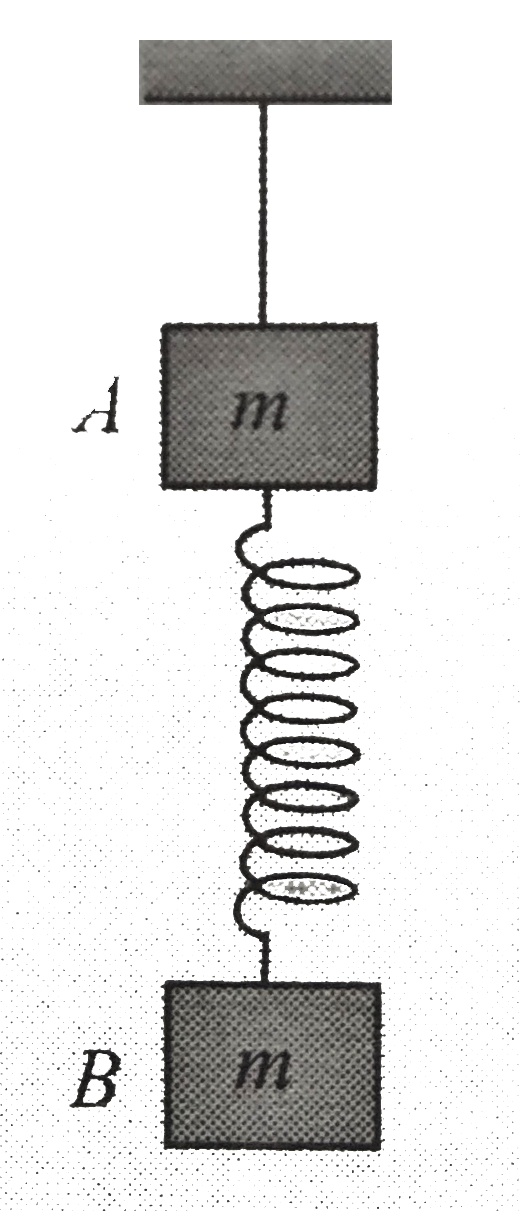
View SolutionTwo blocks A and B of same mass m attached with a light string are suspended by a spring as shown in fig. Find the acceleration of block A and B just after the string is cut.

View SolutionTwo blocks o equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constnt force F. Find the tension in the string joining the blocks.
View SolutionThe figure shown blocks A and B are mass 2 kg and 8 kg and they are connected through strings to a spring connected to ground. The blocks are in equilbrium. (g=10m/s2)

Now the force on A is suddenly removed. The acceleration of block B becomes :-
View Solution
