Two block A and B of masses 6kg and 3kg rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is 0.4 the maximum horizontal force which can make them move without separation is

72N
40N
36N
20N
The correct Answer is:C
Maximum friction force on block B is
μmBg=0.4×3×10=12N
Hence, maximum acceleration =123=4ms−1
Hence , maximum force
F=(mA+mB)a=(6+3)×4=36N
Afiber We can also apply the formula discussed in pervious problem by putting μ2=0andμ1=0.4
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two blocks of masses 4kg and 6kg are kept on a rough horizontal surface as shown. If the acceleration of 6kg block is 5n, then n is :

View SolutionTwo blocks of mass 2kg and 1kg are at rest on a smooth surface as shown. There is friction between 2kg and 1kg block with μ=0.5. Find maximum force to be applied on 1 kg for the two blocks to move together.
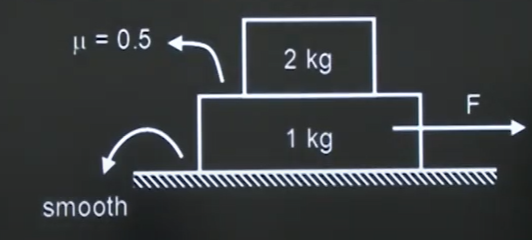
View Solution
Knowledge Check
Two block A and B of masses 5 kg. and 3 kg. respectively rest on smooth horizontal surface with B over A. The coefficient of friction between A and B. 0.5 the maximum horizontal force that can be applied to A so that there will be motion of A and B without separation is :-
A15B25C40D50Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
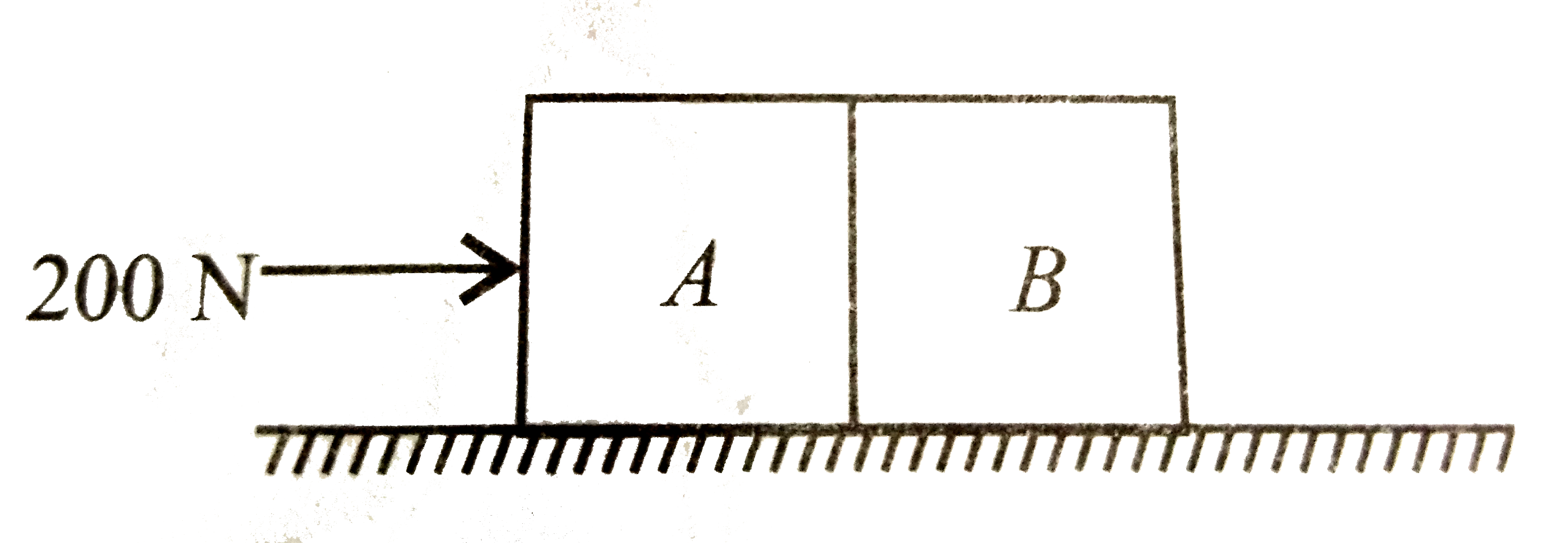 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
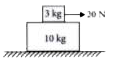
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
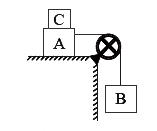
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionTwo block (A) 2kg and (B) 5kg rest one over the other on a smooth horizontal plane. The cofficient of static and dynamic friction between (A) and (B) is the sae and equal to 0.60. The maximum horizontal force that can be applied to (B) in order that both (A) and (B) do not have any relative motion:
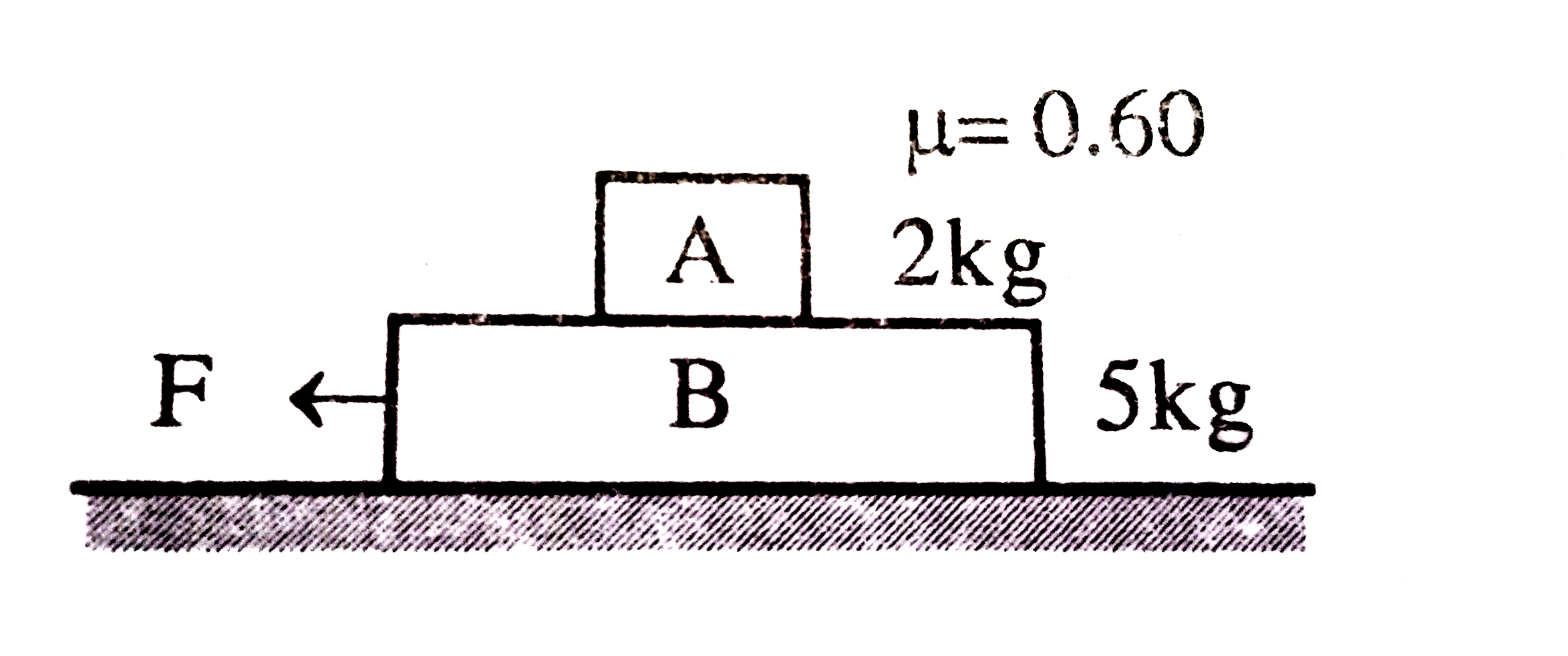
View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is μ=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

View Solution
