Two block of masses M1andM2 are connected with a string passing over a pulley as shown in figure The block M1 lies on a horizontal surface friction between the block M1 and the horizontal surface is μ The system accelerates. What additional mass m should be plased on the block M1 so that the system does not accelerate ?
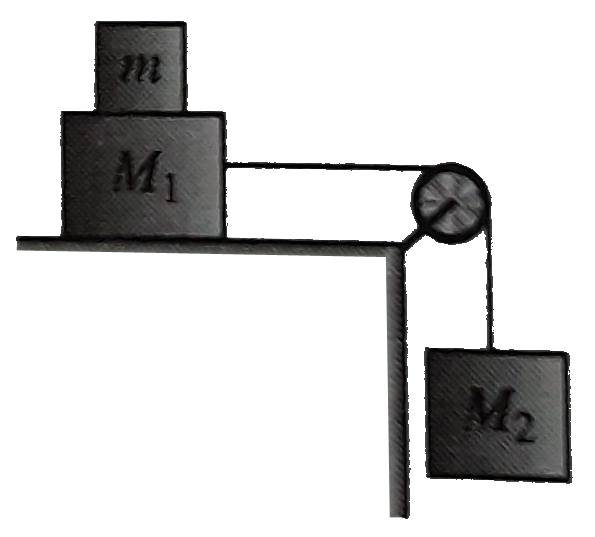
M2−M1μ
M2μ−M1
M2−M1μ
(M2−M1)μ
The correct Answer is:b
For the equilibrium of block of mass M1:
friction force f= tension in the string T
whereT=f=μ(m+M1)g
For the equilkibrium of block of mass M2
T=M2g
From Eqs (i) and (ii)we getμ(m+M1)g=M2g
m=M2μ−M1
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View Solution
Knowledge Check
Two blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
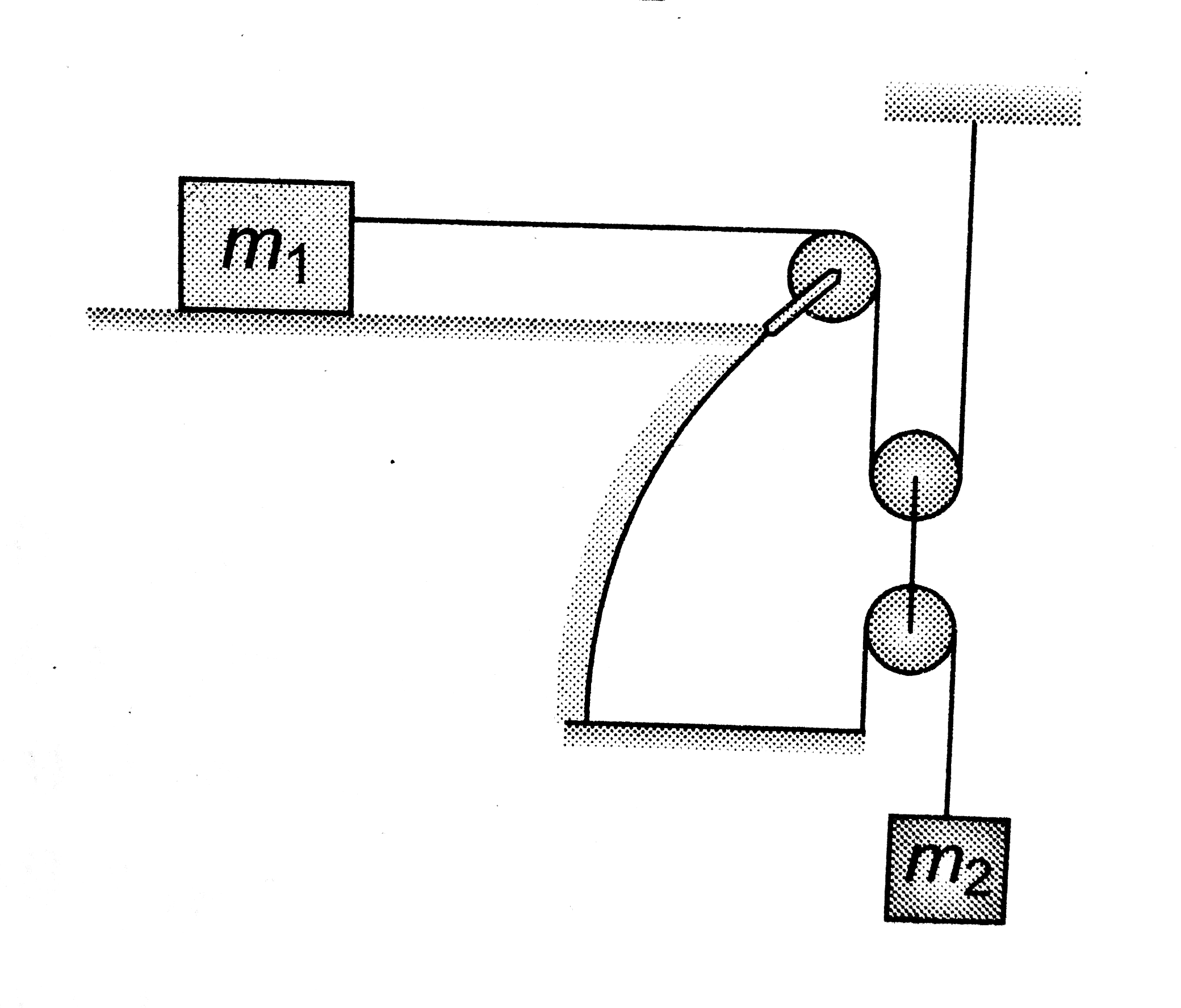 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
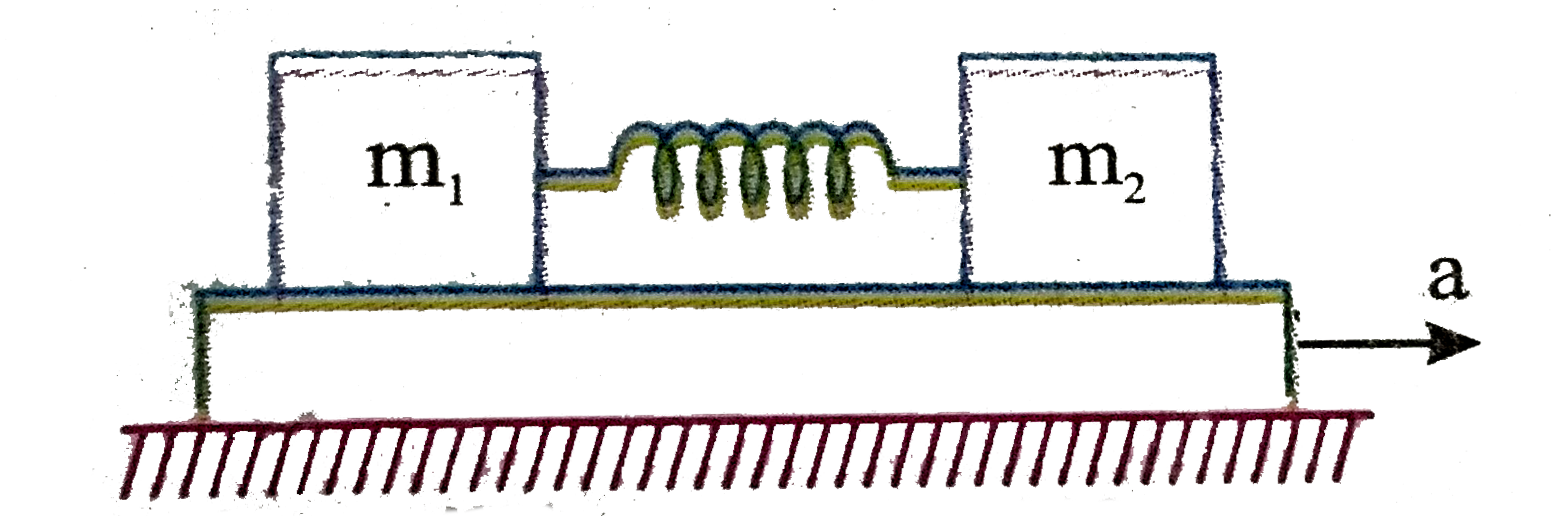 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Blocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
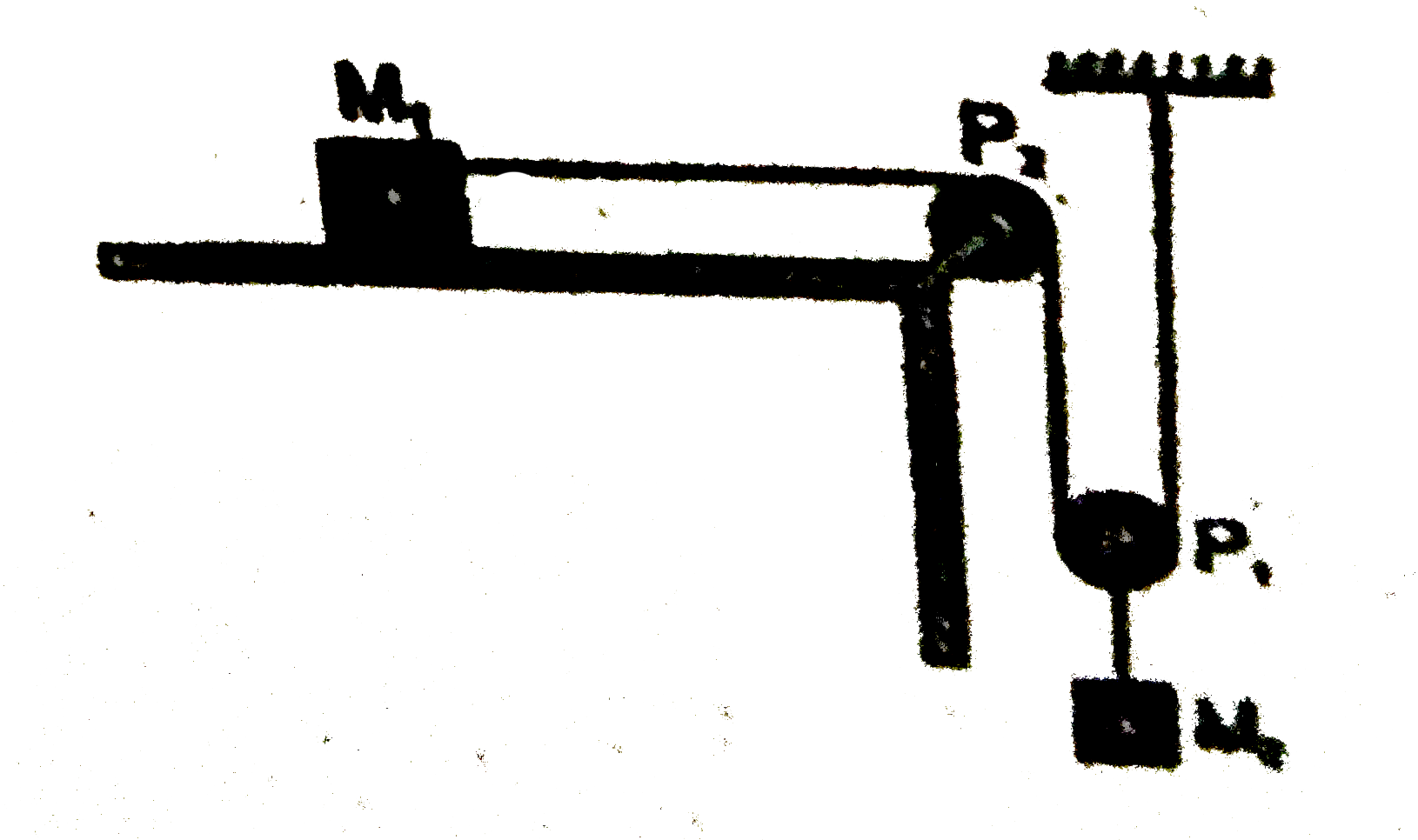
View SolutionTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?

View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
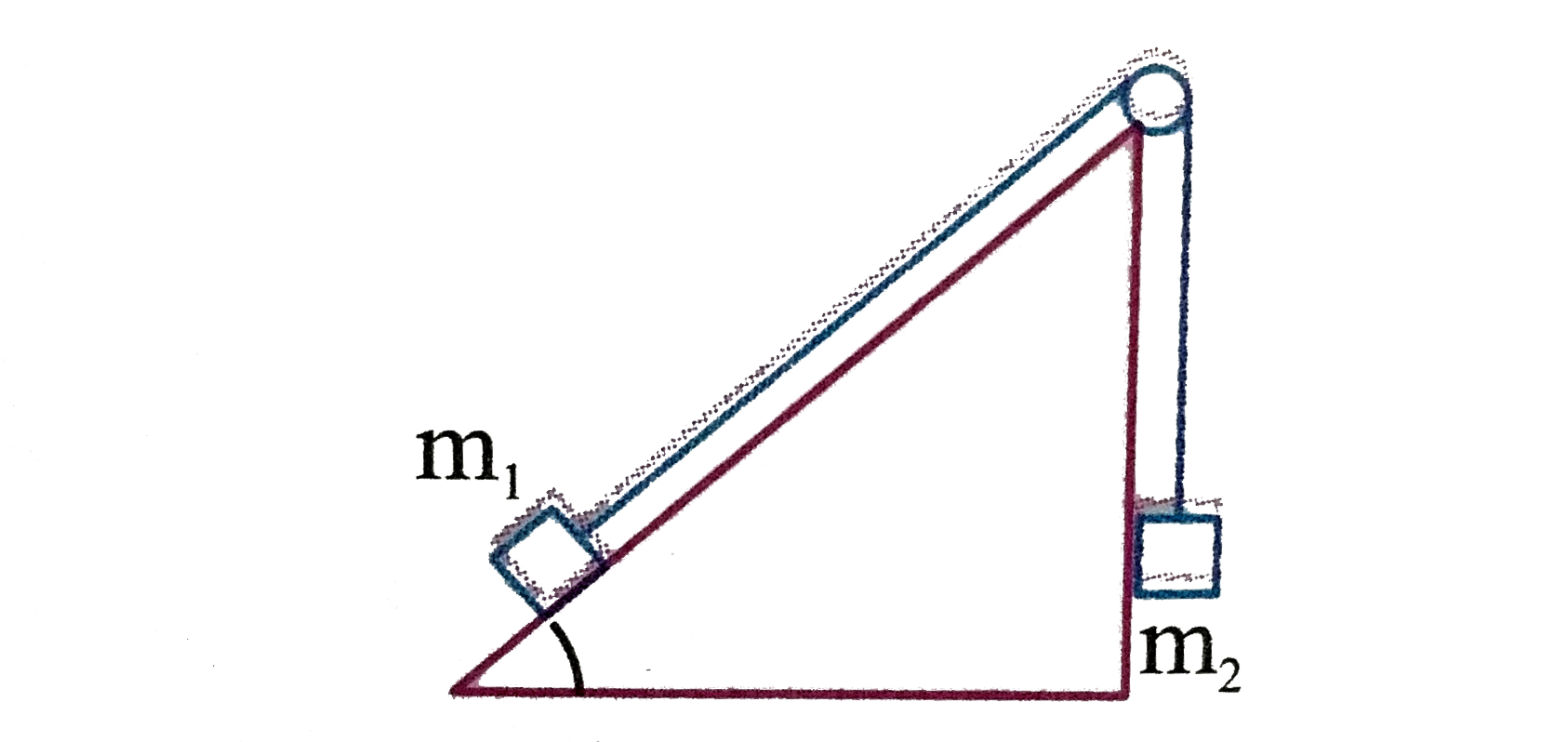
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View Solution
