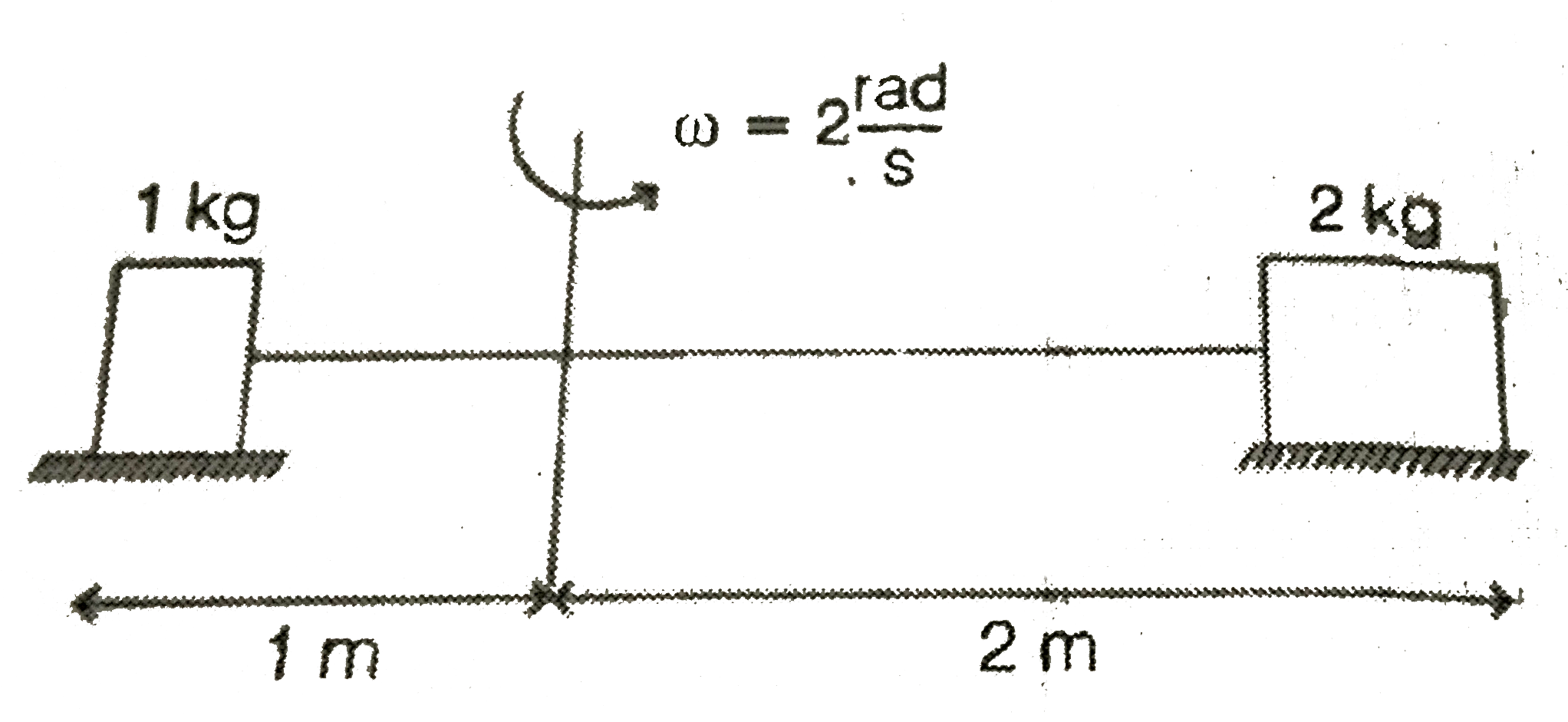
Two block tied with a massless string of length 3m are placed on a rotating table as shown. The axis of rotation is 1m from 1kg mass and 2m from 2kg mass. The angular speed ω=4rad/s . Ground below 2kg block is smooth and below 1kg block is rough. (g=10m/s2)
(a) Find tension in the string, force of friction on 1kg block and its direction.
(b) If coefficient of friction between 1kg block and groung is μ=0.8. Find maximum angular speed so that neither of the blocksd slips.
(c) If maximum tension in the string can be 100N , then maximum angular speed so that neither of the blocks slips. 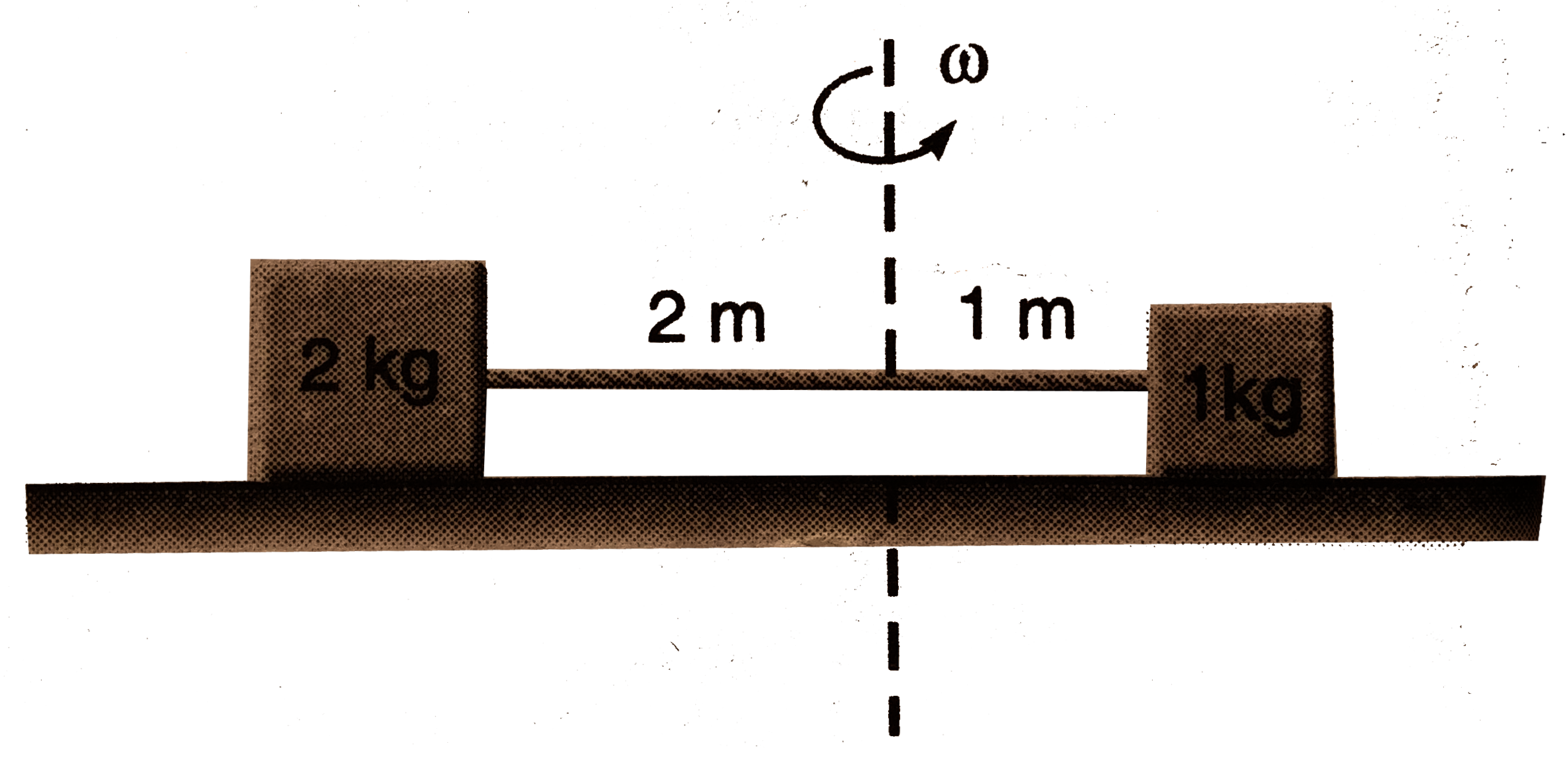
The correct Answer is:A, B, C, D
2Kg→T
T=m2r2ω2=(2)(2)(4)2=64N
Centripetal force required to 1Kg block is

Fc=m1r1ω2=(1)(1)(4)2=16N
But available tensions is 64N . So, the extra force of 48N is balance by friction acting radially outward from the centre.
(b) fmax=μ1g=0.8×1×10=8N

T=m2r2ω2=(2)(2)ω2=4ω4
T−8=m1r1ω2=(1)(1)(ω2)=ω2
Solving Eqs. (i) and (ii) we get,
ω=1.63rad/s
(c) T=m2r2ω2
2Kg→T
→m2r2ω2
:. 100=(2)(2)ω2
or ω=5rad/s
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective
14 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
In the figure shown, block of mass 2 kg is very long. Force of friction on 1 kg block is
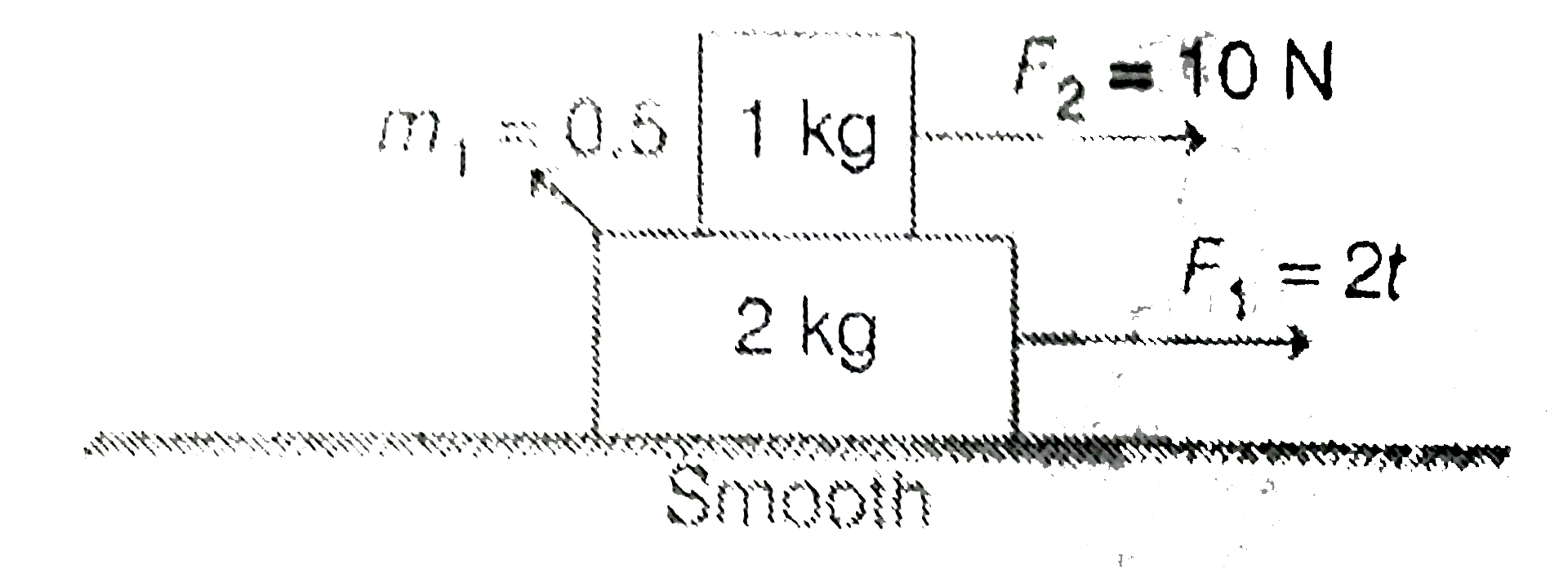
View SolutionIn the diagram shown coefficient of friction between 2 kg block and 4 kg block is μ=0.1 and between 4 kg and ground is μ=0.2 then answer the following quwstions .(tis time)
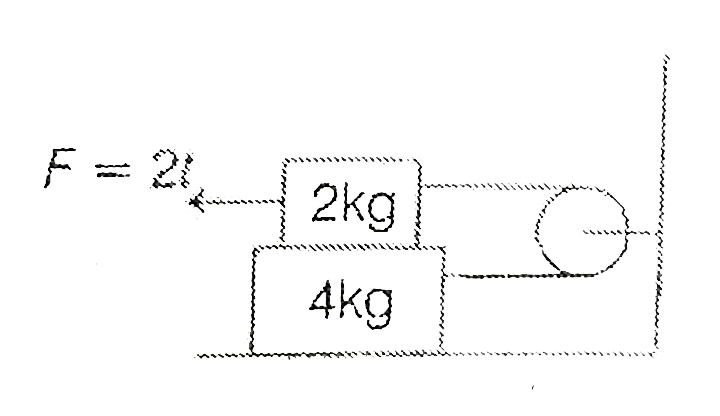
Force of friction on 2 kg block at t=12 s will be
View SolutionTwo blocks of mass 4kg and 2kg are connected by a heavy string and placed on rough horizontal plane. The 2 kg block is pulled with a constant force F. the coefficent of friction between the blocks and the ground is 0.5. what is the value of F so that tension in the string is constant throughout the length? (g=10m/s2)
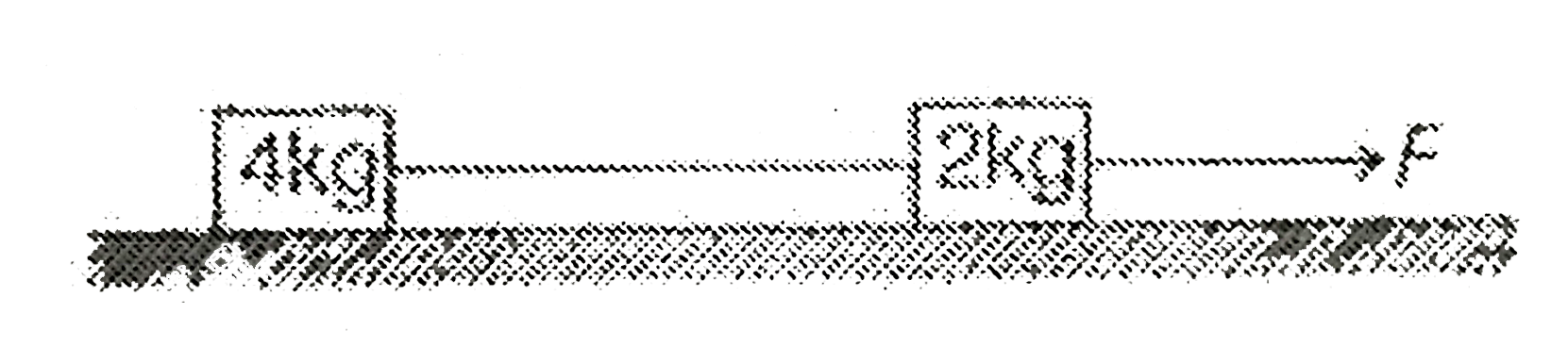
View SolutionThe tension in the string connected between blocks is

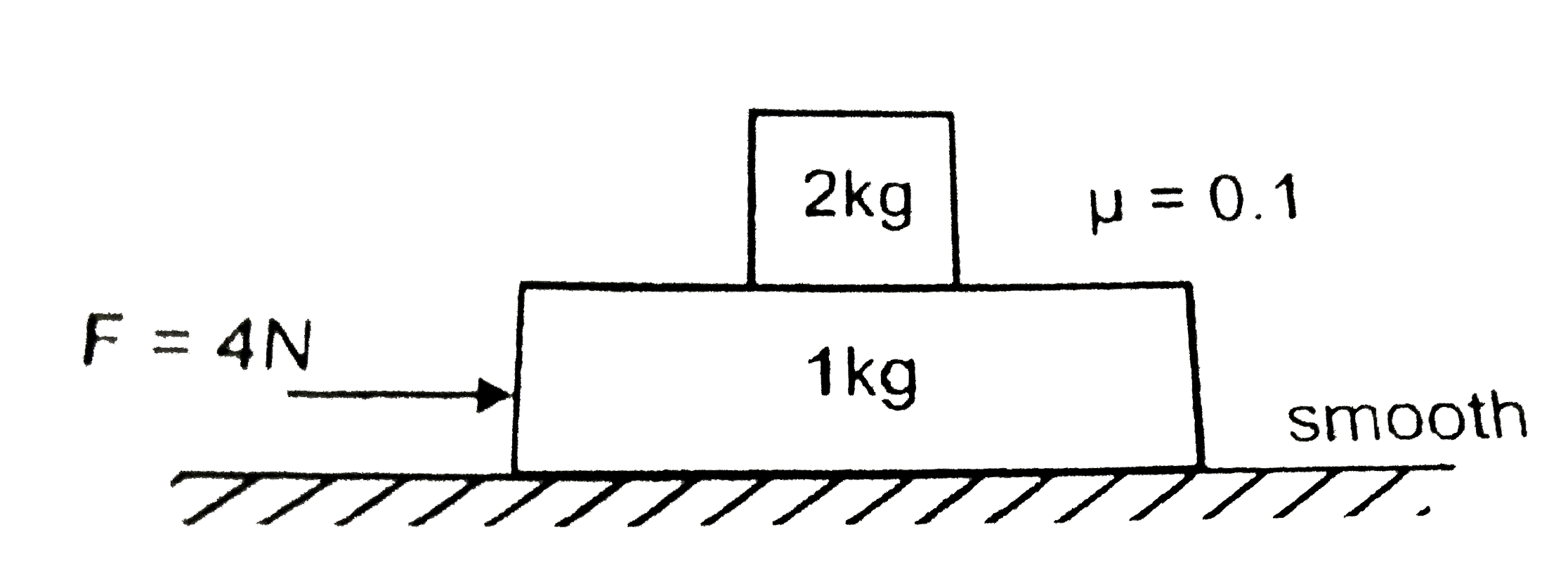
View Solution2gk block is kept on 1kg block as shown . The friction between 1kg block and fixed surface is absent and the coefficient of friction between 2kg block is μ=0.1. A constant horizontal force F=4N is applied on 1kg block. If the work done by the friction on 1kg block in 2s is −XJ, then find X. Take g=10m/s2.
View SolutionIn figure shown if 2 kg block is moving at an acceleration 2m/s2, find the elongationin spring and acceleration of 4 kg block at this instant. Take g= 10m/s2.
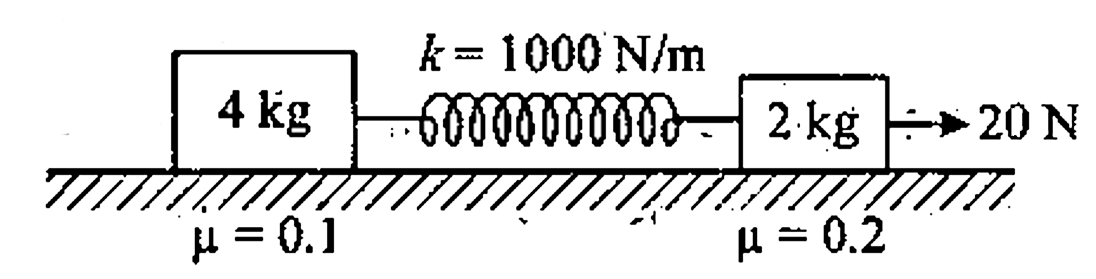
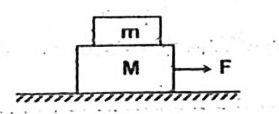
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
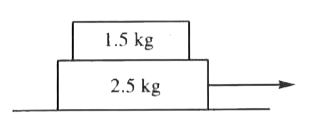
View SolutionOn a smooth table two blocks of masses 2.5kg and 1.5kg are placed one over the other as shown in figure. If the coefficient of static friction between two blocks is 0.2, the maximum horizontal force to be applied on the lower block so that the two blocks move together is (g = ms−2)
View SolutionTwo blocks of masses 1 kg and 2 kg are joined by a massless inextensible string of length 3m. Both blocks are kept on a horizontal table as shown. Friction coefficient between 2 kg block and table is zero. They are rotated about a vertical axis passing at a distance of 1m from 1 kg. Force of friction on 1kg block is (assume that there is enough friction between 1 kg block ground)
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View Solution
