Two blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
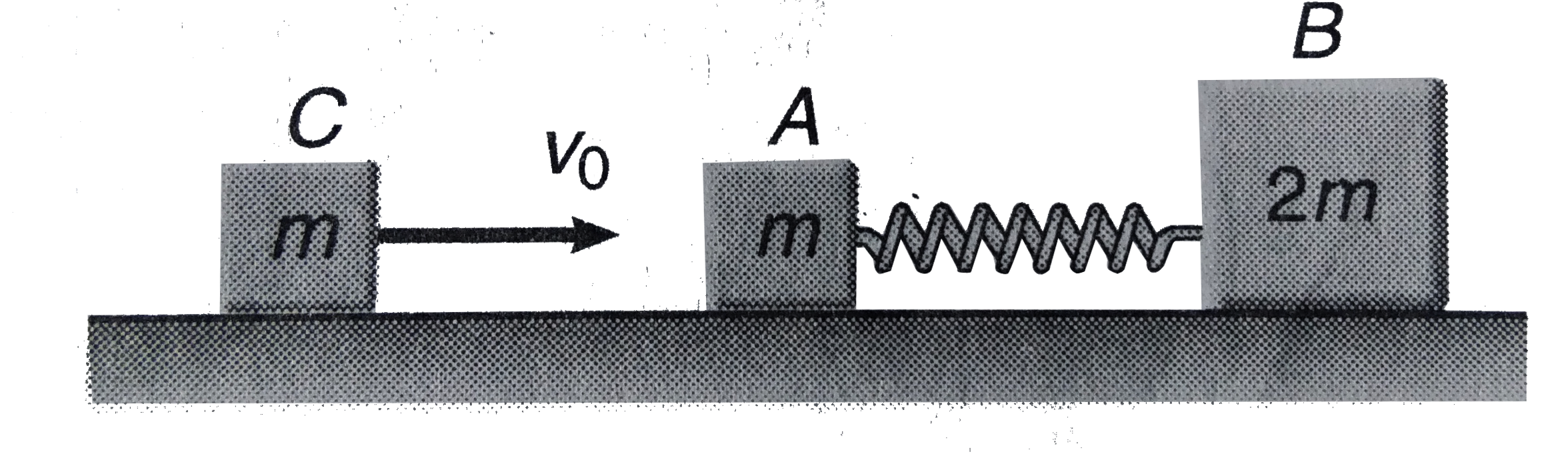
The correct Answer is:B, C
Initially, the blocks A and B are at rest and C is moving with velocity v0 to the right. As masses of C and A are same and the collision is elastic the body C treansfers its whole momentum mv0 to body A and as a result the body C stops and A starts moving with velocity v0 to the right. As this instant the spring is uncompressed and the body B is still at rest.
The momentum of the system at this instant =mv0
Now, the spring is compressed and the body B comes in motion. After time t0, the compression of the spring is x0 and common velocity of A and B is v(say).
As external force on the system is zero, the law of conservation of linear momentum gives
mv0=mv+(2m)v or v=v03
The law of conservation of energy gives
12mv20=12mv2+12(2m)v2+12kx20
or 12mv20=32mv2+12kx20
12mv20=32m(v03)2+12kx20
∴12kx20=12mv20−16mv20
or 12kx20=13mv20
k=23mv20x20
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two bodies A and B of masses m and 2 m respectively are placed on a smooth floor. They are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A as shown in Fig.

At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

View Solution
Knowledge Check
Two blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:
 Athe common velocity of A and B at time t0 is v/3Bthe spring constant is k=mv202x20Cthe spring constant is k=2mv203x20Dnone of these
Athe common velocity of A and B at time t0 is v/3Bthe spring constant is k=mv202x20Cthe spring constant is k=2mv203x20Dnone of theseA ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatjA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?
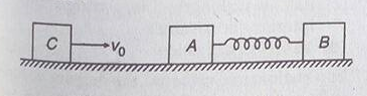 Amv20x20Bmv202x20C32mv20x20D23mv20x20
Amv20x20Bmv202x20C32mv20x20D23mv20x20
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View Solution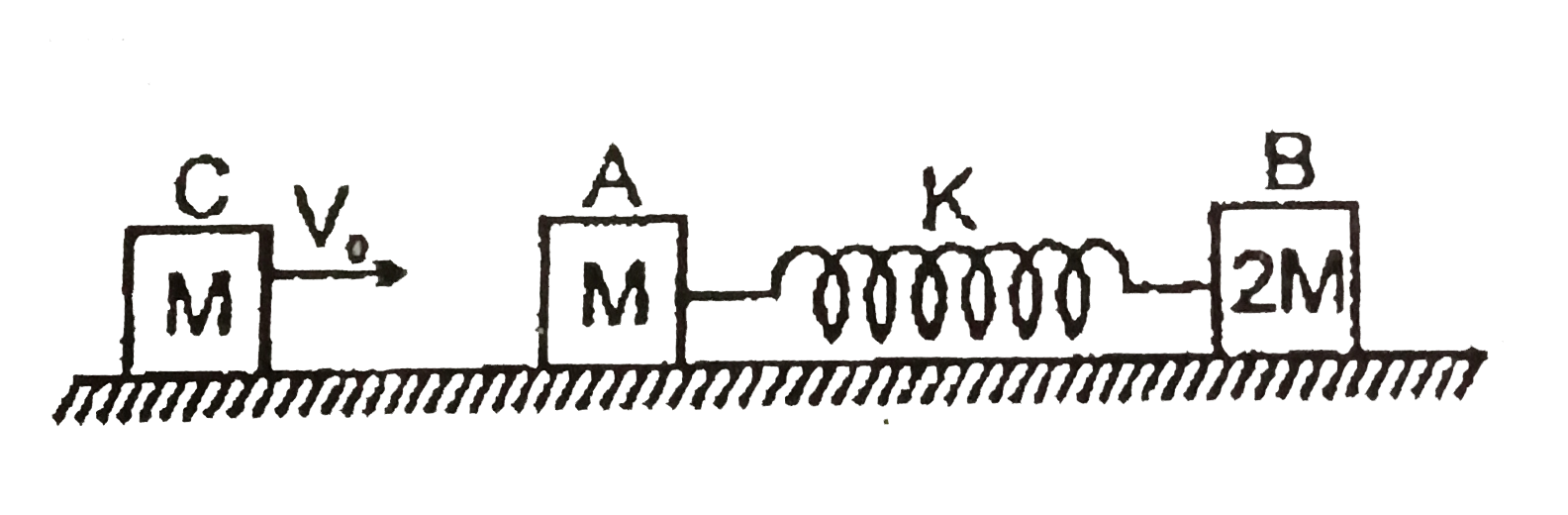 Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring

View SolutionA block C of mass m is moving with velocity v0 and collides elastically with block A of mass m and connect to another block B of mass 2m through spring constant k. What is k if x0 is compression of spring when velocity of A and B is same ?

View Solution
