Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
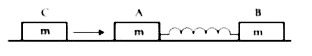
√mvK
v√m2K
√mv2K
√m2K
Step by step video & image solution for Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

View Solution
Knowledge Check
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2kTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
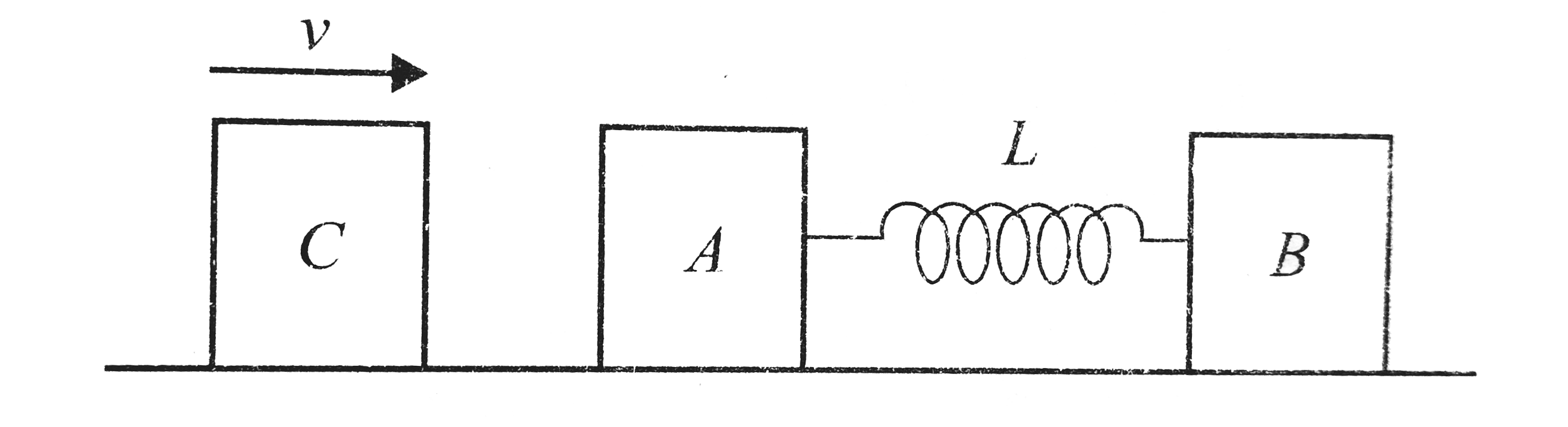
Av√m2kBv√v2kC√mvkDmv2kTwo blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
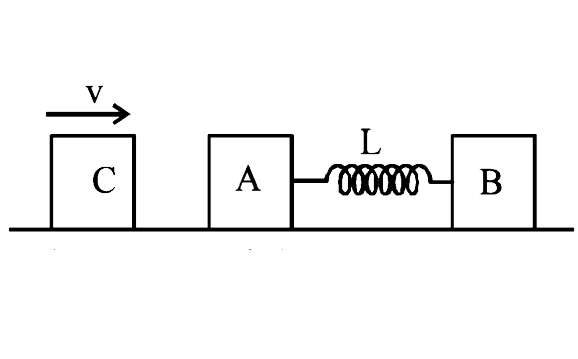
Two blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -

View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
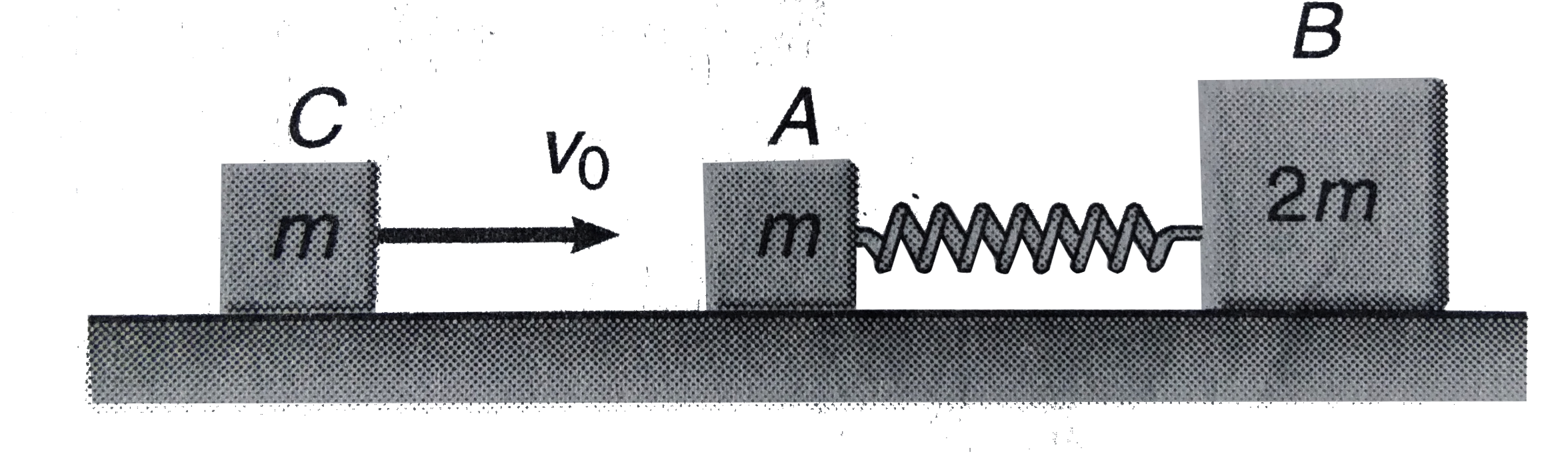
View SolutionTwo blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
View SolutionTwo blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:

View Solution
