Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
30m/s
20m/s
10m/s
5m/s
The correct Answer is:C
To solve the problem, we need to find the velocity of the center of mass of the system consisting of two blocks with masses 10 kg and 4 kg after an impulse is applied to the heavier block. Here’s a step-by-step solution:
Step 1: Identify the masses and initial conditions
- Let m1=10kg (mass of the heavier block)
- Let m2=4kg (mass of the lighter block)
- The initial velocity of the heavier block v1=14m/s (after the impulse)
- The initial velocity of the lighter block v2=0m/s (it is at rest)
Step 2: Use the formula for the velocity of the center of mass
The velocity of the center of mass Vcm of a system of particles is given by the formula:
Vcm=m1v1+m2v2m1+m2
Step 3: Substitute the known values into the formula
Substituting the values we have:
Vcm=(10kg⋅14m/s)+(4kg⋅0m/s)10kg+4kg
Step 4: Calculate the numerator and denominator
Calculating the numerator:
10⋅14+4⋅0=140+0=140
Calculating the denominator:
10+4=14
Step 5: Calculate the velocity of the center of mass
Now, substituting back into the equation:
Vcm=14014=10m/s
Final Answer
The velocity of the center of mass is 10m/s.
---
- Let m1=10kg (mass of the heavier block)
- Let m2=4kg (mass of the lighter block)
- The initial velocity of the heavier block v1=14m/s (after the impulse)
- The initial velocity of the lighter block v2=0m/s (it is at rest)
The velocity of the center of mass Vcm of a system of particles is given by the formula:
Vcm=m1v1+m2v2m1+m2
Substituting the values we have:
Vcm=(10kg⋅14m/s)+(4kg⋅0m/s)10kg+4kg
Calculating the numerator:
10⋅14+4⋅0=140+0=140
Calculating the denominator:
10+4=14
Now, substituting back into the equation:
Vcm=14014=10m/s
The velocity of the center of mass is 10m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - MCQ_TYPE4videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - AR_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2 - Question 2 - Select One
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View SolutionTwo blocks of masses 5kg and 2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
View SolutionTwo blocks of masses 5kgand2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are respectively :
View SolutionFigure shows two blocks of masses 5kg and 2kg placed on a frictionless surface and connected with a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. Deduce (a) velocity gained by the centre of mass and (b) the separate velocities of the two blocks in the centre of mass coordinates just after the kick.
 View Solution
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
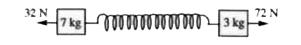 View Solution
View Solution

