Two blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
4m/s
5m/s
2m/s
3m/s
To find the velocity of the center of mass of the system consisting of two blocks connected by a spring, we can follow these steps:
Step 1: Identify the masses and initial conditions.
Let:
- Mass of the first block (m1) = 5 kg
- Mass of the second block (m2) = 2 kg
- Initial velocity of the first block (v1) = 7 m/s (given)
- Initial velocity of the second block (v2) = 0 m/s (since it is at rest)
Step 2: Use the formula for the velocity of the center of mass (V_cm).
The formula for the velocity of the center of mass (V_cm) for a system of particles is given by:
Vcm=m1v1+m2v2m1+m2
Step 3: Substitute the known values into the formula.
Substituting the known values into the formula:
Vcm=(5kg×7m/s)+(2kg×0m/s)5kg+2kg
Step 4: Calculate the numerator and denominator.
Calculating the numerator:
5kg×7m/s=35kg m/s
2kg×0m/s=0kg m/s
So, the total momentum (numerator) is:
35kg m/s+0kg m/s=35kg m/s
Calculating the denominator:
5kg+2kg=7kg
Step 5: Calculate the velocity of the center of mass.
Now substituting back into the formula:
Vcm=35kg m/s7kg=5m/s
Final Answer:
The velocity of the center of mass is 5 m/s.
---
Let:
- Mass of the first block (m1) = 5 kg
- Mass of the second block (m2) = 2 kg
- Initial velocity of the first block (v1) = 7 m/s (given)
- Initial velocity of the second block (v2) = 0 m/s (since it is at rest)
The formula for the velocity of the center of mass (V_cm) for a system of particles is given by:
Substituting the known values into the formula:
Calculating the numerator:
2kg×0m/s=0kg m/s
Now substituting back into the formula:
The velocity of the center of mass is 5 m/s.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)
60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
View SolutionTwo blocks of masses 5kgand2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are respectively :
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks of masses 5kg and 2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
View SolutionFigure shows two blocks of masses 5kg and 2kg placed on a frictionless surface and connected with a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. Deduce (a) velocity gained by the centre of mass and (b) the separate velocities of the two blocks in the centre of mass coordinates just after the kick.
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of oscillation is
View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
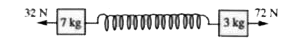
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View Solution
