Two' blocks of masses m, and m, are connected to the two ends of a string passing over a pulley as shown in figure. System hans vertically and blocks are held at rest. Assume that m1>m2. Find the speed attained by the blocks when m, descends through a height h. Moment of inertia of the pulley is I and its radius is r. There is enough friction between string and pulley so that there is no slipping between them.

⎷2(m1−m2)ghm1m2+Ir2
⎷2(m1+m2)ghm1m2+Ir2
⎷2m1m2mghm1+m2+Ir2
⎷(2m1−m2)mghm1+m2+Ir2
Since there is no slipping between string and the pulley hence there is no energy loss and total mechanical energy of the system remains conserved. Let v is the speed acquired by the blocks then angular speed of pulley must be v/r because there is no slipping between string and the pulley. For conservation of mechanical energy we can write the following:
Loss in gravitational potential energy of m1 = Gain in gravitational potential energy of m2+ Gain in K.E. of the blocks + gain K.E. of pulley.
⇒m1gh=m2gh+12(m1+m2)v2+12I(vr)2
⇒v=
⎷2(m1−m2)ghm1+m2+Ir2
Hence option (a) is correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Numerical Problems)
20 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Two blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.

View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solution
Knowledge Check
Two masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mgTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
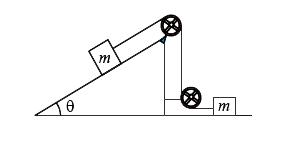
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionTwo blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
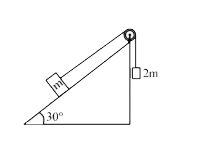
View Solution
