Two blocks of masses $m_{1}$ and $m_{2} (m_{1} > m_{2})$ in contact with each other on frictionless, horizontal surface. If a horizontal force F is given on $m_{1}$ set into motion with acceleration a, then reaction force on mass $m_{1}$ by $m_{2}$ isSolution in Tamil

Video Solution

Text Solution

Verified by Experts

Let us consider two blocks of masses $m_{1}$ and $m_{2} (m_{1} > m_{2})$ . Kept in contact with each other on a smooth horizontal frictional surface as shown in the figure

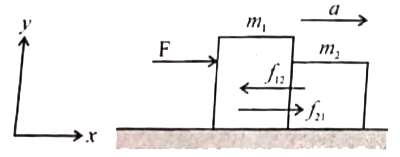
By the application of a horizontal force F both the blocks are set into motion with acceleration a simultaneously in the direction of the force F .
To find the acceleration $\to a$ Newton's second law has to be applied to the system mass $m = m_{1} + m_{2}$
If we select the motion of the two masses along the positive x direction $F ˆ j = m a ˆ i$
The acceleration of the system is given by
$∴, a = \frac{F}{m_{1} + m_{2}}$
The force exerted by teh block $m_{1}$ on $m_{2}$ due to its motion is called force of contact $(f_{n})$ According to Newton's third law the block $m_{2}$ will exert an equivalent opposite reaction
Figure shows the free body diagram of block $m_{1}$

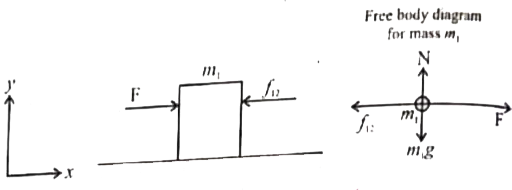
$F ˆ i - f_{12} ˆ i = m_{1} a ˆ i$
By comparing the components of the above equation we get
$F - f_{12} = m_{1} a$
$f_{12} = F - m_{1} a$
Substituting the value of acceleration from equation (1) in (2) we get
$f_{12} = f - m_{1} \frac{F}{m_{1} + m_{2}}$
$F_{12} = \frac{F m_{2}}{m_{1} + m_{2}}$
Equation (3) shows that the magnitude of contact force depends on mass $m_{2}$ which provides the reaction force . Note that this force is acting along the negative x direction $m_{1}$ is given by $f_{12} = - \frac{F m_{2}}{m_{1} + m_{2}}$
For $m_{2}$ there is only one force force acting on it the x direction and it is denoted by $f_{21}$ . this force is exerted by mass $m_{1}$ .the free body diagram for mass $m_{2}$ is shown in the figure .

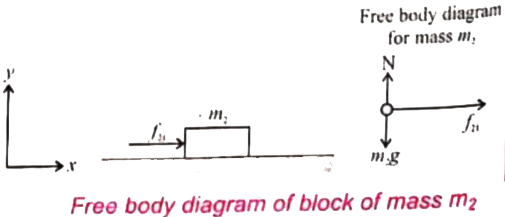
Applying Newton' second law for mass $m_{2}$
$f_{21} ˆ i = m_{2} ˆ i$
By comparing the components on both sides of the above equation
$f_{21} = m_{2} a$
Substituting for acceleration from equation
(1) in equation (4) we get
$f_{21} = \frac{F m_{2}}{m_{1} + m_{2}}$
In this case the magnitude of the contact force is $f_{21} = \frac{F m}{m_{1} + m_{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

PREMIERS PUBLISHERS-LAW OF MOTION -OTHER IMPORTANT QUESTIONS & ANSWERS (IV Long Answer Question )

Home
Ask Doubt
Profile