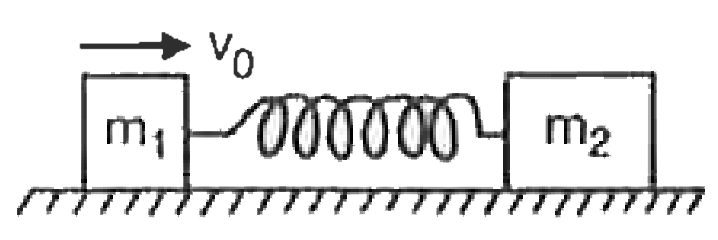
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
2 cm
1 cm
3 cm
4 cm
The correct Answer is:A
To solve the problem, we need to determine the amplitude of oscillation of the two blocks connected by a spring after one of the blocks is given an initial velocity. Here’s a step-by-step solution:
Step 1: Understand the System
We have two blocks:
- Mass m1=1kg
- Mass m2=2kg
- Spring constant k=24N/m
- Initial velocity of m1, v0=12cm/s=0.12m
Step 2: Calculate the Reduced Mass
The reduced mass μ of the system can be calculated using the formula:
μ=m1m2m1+m2
Substituting the values:
μ=1×21+2=23kg
Step 3: Calculate the Initial Kinetic Energy
The initial kinetic energy (KE) of the system when m1 is given an initial velocity v0 is given by:
KE=12μv2
Substituting the values:
KE=12⋅23⋅(0.12)2
Calculating (0.12)2=0.0144:
KE=12⋅23⋅0.0144=13⋅0.0144=0.0048J
Step 4: Calculate the Maximum Potential Energy
At maximum compression of the spring, all the kinetic energy will convert into potential energy (PE) stored in the spring:
PE=12kx2
Setting KE=PE:
0.0048=12⋅24⋅x2
This simplifies to:
0.0048=12x2
Step 5: Solve for x
Rearranging gives:
x2=0.004812=0.0004
Taking the square root:
x=√0.0004=0.02m=2cm
Final Answer
The amplitude of oscillation is 2cm.
---
We have two blocks:
- Mass m1=1kg
- Mass m2=2kg
- Spring constant k=24N/m
- Initial velocity of m1, v0=12cm/s=0.12m
The reduced mass μ of the system can be calculated using the formula:
μ=m1m2m1+m2
Substituting the values:
μ=1×21+2=23kg
The initial kinetic energy (KE) of the system when m1 is given an initial velocity v0 is given by:
KE=12μv2
Substituting the values:
KE=12⋅23⋅(0.12)2
Calculating (0.12)2=0.0144:
KE=12⋅23⋅0.0144=13⋅0.0144=0.0048J
At maximum compression of the spring, all the kinetic energy will convert into potential energy (PE) stored in the spring:
PE=12kx2
Setting KE=PE:
0.0048=12⋅24⋅x2
This simplifies to:
0.0048=12x2
Rearranging gives:
x2=0.004812=0.0004
Taking the square root:
x=√0.0004=0.02m=2cm
The amplitude of oscillation is 2cm.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two bodies with masses m1 = 1kg and m2= 2kg are connected by a spring of force constant k=24Nm−1. The left ball is imparted an initial velocity v0=12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.
View SolutionTwo blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
View Solution
Knowledge Check
Two block of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impluse given a velocity of 14 m/s to the heavier block in the direction of the leghter block. The velocity of centre of mass is :
A30 m/sB20 m/sC10 m/sD5 m/sTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
A4 m/sB5m/sC2m/sD3m/sTwo blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is -
A30 m/sB20 m/sC10 m/sD5 m/s
Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
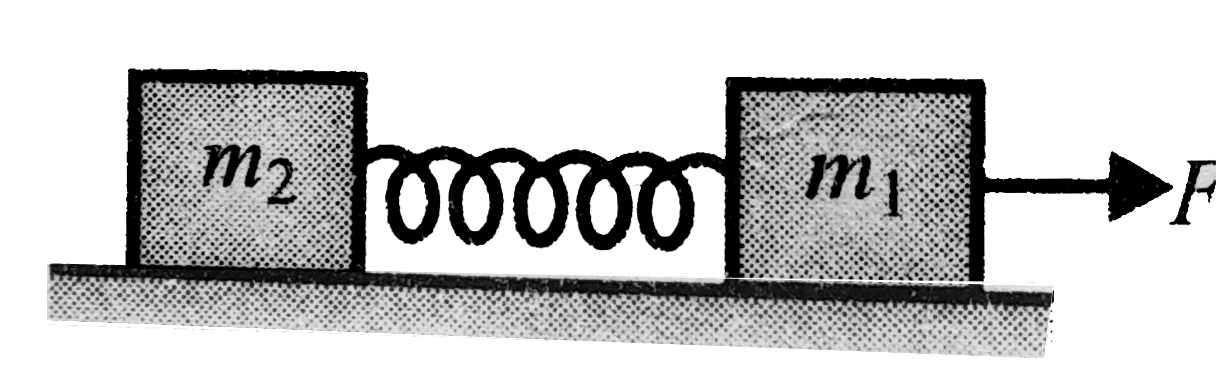
What is maximum elongation of spring.
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
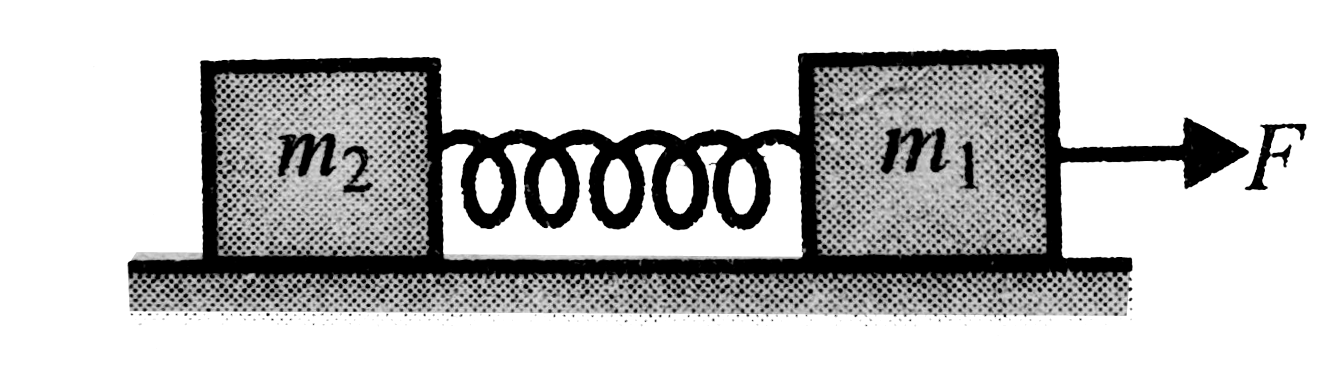
Which of the following statement is not true tn the watt of above system.
View Solution
