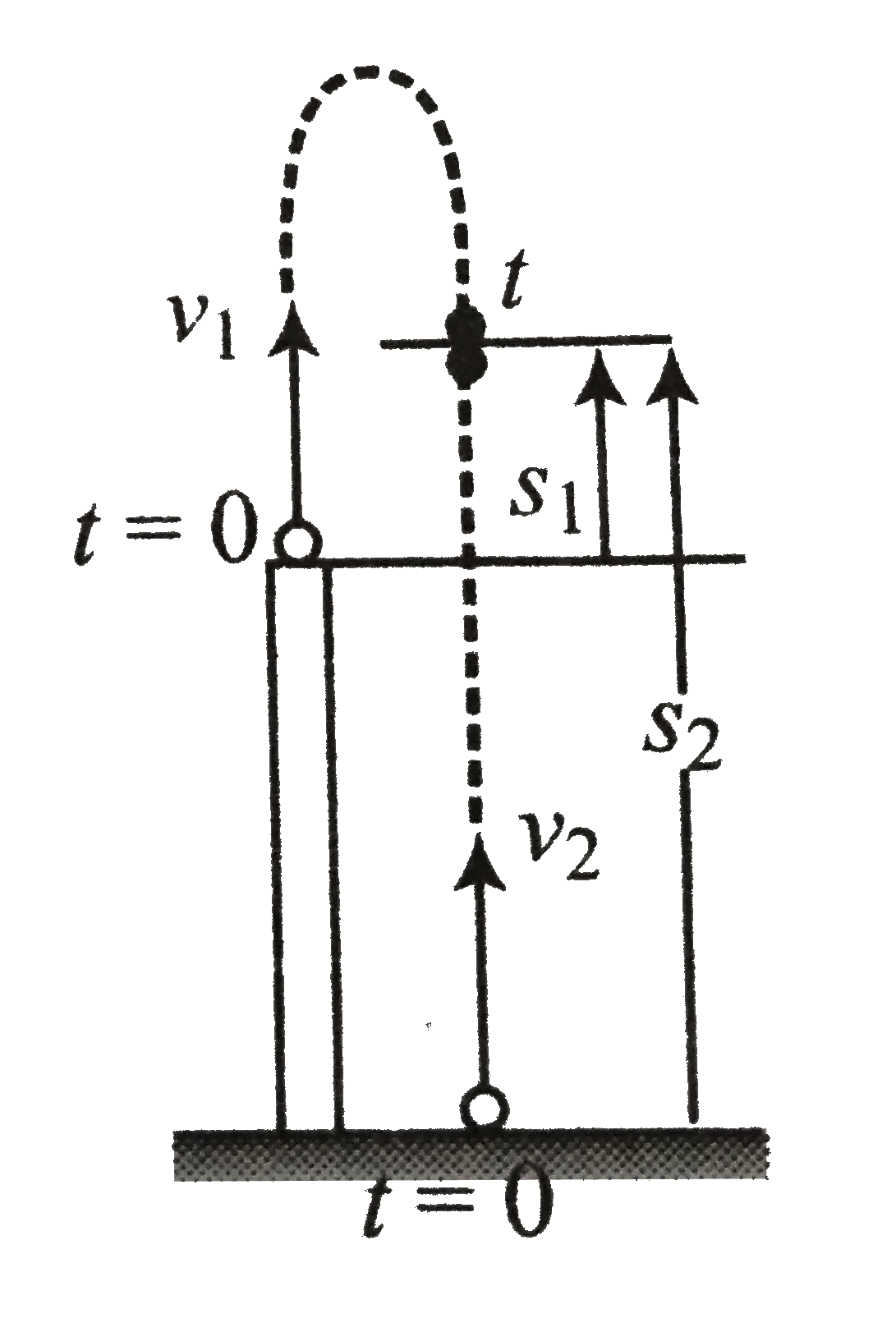
Two bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10 and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
The correct Answer is:5
Let the particle meet after a time t. First of all, we choose the
point of collision above the top of the cliff.
For the first particle, s=s1,v0=v1,a=−g
Then, s1=v1t−12gt2 .........(i)
For the second particle, s=s2,v0=v1,a=−g
Then , s2=v2t−12gt2 ..........(ii)
Referring to the figure, s2−s1=h......(iii)
Substtituting s1 from Eq. (i), s_2 from Eq. (ii) in Eq. (iii), we have
t=hv2−v1=104−2=5s.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Fill in the blanks
4 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
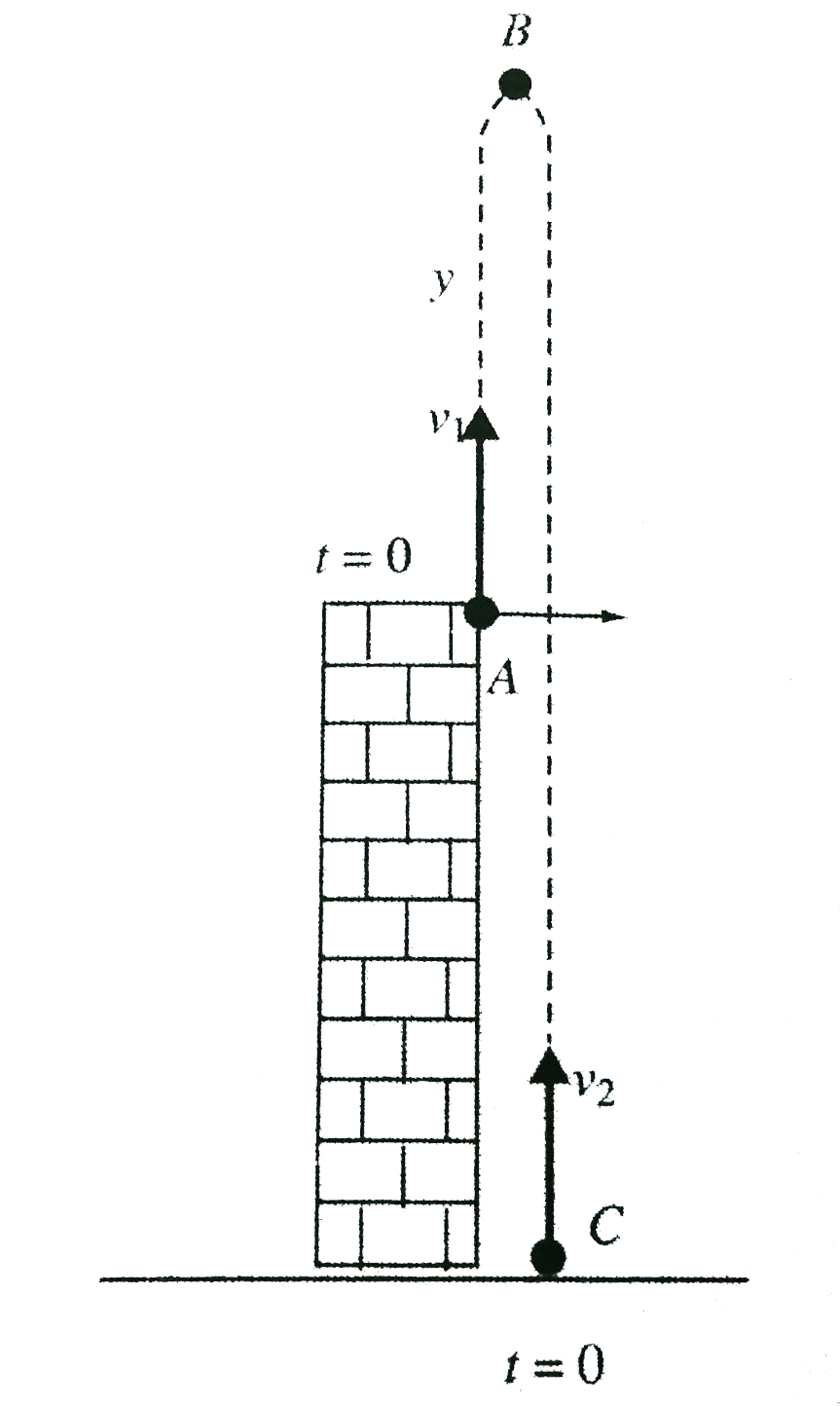
Two paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
View SolutionA ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A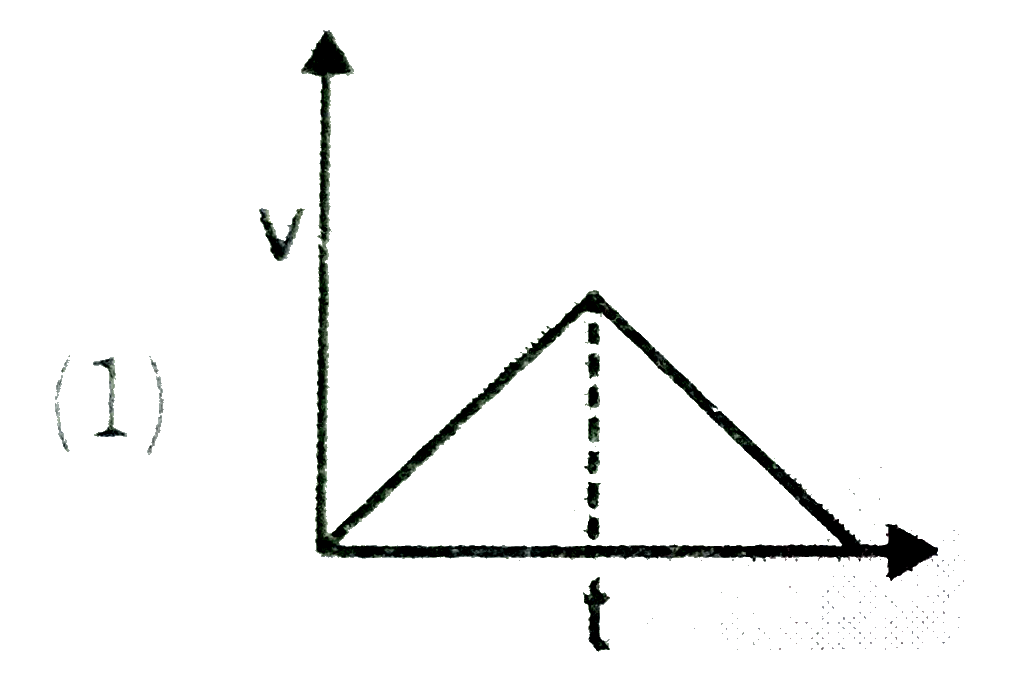 B
B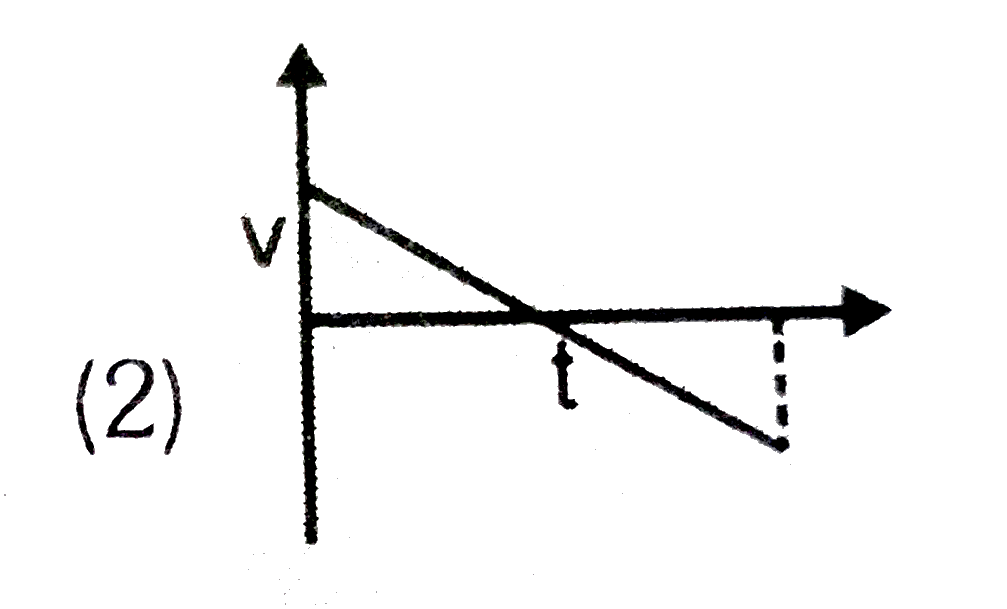 C
C D
D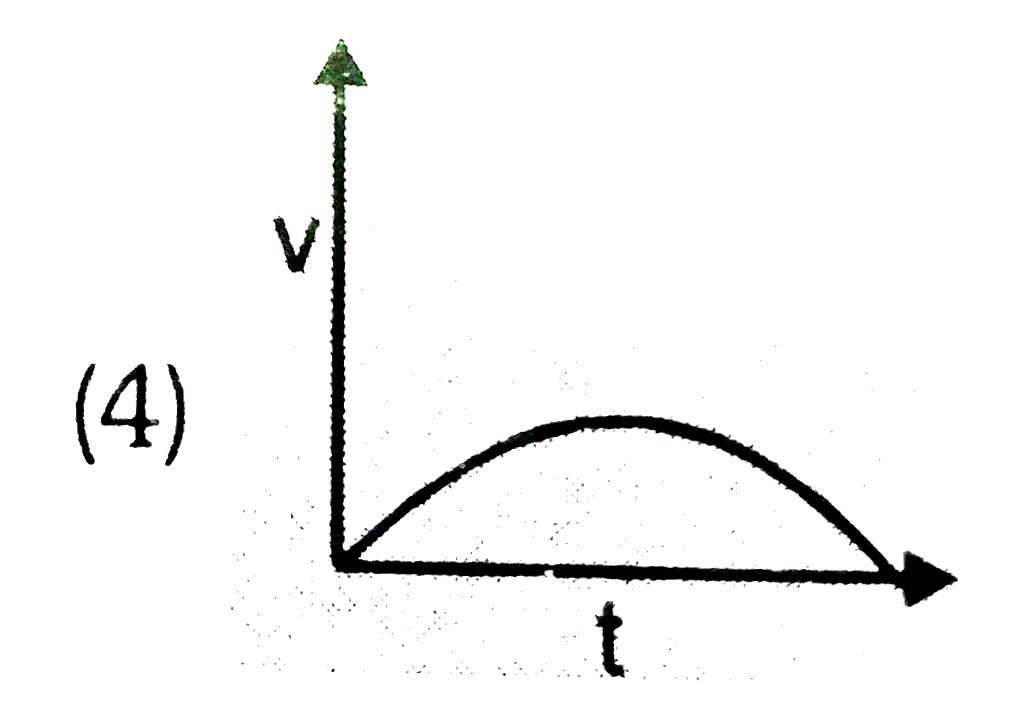
Displacement-time graph of a body projected vertically up is
Aa straight lineBa parabolaCa hyperbolaDa circleThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of 45∘ with the vertical, the escape velocity will be
A11√2kmsB22km/sC11km/sD11√2kms
A ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View SolutionA stone is released from the top of a cliff .Another particles is simultaneously projected v=10msec from the bottom of the cliff if they meet after 2 second find the height of the cliff.
View SolutionA body is projected horizontally from the top of a tower of height 10m with a velocity 10m/s .Its velocity after 1 second is
View SolutionDisplacement - time graph of a body projected vertically up is
View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of 45∘ with the vertical, the escape velocity will be
View Solution
