Two bodies of equal masses move with uniform velocities υand3υ respectively. Find the ratio of their kinetic energies.
The correct Answer is:A
To find the ratio of the kinetic energies of two bodies with equal masses moving at different velocities, we can follow these steps:
Step 1: Write the formula for kinetic energy
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
Step 2: Define the kinetic energies of both bodies
Let the mass of both bodies be m.
- For the first body moving with velocity v:
KE1=12mv2
- For the second body moving with velocity 3v:
KE2=12m(3v)2
Step 3: Simplify the kinetic energy of the second body
Now, simplify KE2:
KE2=12m(3v)2=12m(9v2)=92mv2
Step 4: Find the ratio of the kinetic energies
Now, we can find the ratio of the kinetic energies KE1 to KE2:
Ratio=KE1KE2=12mv292mv2
Step 5: Cancel out common terms
Since both kinetic energies have the same mass m and the common factor 12, we can cancel them out:
Ratio=19
Step 6: Write the final ratio
Thus, the ratio of the kinetic energies of the two bodies is:
Ratio=1:9
The kinetic energy (KE) of an object is given by the formula:
KE=12mv2
where m is the mass of the object and v is its velocity.
Let the mass of both bodies be m.
- For the first body moving with velocity v:
KE1=12mv2
KE2=12m(3v)2
Now, simplify KE2:
KE2=12m(3v)2=12m(9v2)=92mv2
Now, we can find the ratio of the kinetic energies KE1 to KE2:
Ratio=KE1KE2=12mv292mv2
Since both kinetic energies have the same mass m and the common factor 12, we can cancel them out:
Ratio=19
Thus, the ratio of the kinetic energies of the two bodies is:
Ratio=1:9
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Continuous Assessment24videos
WORK AND ENERGY
- BOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Assessment Through paper pen Test30videos
WORK AND ENERGY
- BOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Multiple choice Questions9videos
WORK AND ENERGY
- BOOK - PRADEEPCHAPTER - SOUNDEXERCISE - Model Test (sec - B)12videos
SOUND
Similar Questions
(a) Define the term 'energy' of a body. What is the SI unit of energy.
(b) What are the various from of energy ?
(c) Two bodies having equal masses are moving with uniform speeds fo v and 2v respectively. Find the ratio of their kinetic energies.View SolutionTwo objects having equal masses are moving with uniform velocities of 2 m/s and 6 m/s respectively. Calculate the ratio of their kinetic energies.
View Solution
Knowledge Check
- Question 1 - Select One
Two charged particles of charge +2q and +q have masses m and 2m respectively. Then are kept in uniform electric field allowed to move for the same time. Find the ratio of their kinetic energies.
A1:8B16:1C2:1D3:1 - Question 2 - Select One
Two bodies have their moments of inertia l and 2l respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A2:1B1:2C√2:1D1:√2 - Question 3 - Select One
Two bodies have their moments of inertia I and 2I, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A2:1B1:2C√2:1D1:√2
two bodies A and B of equal masses are kept at heights of h and 2h respectively. What will be the ratio of their potential energies ?
View SolutionTwo objects having same mass 'm' are moving with velocities v and 2v. Find ratio of their kinetic energies.
View SolutionTwo conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
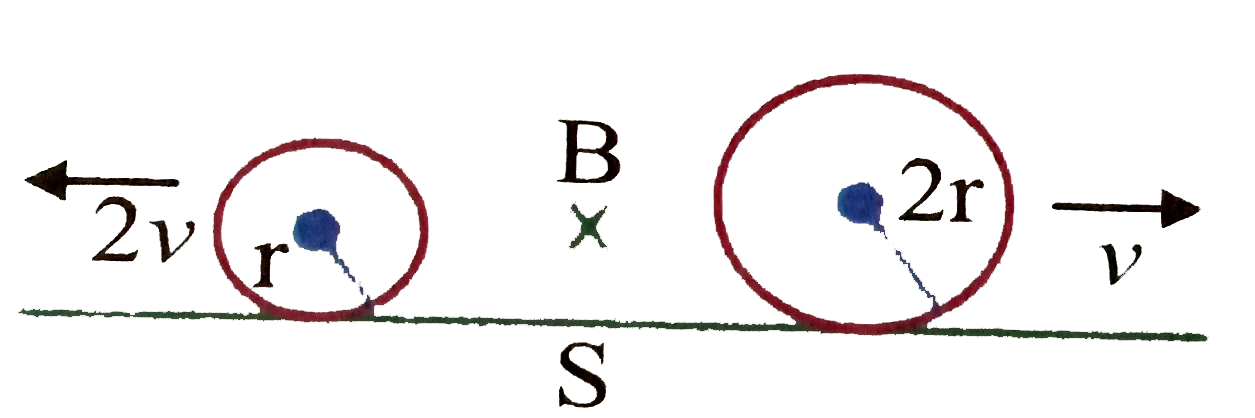 View Solution
View SolutionA plane wave of frquency ω propagates so that a certain phase of oscillation moves along the x,y,z axes with velocities υ1,υ2,υ3. Respectively. Find the wave vectork, assuming the unit vetors ex,ey,ez of the coordinate axes to be assigned.
View SolutionTwo bodies of masses 1 kg and 2kg have equal momentum. Then the ratio of their kinetic energies is
View Solution

