Two bodies of masses 0.1 kg and 0.4 kg move towards each other with the velocities 1 m/s and 0.1 m/s respectively, After collision they stick together. In 10 sec the combined mass travels
120 m
0.12 m
12 m
1.2 m
The correct Answer is:D
To solve the problem step by step, we will follow these procedures:
Step 1: Identify the masses and velocities of the two bodies.
- Mass of body 1 (m1) = 0.1 kg, Velocity of body 1 (v1) = 1 m/s (towards the right).
- Mass of body 2 (m2) = 0.4 kg, Velocity of body 2 (v2) = 0.1 m/s (towards the left).
Step 2: Calculate the initial momentum of both bodies.
- The momentum of body 1 (p1) = m1 * v1 = 0.1 kg * 1 m/s = 0.1 kg·m/s (to the right).
- The momentum of body 2 (p2) = m2 * v2 = 0.4 kg * (-0.1 m/s) = -0.04 kg·m/s (to the left).
Step 3: Calculate the total initial momentum of the system.
- Total initial momentum (P_initial) = p1 + p2 = 0.1 kg·m/s - 0.04 kg·m/s = 0.06 kg·m/s.
Step 4: Apply the conservation of momentum principle.
- After the collision, the two bodies stick together, so their combined mass (M) = m1 + m2 = 0.1 kg + 0.4 kg = 0.5 kg.
- Let the final velocity after collision be V.
- According to the conservation of momentum: P_initial = P_final
- Therefore, 0.06 kg·m/s = M * V = 0.5 kg * V.
Step 5: Solve for the final velocity (V).
- Rearranging gives: V = P_initial / M = 0.06 kg·m/s / 0.5 kg = 0.12 m/s.
Step 6: Calculate the distance traveled in 10 seconds.
- The distance (d) traveled by the combined mass after the collision can be calculated using the formula:
d=V×t
- Where V = 0.12 m/s and t = 10 seconds.
- Therefore, d = 0.12 m/s * 10 s = 1.2 meters.
Final Answer:
The combined mass travels a distance of 1.2 meters in 10 seconds.
---
- Mass of body 1 (m1) = 0.1 kg, Velocity of body 1 (v1) = 1 m/s (towards the right).
- Mass of body 2 (m2) = 0.4 kg, Velocity of body 2 (v2) = 0.1 m/s (towards the left).
- The momentum of body 1 (p1) = m1 * v1 = 0.1 kg * 1 m/s = 0.1 kg·m/s (to the right).
- The momentum of body 2 (p2) = m2 * v2 = 0.4 kg * (-0.1 m/s) = -0.04 kg·m/s (to the left).
- Total initial momentum (P_initial) = p1 + p2 = 0.1 kg·m/s - 0.04 kg·m/s = 0.06 kg·m/s.
- After the collision, the two bodies stick together, so their combined mass (M) = m1 + m2 = 0.1 kg + 0.4 kg = 0.5 kg.
- Let the final velocity after collision be V.
- According to the conservation of momentum: P_initial = P_final
- Therefore, 0.06 kg·m/s = M * V = 0.5 kg * V.
- Rearranging gives: V = P_initial / M = 0.06 kg·m/s / 0.5 kg = 0.12 m/s.
- The distance (d) traveled by the combined mass after the collision can be calculated using the formula:
d=V×t
- Where V = 0.12 m/s and t = 10 seconds.
- Therefore, d = 0.12 m/s * 10 s = 1.2 meters.
The combined mass travels a distance of 1.2 meters in 10 seconds.
Topper's Solved these Questions
Similar Questions
Two particles A and B of equal size but of masses m kg and 2 m kg are moving directly towards each other with speeds 21 m/s and 4 m/s respectively. After collision, A moves with a speed of 1 m/s in the original direction. Then:
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View Solution
Knowledge Check
- Question 1 - Select One
Two bodies of masses 5kg and 3kg are moving towards each other with 2ms−1 and 4ms−1 respectively. Then velocity of centre of mass is
A0.25ms−1 towards 3kgB0.5ms−1 towards 5kgC0.25ms−1 towards5kgD0.5ms−1 towards 3kg - Question 2 - Select One
Two balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
A15 m/sB10m/sC5 m/sD2.5 m/s - Question 3 - Select One
Two spheres of masses 1 kg and 2 kg are moving with velocities of 10 m/s and 5 m/s respectively in the same direction. After the collision the velocity of the lighter sphere decreases by 4 m/s. What is the coefficient of restitution?
A0.1B0.15C0.2D0.25
Two balls of masses 10 kg and 20 kg approach each other with velocities 30 m/s and 20 m/s respectively . Calculate their velocities after they undergo a perfectly eleastic collision .
View SolutionTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
View SolutionTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5 m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves (perfectly elastic collision)?
View SolutionTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
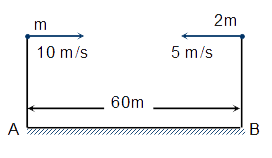 View Solution
View SolutionTwo bodeis A and B of masses 5.00 kg and 10.0 kg respectively moving in opposite directions with velocities 4.00 m/s and 0.50 m/s respectively make head-on collision in free space. The force of their mutual interaction varies according to the given graph. Select incorrect statement.
 View Solution
View Solution

