Two bodies of masses 4 kg and 6 kg connected by means of a light string are lying on a smooth horizontal surface. A horizontal pulling force is applied on the lighter body. Two seconds later the string connecting the two masses is cut. After two more seconds if the velocity of the heavier mass is 2ms−1, the force initially applied is
10N
25N
20N
40N
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have two bodies with masses m1=4kg and m2=6kg connected by a light string on a smooth horizontal surface. A horizontal force F is applied to the lighter mass m1.
Step 2: Determine the Acceleration
Since both masses are connected, they will accelerate together when the force F is applied. The total mass of the system is:
mtotal=m1+m2=4kg+6kg=10kg
The acceleration a of the system can be expressed as:
a=Fmtotal=F10
Step 3: Calculate the Velocity at t=2s
Using the formula for velocity:
v=u+at
where u is the initial velocity (which is 0), we can find the velocity of the heavier mass m2 at t=2s:
vm2(2)=0+(F10)⋅2=2F10=F5m/s
Step 4: Analyze the Situation After Cutting the String
At t=2s, the string is cut. After this point, the heavier mass m2 will continue to move with the velocity it had at t=2s since there is no force acting on it:
vm2(4)=vm2(2)=F5m/s
Step 5: Use the Given Information
We know that after two more seconds (at t=4s), the velocity of the heavier mass m2 is given as 2m/s:
F5=2
Step 6: Solve for the Force F
To find F, we can rearrange the equation:
F=2⋅5=10N
Final Answer
The force initially applied is F=10N.
---
We have two bodies with masses m1=4kg and m2=6kg connected by a light string on a smooth horizontal surface. A horizontal force F is applied to the lighter mass m1.
Since both masses are connected, they will accelerate together when the force F is applied. The total mass of the system is:
mtotal=m1+m2=4kg+6kg=10kg
The acceleration a of the system can be expressed as:
a=Fmtotal=F10
Using the formula for velocity:
v=u+at
where u is the initial velocity (which is 0), we can find the velocity of the heavier mass m2 at t=2s:
vm2(2)=0+(F10)⋅2=2F10=F5m/s
At t=2s, the string is cut. After this point, the heavier mass m2 will continue to move with the velocity it had at t=2s since there is no force acting on it:
vm2(4)=vm2(2)=F5m/s
We know that after two more seconds (at t=4s), the velocity of the heavier mass m2 is given as 2m/s:
F5=2
To find F, we can rearrange the equation:
F=2⋅5=10N
The force initially applied is F=10N.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Two masses 5kg and 2kg connected by a string are at rest on a smooth horizontal surface. A con stant force IN is applied on 5kg mass as shown in the figure. Two seconds later the string connecting the masses is cut but 'F' continues to act. After two more seconds

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400NTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks of mass 2 kg and 4 kg are kept in contact with each other on a smooth horizontal surface. A horizontal force of 12 N is applied on the first block due to which they move with certain constant acceleration. Calculate the force between the blocks.
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

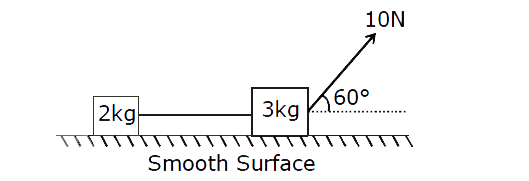
View SolutionFigure shows two blocks connected by a light inextensible string as shown in figure. A force of 10 N is applied on the bigger block at 60∘ with horizontal, then the tension in the st ring connection the two masses is -
View Solution
