The maximum tension a rope can withstand is 60 kg.wt. The ratio of maximum acceleration with which two boys of masses 20 kg and 30 kg can climb up the rope at the same time is
1:2
2:1
2:3
3:2
The correct Answer is:B
To solve the problem, we need to determine the ratio of maximum accelerations with which two boys of masses 20 kg and 30 kg can climb up a rope that can withstand a maximum tension of 60 kg.wt.
1. Convert Tension to Newtons:
The maximum tension that the rope can withstand is given as 60 kg.wt. We need to convert this to Newtons using the conversion factor 1 kg.wt=9.8 N.
T=60 kg.wt×9.8 N/kg=588 N
2. Identify Masses:
Let m1=20 kg (mass of the first boy) and m2=30 kg (mass of the second boy).
3. Apply Newton's Second Law for Each Boy:
For the first boy (mass m1):
T−m1g=m1a1
Rearranging gives:
a1=T−m1gm1
For the second boy (mass m2):
T−m2g=m2a2
Rearranging gives:
a2=T−m2gm2
4. Calculate Acceleration for Each Boy:
- For m1=20 kg:
a1=588 N−20 kg×9.8 N/kg20 kg=588−19620=39220=19.6 m/s2
- For m2=30 kg:
a2=588 N−30 kg×9.8 N/kg30 kg=588−29430=29430=9.8 m/s2
5. Calculate the Ratio of Accelerations:
Now, we find the ratio of the maximum accelerations:
Ratio=a1a2=19.69.8=2
Final Answer:
The ratio of maximum acceleration with which the two boys can climb up the rope is 2:1.
The maximum tension that the rope can withstand is given as 60 kg.wt. We need to convert this to Newtons using the conversion factor 1 kg.wt=9.8 N.
T=60 kg.wt×9.8 N/kg=588 N
Let m1=20 kg (mass of the first boy) and m2=30 kg (mass of the second boy).
For the first boy (mass m1):
T−m1g=m1a1
Rearranging gives:
a1=T−m1gm1
T−m2g=m2a2
Rearranging gives:
a2=T−m2gm2
- For m1=20 kg:
a1=588 N−20 kg×9.8 N/kg20 kg=588−19620=39220=19.6 m/s2
a2=588 N−30 kg×9.8 N/kg30 kg=588−29430=29430=9.8 m/s2
Now, we find the ratio of the maximum accelerations:
Ratio=a1a2=19.69.8=2
The ratio of maximum acceleration with which the two boys can climb up the rope is 2:1.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
View SolutionBlock B of mass 100 kg rests on a rough surface of friction coeffcient μ=1/3. A rope is tied to block B as shown in figure. The maximum acceleration with which boy A of 24 kg can climbs on rope without making block move is :
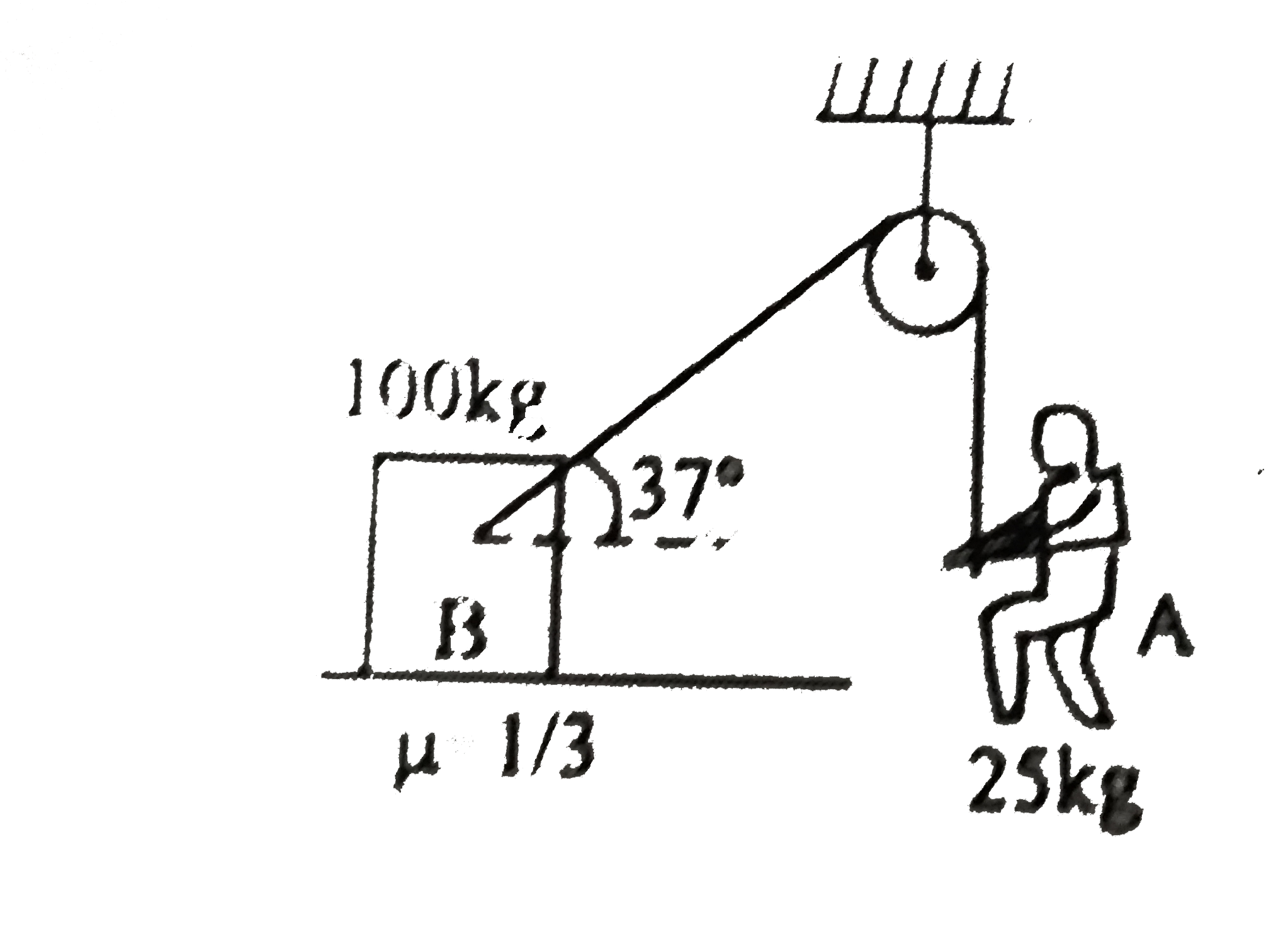
View SolutionA monkey of 25 kg is holding a vertical rope. The rope does not break if a body of mass less than 30 kg is suspended with the rope. What will be the maximum acceleration with which the monkey can climb up along the rope ? (Take g=10ms−2)
View SolutionA 24 kg block resting on a floor has a rope tied to its top. The maximum tension , the rope can withstand without breaking is 310 N . The minimum time in which the block can be lifted a vertical distance of 4.6 m by pulling on the rope is
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25kg is suspended from it but will break it the mass exeeds 25kg . What is the maximum acceleration with which the monkey can climb up along the rope? (g=10m/s2) .
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
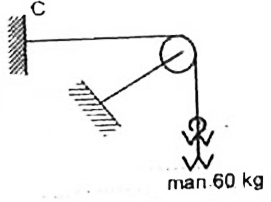
View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to fixed hook C, while the other end is free. Maximum tension that the rope can bear is 960 N. With what value of max. safe acceleration (m/s2) can a man of 60 kg climb on the rope?
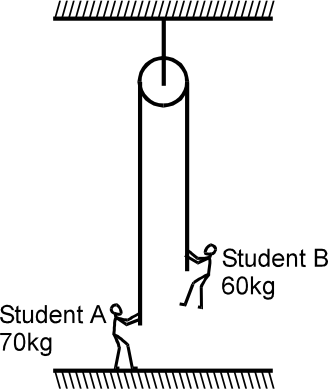
View SolutionA rope of negligible mass passes over a pulley of negligible mass attached to the ceiling, as shown in figure. One end of the rope is held by Student A of mass 70kg, who is at rest on the floor. The opposite end of the rope is held by Student B of mass 60kg, who is suspended at rest above the floor. The minimum acceleration a0 with which the Student B should climb up the rope to lift the Student A upward off the floor. (g=10m/s2)
View Solution