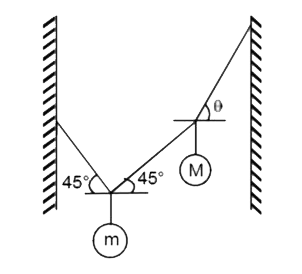
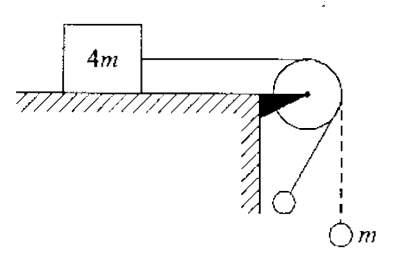
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
(2−cosθ03)
2cos2(θ02)
(1−cosθ02)
(3−2cosθ04)
The correct Answer is:D
Step by step video, text & image solution for Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude theta_(0) while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Knowledge Check
Two bodies of mass m and 4m are attached with string of length l is excurting oscillations of angular amplitude θ0 while the other body is at rest . The minimum coefficient of friction between the mass 4m and the horizontal surface should be:
 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)
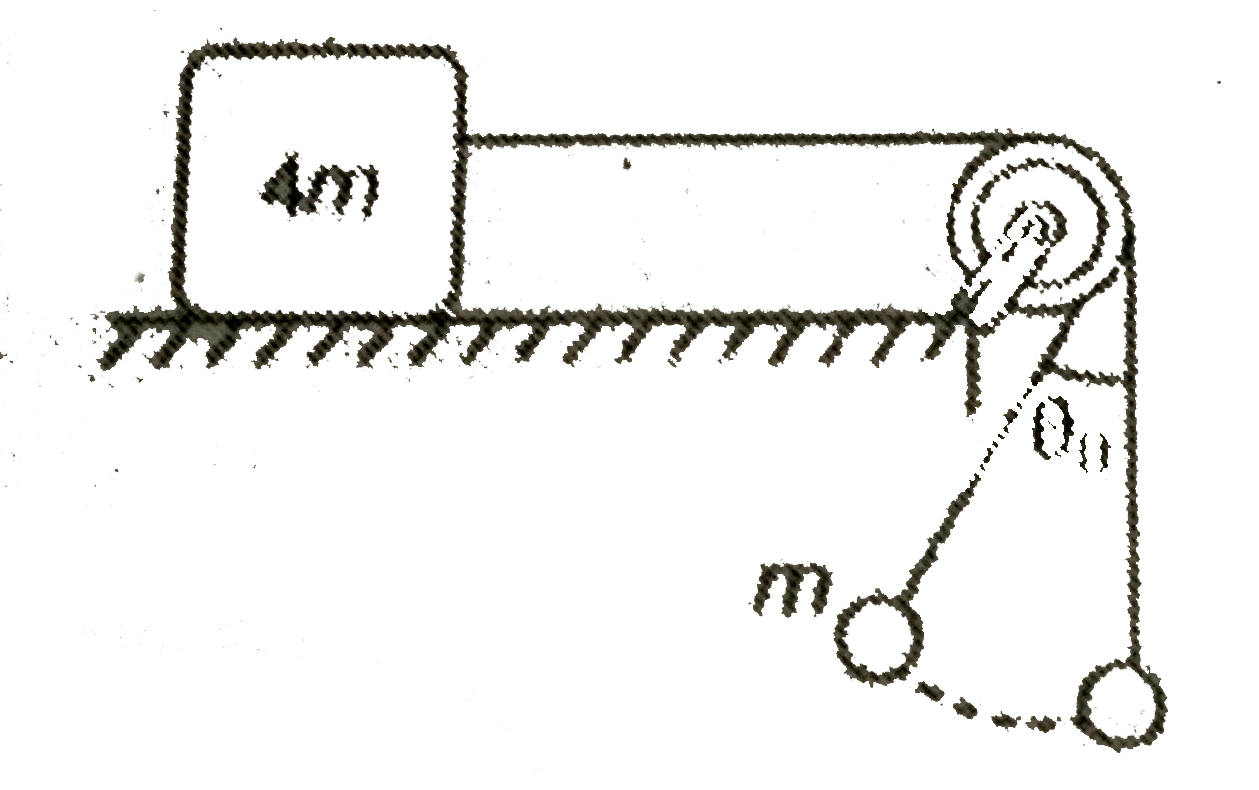
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−cosθ04)Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :
 A14(1−A2l2)B14(1+A2l2)C14AlcosθD14
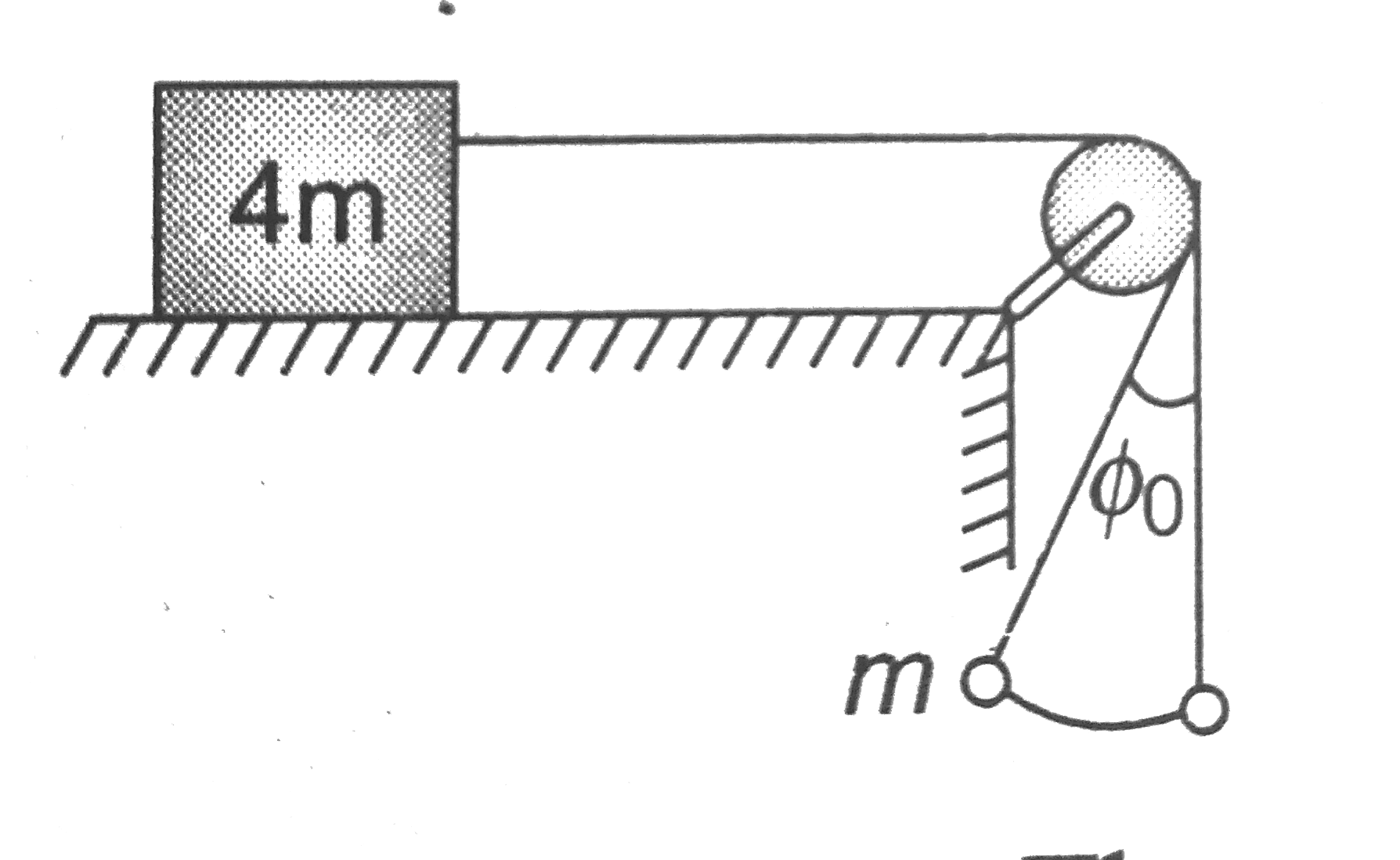
A14(1−A2l2)B14(1+A2l2)C14AlcosθD14Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
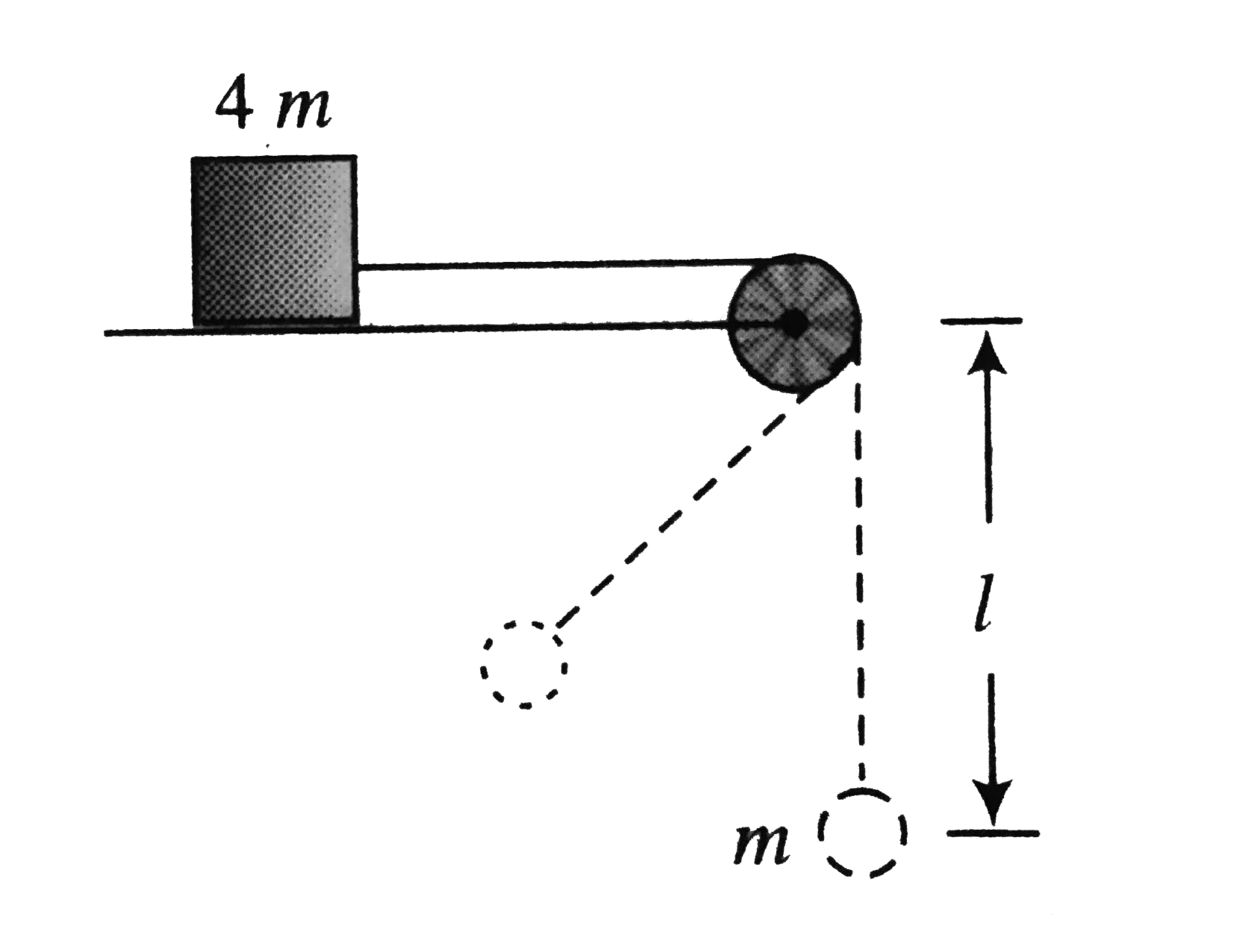 A(a) 14B(b) 34C(c) 12D(d) 18
A(a) 14B(b) 34C(c) 12D(d) 18
Two masses m1 and m2 are attached with light strings as shown. If the system is in equilibrium, find the value of θ
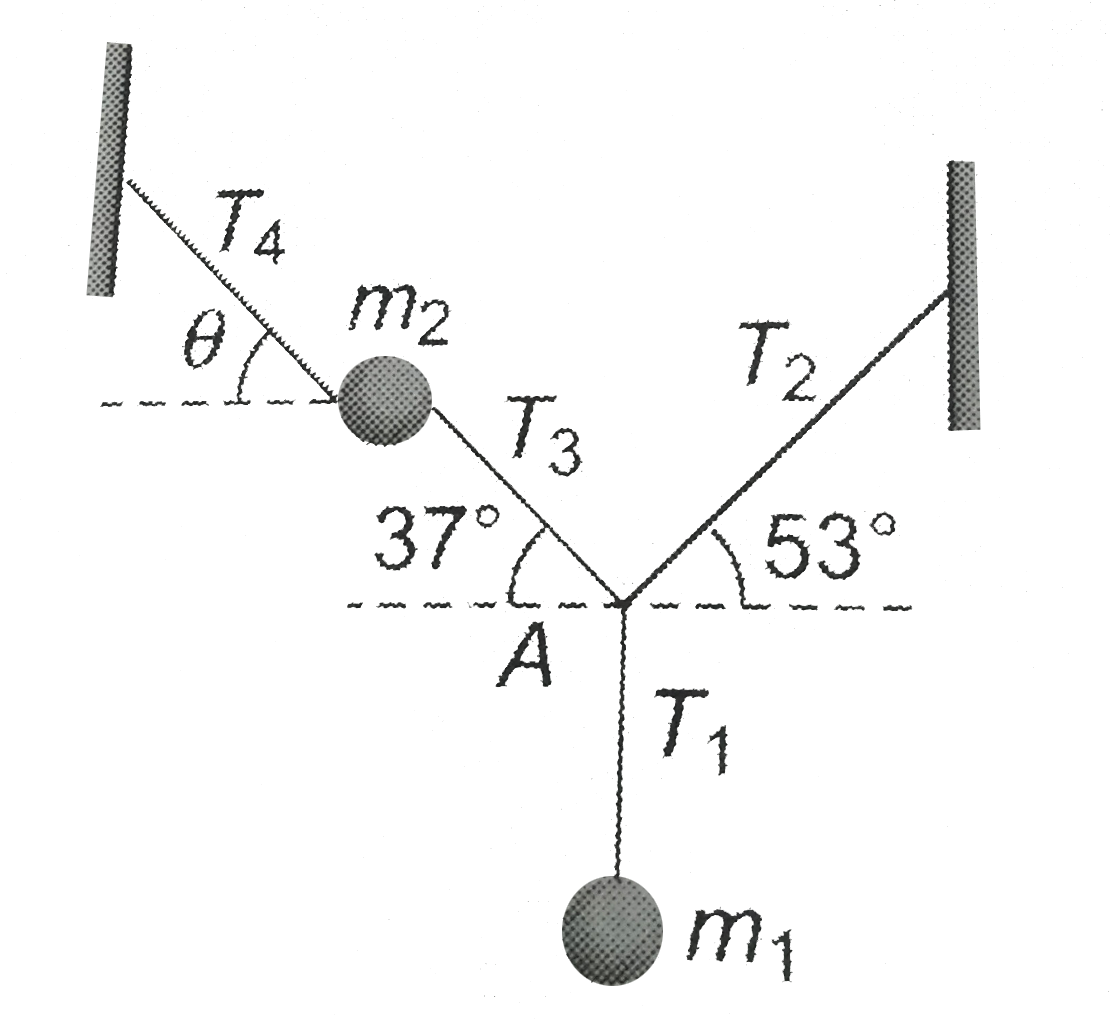
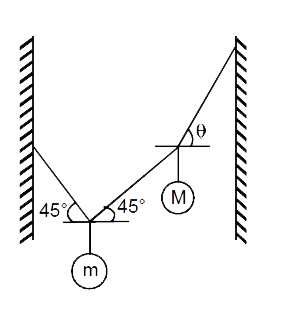
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View SolutionA uniform rod of mass m and length l is hanged by two stirngs as shown in figure. Suddenly one string is cut. The tension in other string at this instant is

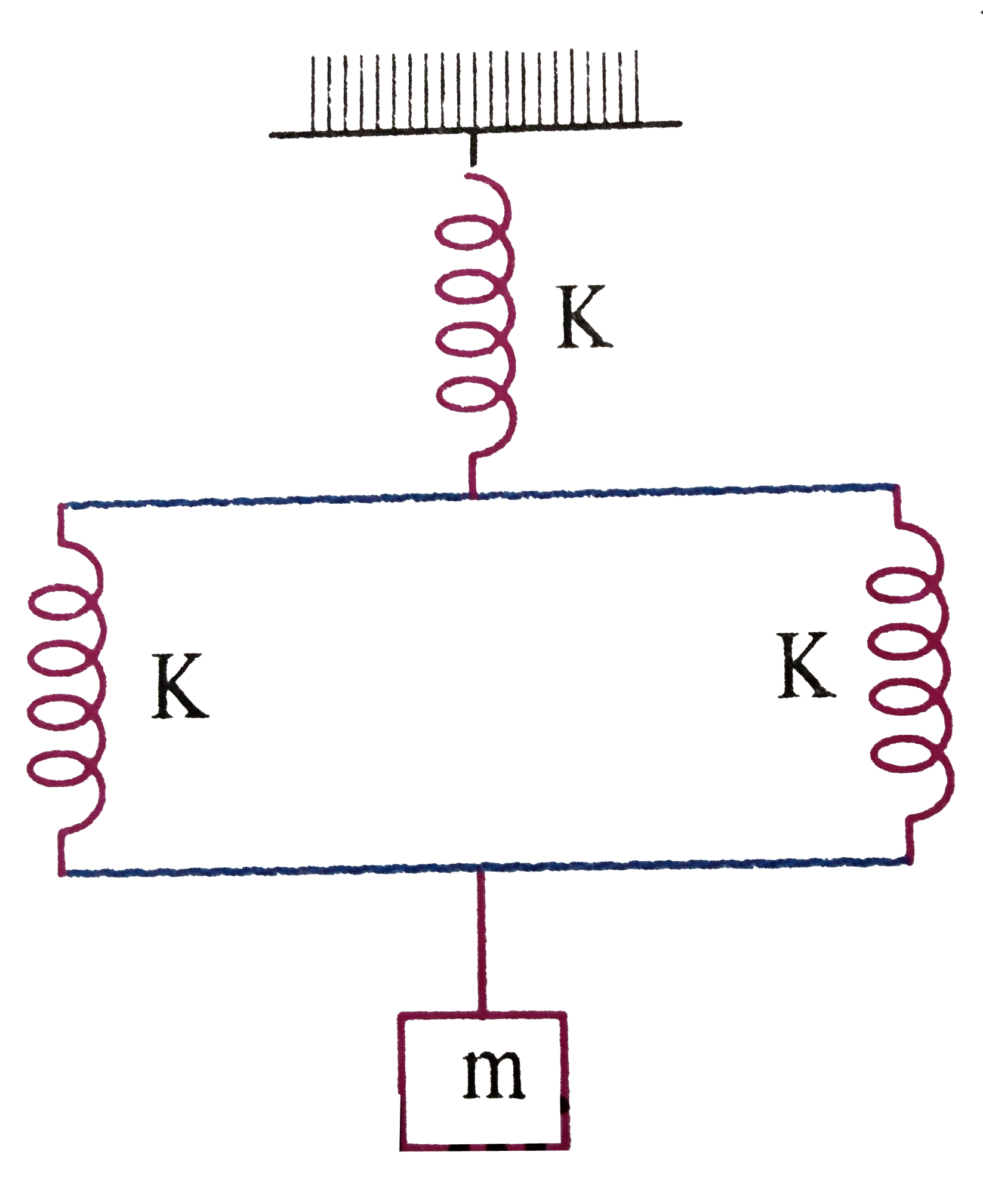
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
View SolutionA body of mass m and radius r is rotated with angular velocity ω as shown in the figure & kept on a surface that has sufficient friction then the body will move

View Solution