Two boys enter a running escalator at the ground floor in a shopping mall and they do some fun on it. The first boy repeatedly foolows step up and then steps down whereas the second body repeatedly follws steps up and then step down. Both of them move rlative to escalator with speed . If the first boy takes and the second boy takes the first boy takes to reach the first floor, how fast is escalator running ?.
To solve the problem, we need to analyze the movements of both boys on the escalator and set up equations based on their movements relative to the escalator.
Step 1: Define Variables
Let:
- v = speed of the escalator (in cm/s)
- vr=50 cm/s (relative speed of each boy with respect to the escalator)
- t1=250 s (time taken by the first boy)
- t2=50 s (time taken by the second boy)
Step 2: Analyze the First Boy's Movement
The first boy moves:
- Up: p1=1 step
- Down: q1=2 steps
In one complete cycle, he effectively moves:
- Up: 1 step
- Down: 2 steps
- Net movement in one cycle = 1−2=−1 step (downward)
Let the number of cycles he completes in t1 seconds be n1. The total time for one cycle is tc=(p1+q1)vr=(1+2)50=350 seconds.
The number of cycles n1 is:
n1=t1tc=250350=250×503=125003≈4166.67 cycles
Step 3: Calculate Effective Steps of the First Boy
The total effective steps taken by the first boy in t1 seconds:
Effective steps=n1×(−1)=−125003 steps
Step 4: Relate Steps to Distance
Let d be the height of the escalator in terms of steps. The effective distance moved by the first boy is:
d+v⋅t1=−125003
Where v⋅t1 is the distance moved by the escalator in t1 seconds.
Step 5: Analyze the Second Boy's Movement
The second boy moves:
- Up: p2=2 steps
- Down: q2=1 step
In one complete cycle, he effectively moves:
- Up: 2 steps
- Down: 1 step
- Net movement in one cycle = 2−1=1 step (upward)
Let the number of cycles he completes in t2 seconds be n2. The total time for one cycle is:
tc=(p2+q2)vr=(2+1)50=350 seconds
The number of cycles n2 is:
n2=t2tc=50350=50×503=25003≈833.33 cycles
Step 6: Calculate Effective Steps of the Second Boy
The total effective steps taken by the second boy in t2 seconds:
Effective steps=n2×1=25003 steps
Step 7: Relate Steps to Distance for the Second Boy
The effective distance moved by the second boy is:
d+v⋅t2=25003
Step 8: Set Up the Equations
Now we have two equations:
1. d+v⋅250=−125003
2. d+v⋅50=25003
Step 9: Solve the Equations
Subtract the second equation from the first:
(v⋅250−v⋅50)=−125003−25003
200v=−150003
v=−15000600=−25 cm/s
Since speed cannot be negative, the speed of the escalator is:
v=25 cm/s
Final Answer
The speed of the escalator is 25 cm/s.
---
Let:
- v = speed of the escalator (in cm/s)
- vr=50 cm/s (relative speed of each boy with respect to the escalator)
- t1=250 s (time taken by the first boy)
- t2=50 s (time taken by the second boy)
The first boy moves:
- Up: p1=1 step
- Down: q1=2 steps
- Up: 1 step
- Down: 2 steps
- Net movement in one cycle = 1−2=−1 step (downward)
n1=t1tc=250350=250×503=125003≈4166.67 cycles
The total effective steps taken by the first boy in t1 seconds:
Effective steps=n1×(−1)=−125003 steps
Let d be the height of the escalator in terms of steps. The effective distance moved by the first boy is:
d+v⋅t1=−125003
Where v⋅t1 is the distance moved by the escalator in t1 seconds.
The second boy moves:
- Up: p2=2 steps
- Down: q2=1 step
- Up: 2 steps
- Down: 1 step
- Net movement in one cycle = 2−1=1 step (upward)
tc=(p2+q2)vr=(2+1)50=350 seconds
n2=t2tc=50350=50×503=25003≈833.33 cycles
The total effective steps taken by the second boy in t2 seconds:
Effective steps=n2×1=25003 steps
The effective distance moved by the second boy is:
d+v⋅t2=25003
Now we have two equations:
1. d+v⋅250=−125003
2. d+v⋅50=25003
Subtract the second equation from the first:
(v⋅250−v⋅50)=−125003−25003
200v=−150003
v=−15000600=−25 cm/s
v=25 cm/s
The speed of the escalator is 25 cm/s.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.4
Explore 16 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Subjective
Explore 29 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.2
Explore 12 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
The first steps of SN1 and SN2 recatiosns are, respectively
View SolutionAt a metro station, a girl walks up a stationary escalator in time t1 If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up the moving escalator will be.
View Solution
Knowledge Check
In SN1 reaction, the first step involves the formation of:
Afree radicalBcarbanionCcarbocationDfinal productAt a metro station, a girl walks up a stationary escalator in time t1 If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up the moving escalator will be.
At1+t22Bt1t2t2−t1Ct1t2t1+t2Dt1−t2
At a metro station, a girl walks up a stationary escalator in time t1. If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be
View SolutionIn SN1 the first step involves the formation of
View SolutionA person climbs up a stalled escalator in 60s. If standing on the same but escalator running with constant velocity, he takes 40 s. How much time is taken by the person to walk up the moving escalator?
View SolutionA particle is thrown up vertically with a speed v1 in air . If takes time t1 in upward journey and t2(>t1) in the downward journey and returns to the starting point with a speed v2. Then:-
View SolutionA person decided to walk on an escalator which is moving at constant rate (speed). When he moves at the rate 1 step/sec. then he reaches top in 20 steps. Next day he goes 2 steps/sec. and reaches top in 32 steps. If speed of escalator is n steps/sec. Find the value of n
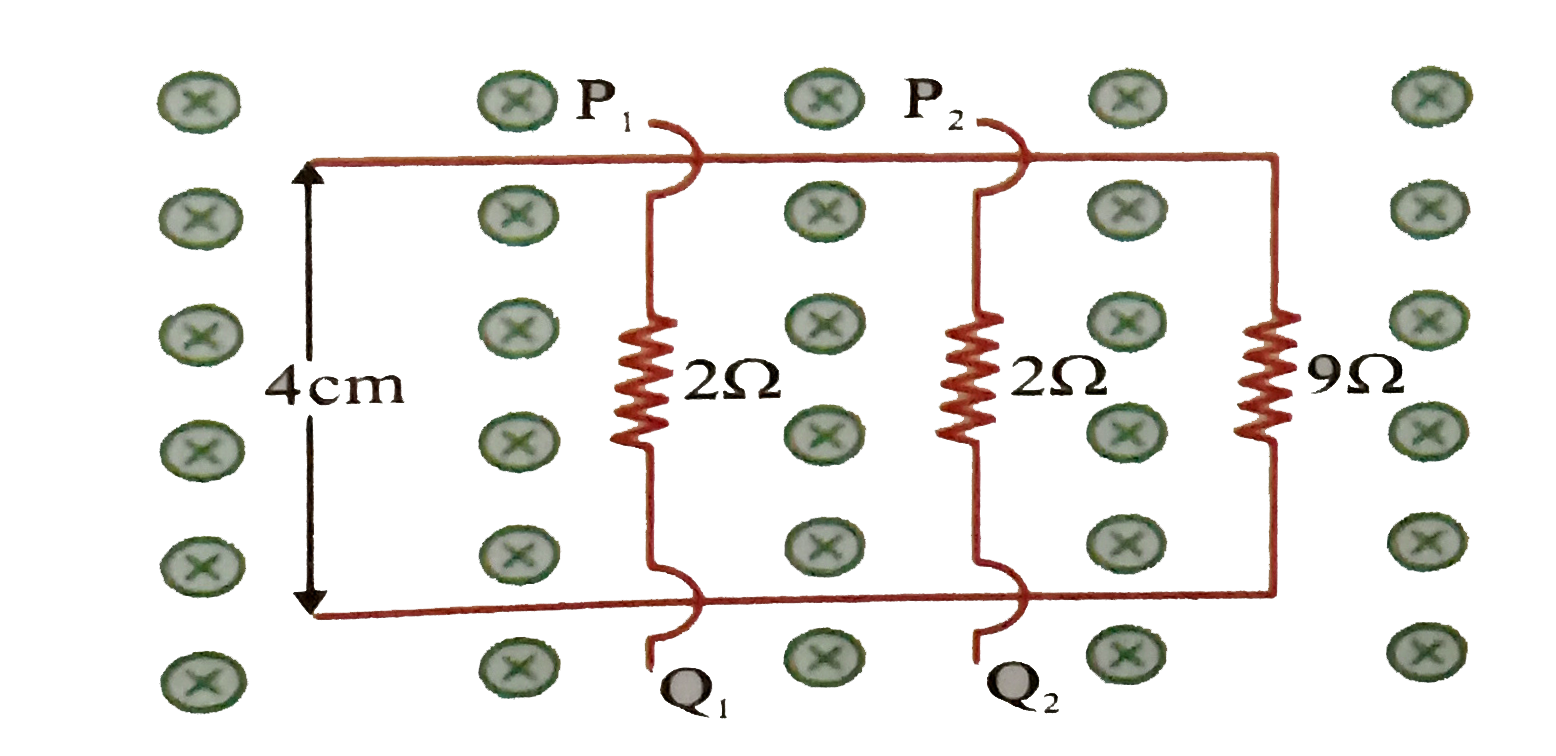
View SolutionIn the figure shown , the wires P1Q1 and P2Q2 are made to slide on the rails with same speed of 5cms−1. In this region a magnetic field of 1T exists. The electric current in the 9Ω resistance is :
View Solution