Two boys simultaneously aim their guns at a bird sitting on a tower. The first boy releases his shot with a speed of 100m/s at an angle of projection of 30∘ . The second boy is ahead of the first by a distance of 50 m and releases his shot with a speed of 80m/s. How must he aim his gun so that both the shots hit the bird simultaneously ? What is the distance of the foot of the tower from the two boys and the height of the tower ? With what velocities and when do the two shots hit the bird?
The correct Answer is:[θ−sin−1(58)]
To solve the problem step by step, we will analyze the projectile motion of both boys' shots and determine the required angle for the second boy to ensure both shots hit the bird simultaneously.
Step 1: Analyze the first boy's shot
The first boy shoots with a speed of u1=100m/s at an angle of θ1=30∘.
Horizontal and Vertical Components:
- Horizontal component:
u1x=u1cos(θ1)=100cos(30∘)=100×√32=50√3m/s
- Vertical component:
u1y=u1sin(θ1)=100sin(30∘)=100×12=50m/s
Step 2: Determine the time of flight for the first boy
The time of flight T can be calculated using the formula for the vertical motion:
h=u1yT−12gT2
where h is the height of the tower, and g is the acceleration due to gravity (approximately 9.81m/s2).
Step 3: Analyze the second boy's shot
The second boy is 50 m ahead and shoots with a speed of u2=80m/s at an angle θ2.
Horizontal and Vertical Components:
- Horizontal component:
u2x=u2cos(θ2)=80cos(θ2)m/s
- Vertical component:
u2y=u2sin(θ2)=80sin(θ2)m/s
Step 4: Set up the equations for horizontal motion
Both shots must hit the bird at the same time T. The horizontal distance traveled by both boys can be expressed as:
- For the first boy:
Distance=u1xT=50√3T
- For the second boy (who is 50 m ahead):
Distance=50+u2xT=50+80cos(θ2)T
Setting the distances equal gives:
50√3T=50+80cos(θ2)T
Step 5: Solve for θ2
Rearranging the equation:
50√3T−80cos(θ2)T=50
Factoring out T:
T(50√3−80cos(θ2))=50
Thus,
T=5050√3−80cos(θ2)
Step 6: Set up the equations for vertical motion
For the vertical motion, both projectiles must reach the same height h:
- For the first boy:
h=50T−12gT2
- For the second boy:
h=80sin(θ2)T−12gT2
Setting these equal gives:
50T−12gT2=80sin(θ2)T−12gT2
This simplifies to:
50T=80sin(θ2)T
Thus,
sin(θ2)=5080=58
Step 7: Find θ2
Using the inverse sine function:
θ2=sin−1(58)
Step 8: Calculate the height of the tower and the distance from the boys
Substituting T back into the height equation:
h=50T−12gT2
Using g≈9.81m/s2 and the value of T from earlier, we can find h.
Step 9: Determine the velocities when they hit the bird
The velocities can be calculated using:
- For the first boy:
v1=√u21x+(u1y−gT)2
- For the second boy:
v2=√u22x+(u2y−gT)2
Summary
1. The second boy must aim at an angle θ2=sin−1(58).
2. The height of the tower and the distance from the boys can be calculated using the derived equations.
The first boy shoots with a speed of u1=100m/s at an angle of θ1=30∘.
- Horizontal component:
u1x=u1cos(θ1)=100cos(30∘)=100×√32=50√3m/s
- Vertical component:
u1y=u1sin(θ1)=100sin(30∘)=100×12=50m/s
The time of flight T can be calculated using the formula for the vertical motion:
h=u1yT−12gT2
where h is the height of the tower, and g is the acceleration due to gravity (approximately 9.81m/s2).
The second boy is 50 m ahead and shoots with a speed of u2=80m/s at an angle θ2.
- Horizontal component:
u2x=u2cos(θ2)=80cos(θ2)m/s
- Vertical component:
u2y=u2sin(θ2)=80sin(θ2)m/s
Both shots must hit the bird at the same time T. The horizontal distance traveled by both boys can be expressed as:
- For the first boy:
Distance=u1xT=50√3T
- For the second boy (who is 50 m ahead):
Distance=50+u2xT=50+80cos(θ2)T
50√3T=50+80cos(θ2)T
Rearranging the equation:
50√3T−80cos(θ2)T=50
Factoring out T:
T(50√3−80cos(θ2))=50
Thus,
T=5050√3−80cos(θ2)
For the vertical motion, both projectiles must reach the same height h:
- For the first boy:
h=50T−12gT2
- For the second boy:
h=80sin(θ2)T−12gT2
50T−12gT2=80sin(θ2)T−12gT2
This simplifies to:
50T=80sin(θ2)T
Thus,
sin(θ2)=5080=58
Using the inverse sine function:
θ2=sin−1(58)
Substituting T back into the height equation:
h=50T−12gT2
Using g≈9.81m/s2 and the value of T from earlier, we can find h.
The velocities can be calculated using:
- For the first boy:
v1=√u21x+(u1y−gT)2
- For the second boy:
v2=√u22x+(u2y−gT)2
1. The second boy must aim at an angle θ2=sin−1(58).
2. The height of the tower and the distance from the boys can be calculated using the derived equations.
Topper's Solved these Questions
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Advance MCQs with One or More Options Correct
17 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
Similar Questions
Two persons simutaneously aim and fire their guns at a bird sitting on a tree. The first person fires his shot with a speed of 100m/s at an angle of projection of 30∘. The second person is ahead of the first by a distance of 50m and fire his shot with a speed of 80m/s. how must he aim his gun so that both the shots hit the bird simultaneously. Calculate the distance of the foot of the frre from two persons and the height of the tree. With what velocities and when do the two shorts hit the bird.
View SolutionA boy riding a bicycle covers a distance of 10 m in 40 s. What is the speed of the boy ?
View Solution
Knowledge Check
A hockey player receives a corner shot at a speed of 15m/s at an angle of 30∘ with the y-axis and then shoots the ball along the x-axis with a speed of 30m/s If the mass of the ball is 100gm and it remains in contact with the hockey stick for 0.01s, the force imparted to the ball in the x-direction is :
 A281.25 NB187.5NC562.5ND375 N
A281.25 NB187.5NC562.5ND375 NA boy is standing infront of a plane mirror at a distance of 3 m from it. What is the distance between the boy and his image
A3 mB6 mC4 . 5 mDnoneShots are fired from the top of a tower and from bottom simultaneously at angle 30∘ and 60∘ as shown. If horizontal distance of the point of collision is at a distance 'a' from the tower. Then height of tower h is
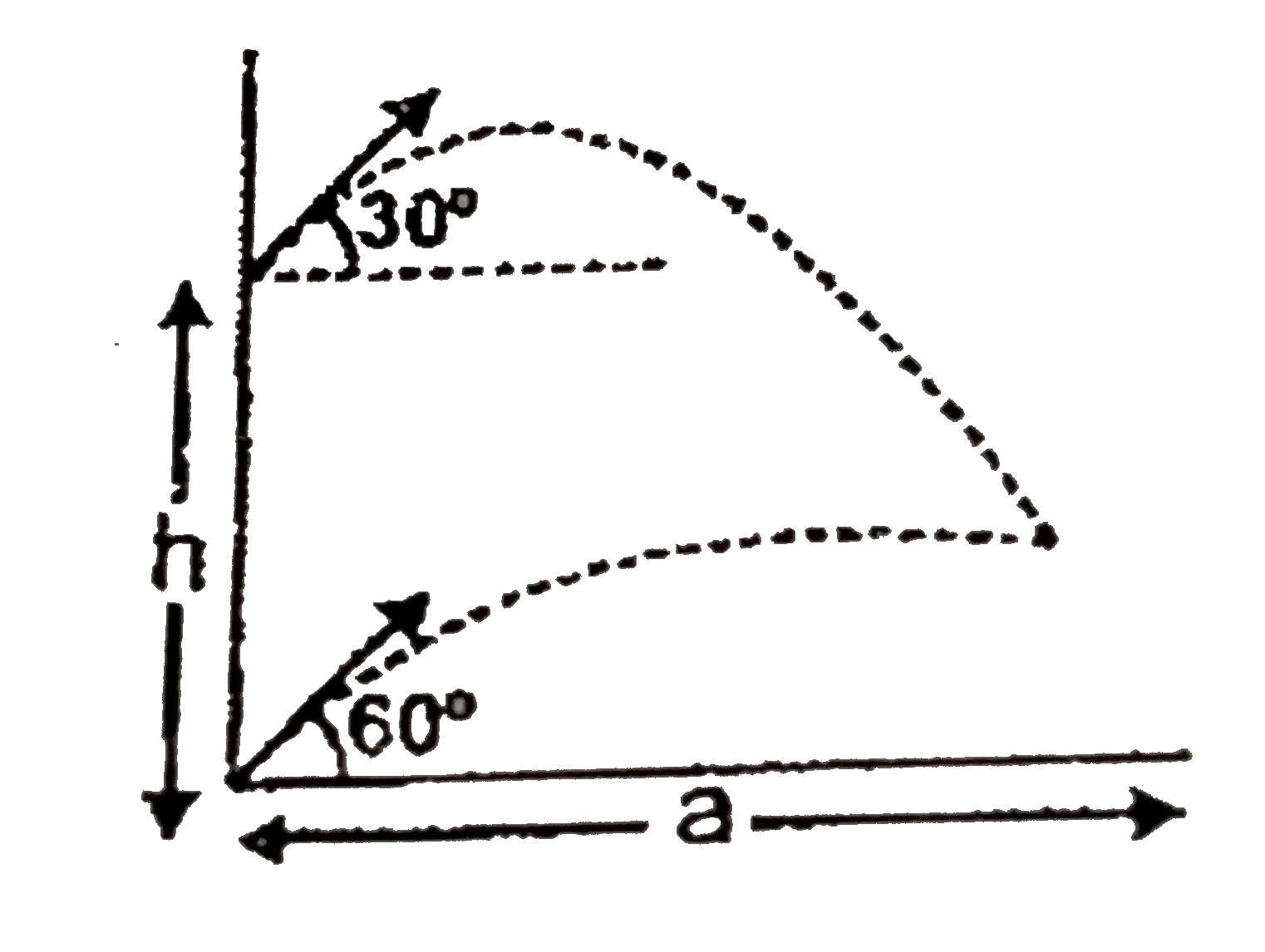 A2a√3Ba√3C2aD4a√3
A2a√3Ba√3C2aD4a√3
A boy hears an echo of his own voice from a distant hill after 1s. The speed of sound is 340m/s. What is the distance of the hill from the boy ?
View SolutionA boy went to his school at a speed of 12 km/hr and returned to his house at a speed of 8 km/hr. If he has taken 50 minutes for the whole journey, what was the total distance walked ?
View SolutionTo stand first in the class is his aim.
View SolutionA 50.0-kg boy runs at a speed of 10.0 m/s and jumps onto a cart as shown in the figure. The cart is initially at rest. If the speed of the cart with the boy on it is 2.50 m/s, what is the mass of the cart?

View SolutionA boy is standing in front of a plane mirror at a distance of 3 m from it. What is the distance between the boy and his image?
View Solution
