Two busses A and B are at positions 50m and 100m from the origin at time t=0. They start moving in the same direction simultaneously wi8th uniform velocities of and . Determine the time and position at which A overtakes B.
To solve the problem of when bus A overtakes bus B, we will follow these steps:
Step 1: Define the initial positions and velocities
- Let the initial position of bus A, SA(0)=50 m.
- Let the initial position of bus B, SB(0)=100 m.
- The velocity of bus A, VA=10 m/s.
- The velocity of bus B, VB=5 m/s.
Step 2: Write the equations of motion for both buses
The position of each bus as a function of time t can be expressed as:
- For bus A:
SA(t)=SA(0)+VA⋅t=50+10t
- For bus B:
SB(t)=SB(0)+VB⋅t=100+5t
Step 3: Set the positions equal to find the time of overtaking
To find the time t when bus A overtakes bus B, we set the two position equations equal to each other:
50+10t=100+5t
Step 4: Solve for t
Rearranging the equation gives:
10t−5t=100−50
5t=50
t=505=10 seconds
Step 5: Calculate the position at which A overtakes B
Now, we substitute t=10 seconds back into the equation for the position of bus A (or bus B, since they will be equal):
SA(10)=50+10⋅10=50+100=150 meters
Final Answer
Bus A overtakes bus B after 10 seconds at a position of 150 meters from the origin.
---
- Let the initial position of bus A, SA(0)=50 m.
- Let the initial position of bus B, SB(0)=100 m.
- The velocity of bus A, VA=10 m/s.
- The velocity of bus B, VB=5 m/s.
The position of each bus as a function of time t can be expressed as:
- For bus A:
SA(t)=SA(0)+VA⋅t=50+10t
- For bus B:
SB(t)=SB(0)+VB⋅t=100+5t
To find the time t when bus A overtakes bus B, we set the two position equations equal to each other:
50+10t=100+5t
Rearranging the equation gives:
10t−5t=100−50
5t=50
t=505=10 seconds
Now, we substitute t=10 seconds back into the equation for the position of bus A (or bus B, since they will be equal):
SA(10)=50+10⋅10=50+100=150 meters
Bus A overtakes bus B after 10 seconds at a position of 150 meters from the origin.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problem
19 Videos
- MOTION IN ONE DIMENSIONBOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66 Videos
- Motion in a PlaneBOOK - SL ARORACHAPTER - Motion in a PlaneEXERCISE - Excercise
397 Videos
- OSCILLATIONSBOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise
233 Videos
Similar Questions
Two buses AandB are at positions 60m 160 momtheorig∈attimet=0.They⋆tmov∈g∈thesamedirectionsiμ<a≠ouslywithuniformspeed54 km h^(-1)and36 km h^(-). Derermine the time and positiona t which AovertakenB.
View SolutionTwo cars (A) and (B) are at positions 100m and 200m from the origin at time t=0. They start simultaneously with velocities 10 ms^(-1) respectively. The car (A) will overtake the car (B) at a distance of .
View Solution
Knowledge Check
Two trains, each 50m long, are travelling in opposite directions with velocities 10ms−1and15ms−1. The time of their crossing each other is.
A2 sB4 sC2√3D4√3Two cars A and B are at rest at the origin O. If A starts with a uniform velocity of20m/s and B starts in the same direction with a constant acceleration of 2m/s2, then the cars will meet after time
A10sB20sC30sD40sBuses A and B are moving in the same direction with speed 20ms−1 and 15ms−1 respectively. Find the relative velcoity of A w.r.t. B and relative velocity of B w.r.t. A.
A(15ms−1)ˆi (−5ms−1)ˆiB(5ms−1)ˆi (−15ms−1)ˆiC(5ms−1)ˆi (−5ms−1)ˆiD(5ms−1)ˆi (15ms−1)ˆi
From the top of a tower of height H, identical bodies,A and B ,are thrown horizontally with velocities 100ms−1 and 50ms−1 in the same direction at the same instant. Then
View SolutionTwo bodies of masses 3 kg and 4 kg are moving along X axis. At a time t, the bodics are at a distance of 2 m and 3 m from the origin and has velocities of 2ms−1and−3ms−1. Calculate the position and velocity of centre of mass. What will be the total momentum of the system?
View SolutionA stone is dropped from a height of 100m .At the same instant another stone is projected vertically upwards with velocity of 50ms^(-1) .If g=10ms^(-2) ,the height from the ground at which the 2 stones meet is
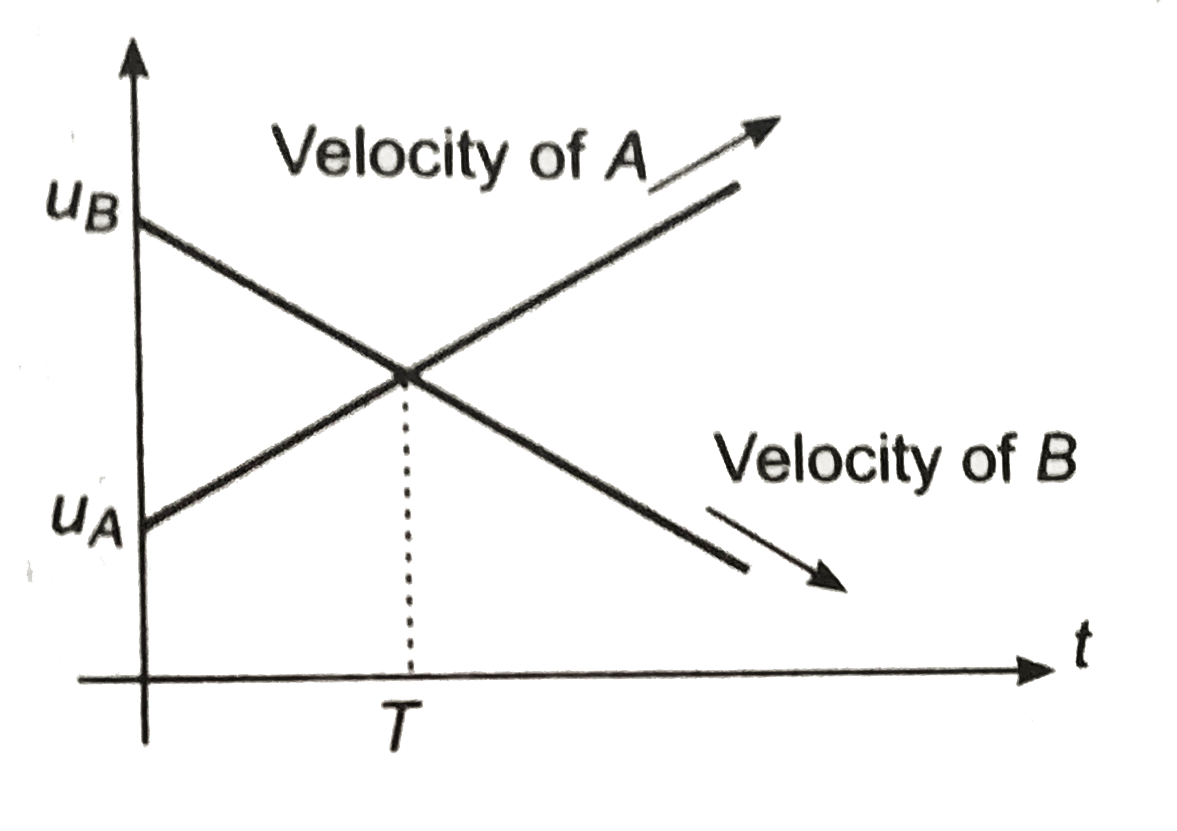
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if uA=6ms−1,uB=12ms−1 and at T velocity of A is 8ms−1andT=4s
View SolutionA body is moving along the +ve x-axis with uniform acceleration of −4ms−2. Its velocity at x=0 is 10ms−1. The time taken by the body to reach a point at x=12m is
View Solution
