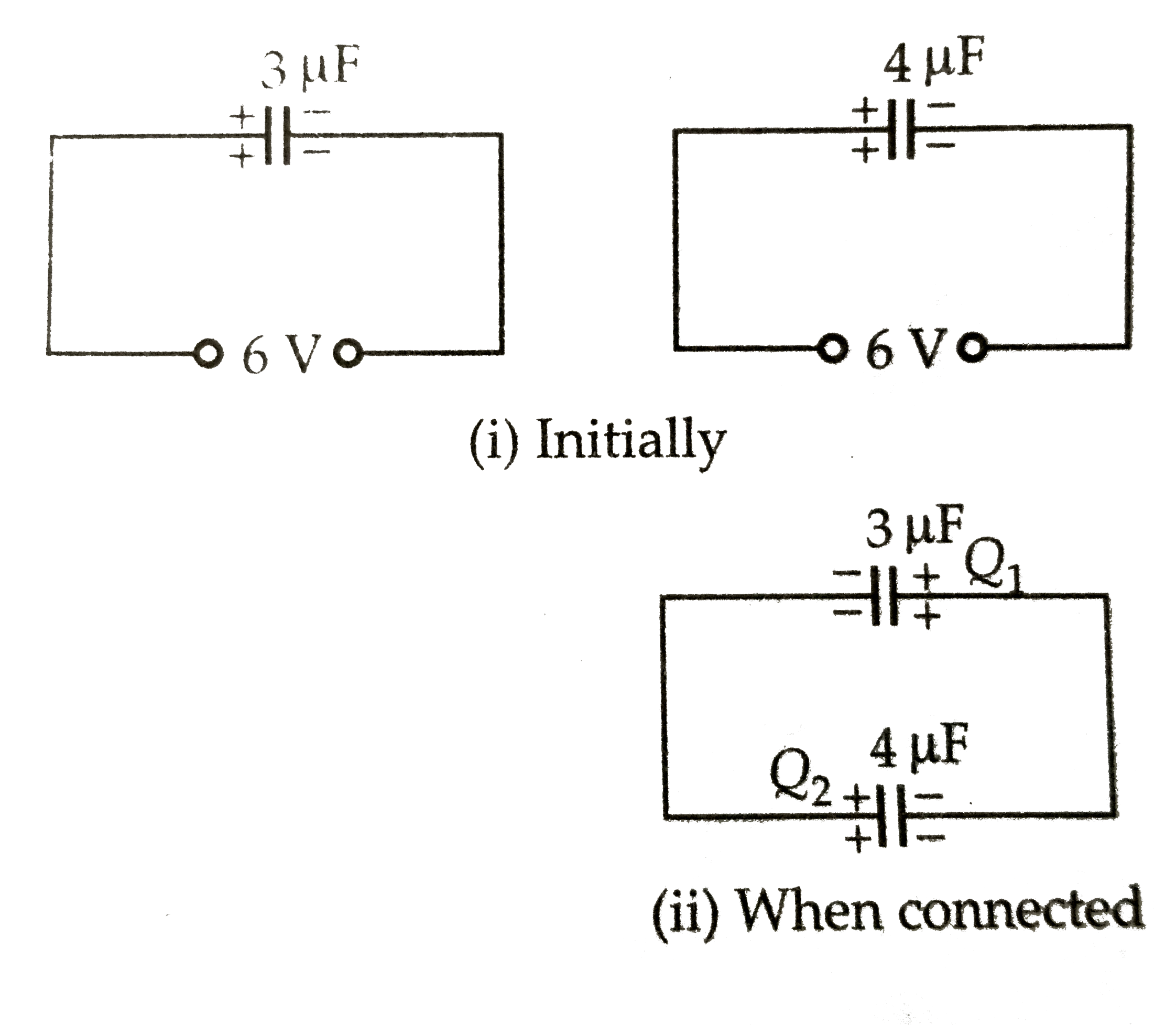
Two capcitors, 3 $μ F$ and $4 μ F,$ are individually charged across a 6 V battery. After being disconnected from the battery, they are connected together with the negative plate of one attached to the positive plate of the other. What is the final total energy stored ?

$1.26 \times 10^{- 4} J$

$2.57 \times 10^{- 4} J$

$1.25 \times 10^{- 6} J$

$2.57 \times 10^{- 6} J$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Two capacitors, $3 μ F$ and $4 μ F$ , are individually charged across a 6V battery. After being disconnected from the battery, they are connected together with the negative place of one attached to the positive plate of the other. What is the common potential?
A6V
B $(\frac{6}{7}) V$
C2V
D $(\frac{3}{2}) V$
A $5 μ F$ capacitor is fully charged across a 12 V battery, It is then disconnected from the battery and connected to an uncharged capacitor, If the voltage across the capacitor becomes 3 V then the capacitance of the
A $3 μ F$
B $15 μ F$
C $25 μ F$
D $60 μ F$
Two capacitors of capacitances $3 μ F$ and $6 μ F$ are charged to a potential of $12 V$ each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
A $6$ volt
B $4$ volt
C $3$ volt
DZero