Two cells, and of emfs 4 V and 8 V having internal resistances and respectively are connected in opposition to each other. This combination is connected in opposition to with resistance of and . Another resistance of is connected in parallel across the resistor. (a) Draw the circuit diagram (b) Calculate the total current flowing through the circuit. (c ) Terminal potential difference acrss cell and .
(a) The circuit diagram is shown in figure 
(b) As the resistance of and are in parallel, their effective resistance is
Total resistance of the circuit
Effective emf
Current
(c ) Here, cell E_(2)E_(1)epsilon_(1) +I r_(1) = 4 +0.5 xx 0.5 = 4.25 VE_(2)E_(2)=epsilon_(2) - I r_(2) = 8 -0.5 xx 1 = 7.5 V
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems3videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A7videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-29videos
COMMUNICATION SYSTEMS
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Two cells E1 and E2 of emfs 4 V and 8 V having internal resistances 0.5Ω and 1.0Ω respectively are connected in opposition to each other. This combination is connected in series with resistances of 4.5Ω and 3.0Ω. Another resistance is connected in parallel across the 3Ω resistor.
(a) Draw the circuit diagram
(b) Calculate the total current flowing through the circuit.View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View Solution
Knowledge Check
- Question 1 - Select One
Two batteries of emfs 2 V and 1 V of internal resistances 1Ωand2Ω respectively are connected in parallel. The effective emf of the combination is
A32VB53VC35VD2V - Question 2 - Select One
Two cells of e.m.f. 2.5 V and 2.0 V having internal resistance of 1Ω and 2Ω respectively are connected in parallel with similar poles connected together so as to send the current in the same direction through an external resistance of 2Ω. The current in the external resistance is
A0.87 AB1.29 AC1.00 AD2.29 A - Question 3 - Select One
If three resistors of resistance 2Ω,4Ω and 5Ω are connected in parallel then the total resistance of the combination will be
A2019ΩB1920ΩC1910ΩD1019Ω
Two cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionIn the circuit, the cells E1andE2 have emfs of 4V and 8V and internal resistance 0.5Ωand1.0Ω, respectively. Calculate the current through 6Ω resistance.
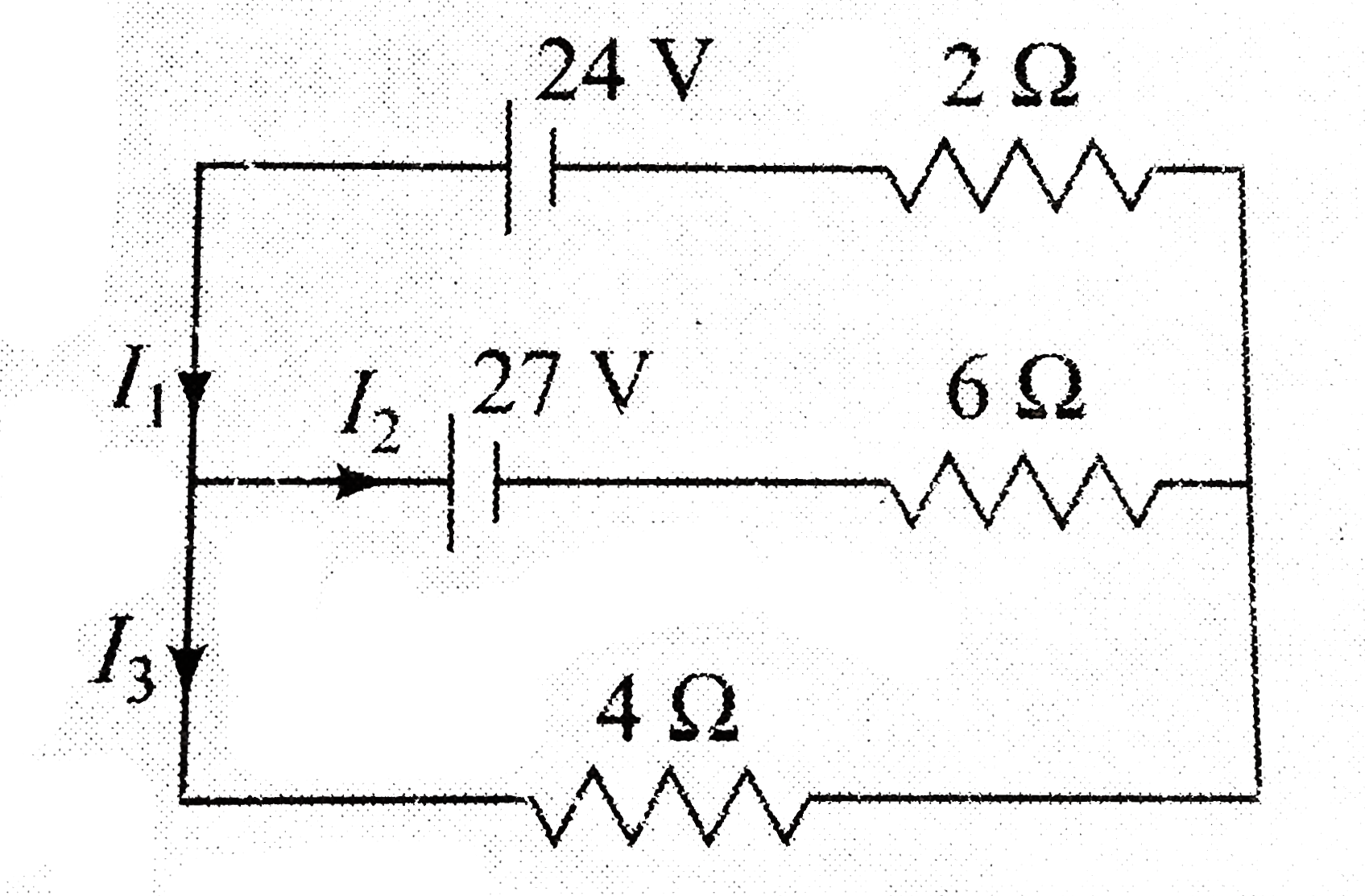 View Solution
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionTwo cells, of voltage 10 V and 2 V and internal resistances 10Ω and 5Ω respectively, are connected in parallel as shown in Fig. Find the effective voltage and effective resistance of the combination.
 View Solution
View SolutionTwo cells E1 and E2 in the circuit shown in figure, have emfs of 5 V and 9 V and internal resistance of 0.3Ω and 1.2Ω respestivley. Calculate the value of current flowing through the resistance of 3Ω.
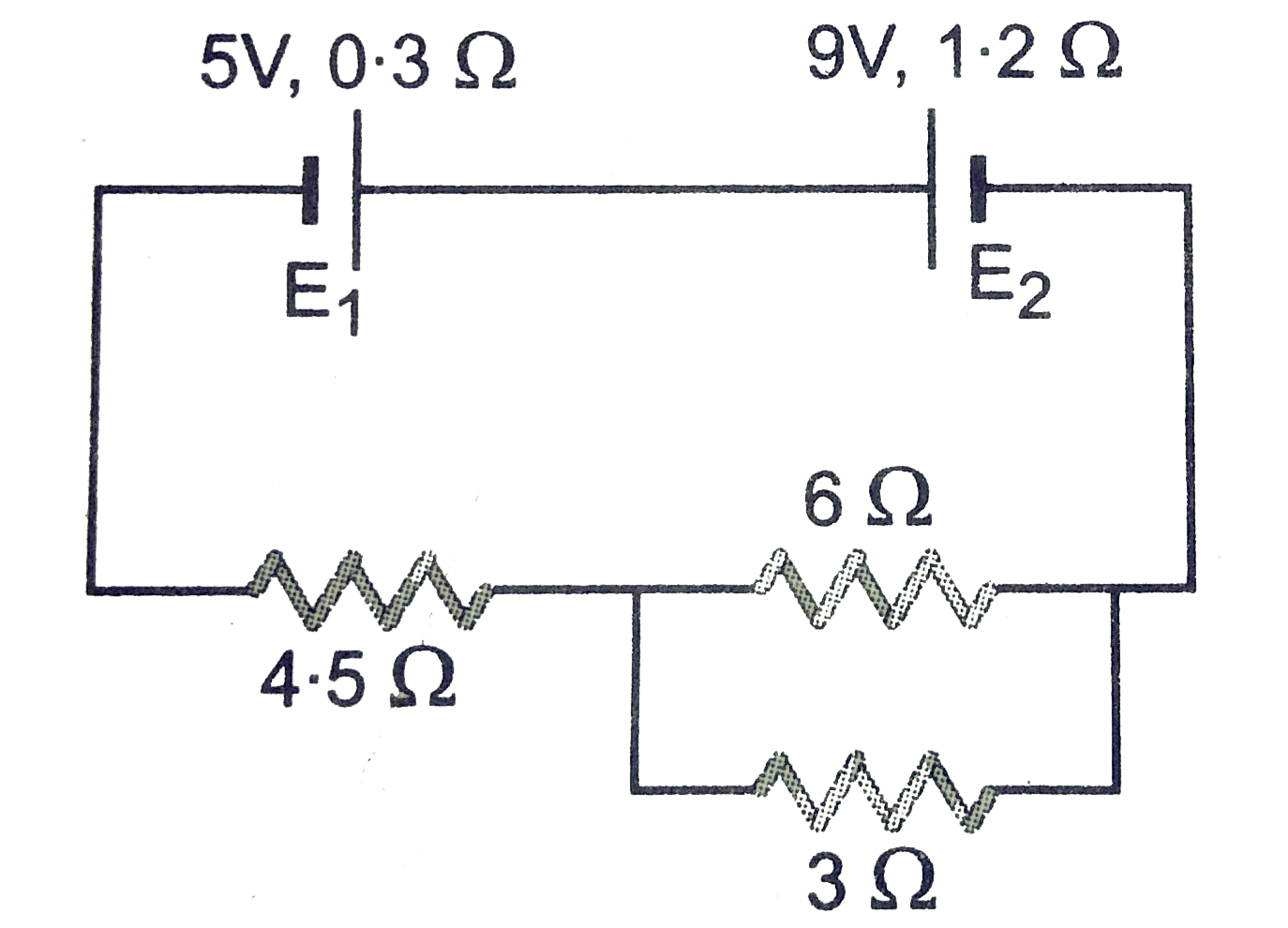 View Solution
View Solution

