Two charges, each of −q, are fixed and separated by a distance 2d. A third charge q of mass m is placed at the mid-point of the two fixed charges. q is displaced slightly by x(x⟨), perpendicular to the line joining the two fixed charged as shown in the figure. q will perform simple harmonic oscillation if the time period of (SHM) is T=απ3ɛ0md3q2][12). Find α
'(##CEN_KSR_PHY_JEE_C18_E01_013_Q04##)'
The correct Answer is:8
To solve the problem, we need to analyze the forces acting on the charge q when it is displaced slightly from its equilibrium position. The two fixed charges −q will exert forces on the charge q, and we can derive the conditions for simple harmonic motion (SHM) from these forces.
1. Understanding the Setup:
- We have two fixed charges, each of −q, separated by a distance 2d.
- A third charge q is placed at the midpoint of the two fixed charges.
- When the charge q is displaced by a small distance y (perpendicular to the line joining the two fixed charges), we need to find the restoring force acting on it.
2. Calculating the Forces:
- The force F due to one of the fixed charges on the charge q is given by Coulomb's law:
F=k(−q)(q)r2
- Here, r is the distance from the charge q to one of the fixed charges. When q is displaced by y, the distance r can be approximated as:
r=√d2+y2
- The total force Fnet on charge q due to both fixed charges will be the vector sum of the forces due to each charge.
3. Finding the Net Force:
- The net force acting on q when displaced by y can be expressed as:
Fnet=2Fcos(θ)
- For small angles, cos(θ)≈1, and hence:
Fnet≈2F=2(kq2(d2+y2))
- The restoring force (which acts in the opposite direction of the displacement) can be approximated as:
Frestoring=−2kq2y(d2+y2)3/2
4. Simplifying the Expression:
- For small displacements (y≪d), we can approximate (d2+y2)3/2≈d3:
Frestoring≈−2kq2yd3
5. Relating to SHM:
- The force can be related to the acceleration:
F=ma=−k′y
- Here, k′=2kq2d3. Thus, we can express the time period T of SHM as:
T=2π√mk′=2π√md32kq2
6. Substituting for k:
- Recall that k=14πε0:
T=2π
⎷md32(14πε0)q2=2π√4πε0md32q2=2π√8πε0md3q2
7. Identifying α:
- Comparing this with the given expression for T:
T=(απ3ε0md3q2)1/2
- We find that α=8.
Final Answer
Thus, the value of α is 8.
- We have two fixed charges, each of −q, separated by a distance 2d.
- A third charge q is placed at the midpoint of the two fixed charges.
- When the charge q is displaced by a small distance y (perpendicular to the line joining the two fixed charges), we need to find the restoring force acting on it.
- The force F due to one of the fixed charges on the charge q is given by Coulomb's law:
F=k(−q)(q)r2
- Here, r is the distance from the charge q to one of the fixed charges. When q is displaced by y, the distance r can be approximated as:
r=√d2+y2
- The total force Fnet on charge q due to both fixed charges will be the vector sum of the forces due to each charge.
- The net force acting on q when displaced by y can be expressed as:
Fnet=2Fcos(θ)
- For small angles, cos(θ)≈1, and hence:
Fnet≈2F=2(kq2(d2+y2))
- The restoring force (which acts in the opposite direction of the displacement) can be approximated as:
Frestoring=−2kq2y(d2+y2)3/2
- For small displacements (y≪d), we can approximate (d2+y2)3/2≈d3:
Frestoring≈−2kq2yd3
- The force can be related to the acceleration:
F=ma=−k′y
- Here, k′=2kq2d3. Thus, we can express the time period T of SHM as:
T=2π√mk′=2π√md32kq2
- Recall that k=14πε0:
T=2π
⎷md32(14πε0)q2=2π√4πε0md32q2=2π√8πε0md3q2
- Comparing this with the given expression for T:
T=(απ3ε0md3q2)1/2
- We find that α=8.
Thus, the value of α is 8.
Topper's Solved these Questions
Similar Questions
Two charges, each of −q, are fixed and separated by a distance 2d. A third charge q of mass m is placed at the mid-point of the two fixed charges. q is displaced slightly by x(x⟨), perpendicular to the line joining the two fixed charged as shown in the figure. q will perform simple harmonic oscillation if the time period of (SHM) is T=απ3ɛ0md3q2][12). Find α
'(##CEN_KSR_PHY_JEE_C18_E01_013_Q04##)'
View SolutionTwo positive point charges , each Q , are fixed at separation d. A third charge q is placed in the middle. Describe the equilibrium of the third charge.
View Solution
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
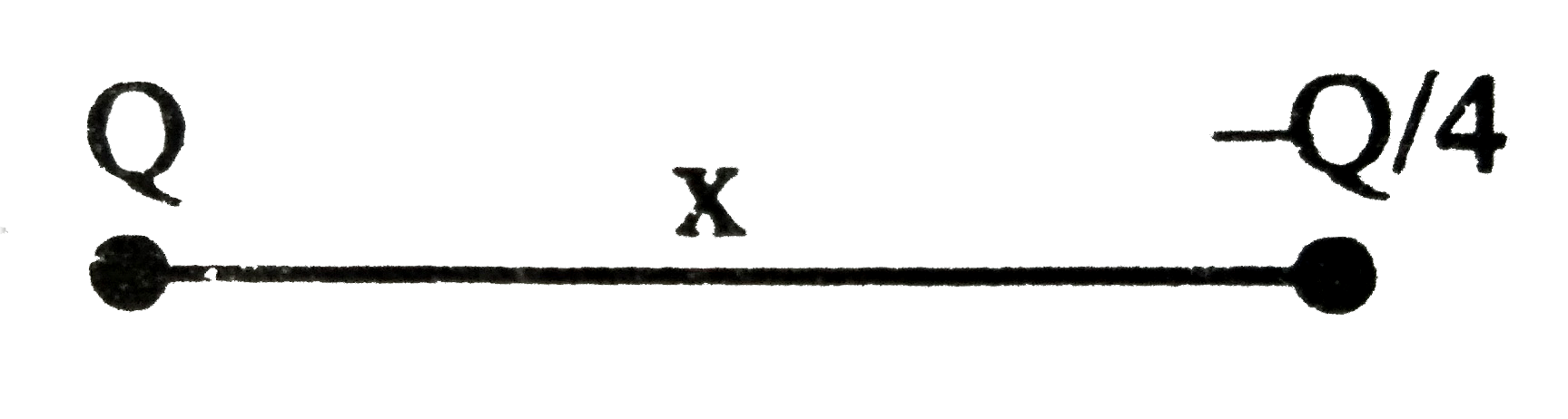 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
Ad2(1+√3) to the left of qBd2(1+√3) tothe right of qCd2(1+√5) to the left of qDd2(1+√5) to the right of qTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
Aincrease if Q is slightly displaced along x-axisBdecrease if Q is slightly displaced along x-axisCincrease if Q is slightly displaced along y-axisDdecrease if Q is slightly displaced along y-axis
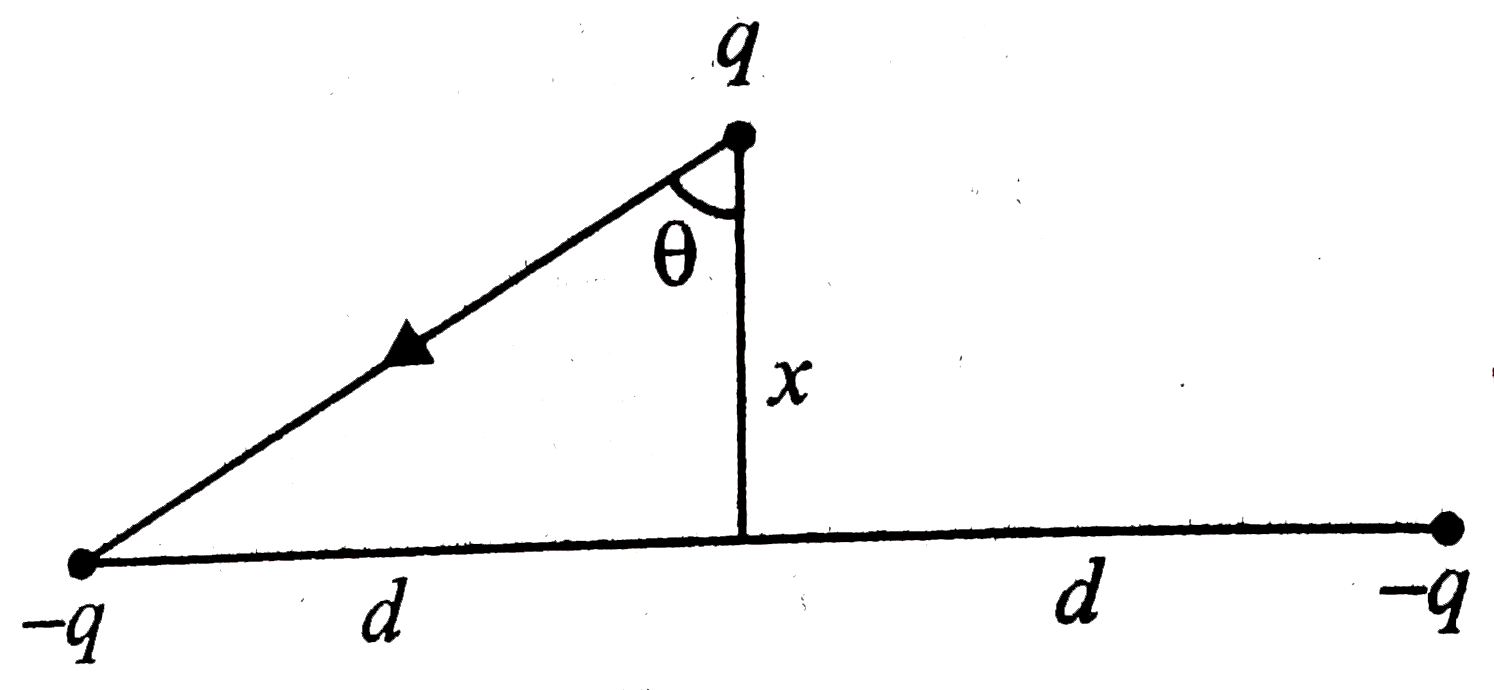
Two charges −q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced at the mid-point is placed slightly by x(x<<d) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillarion of time period.
T=[8π3∈0md3q2]1/2
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
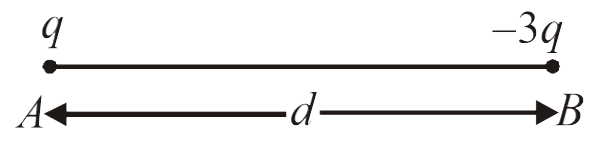
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?

View SolutionTwo charges Q and -3Q are placed fixed on x-axis separated by a distance 'd' Where should a third charge 2Q be placed such that it will not experience any force?
View Solution
