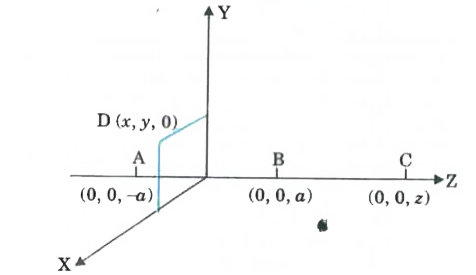
Two charges -q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when $r / a > > 1$ .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?

Video Solution

Text Solution

Verified by Experts

(a) From the figure given below the potential due to the both the charges at point C (0, 0, z) can be calculated as:
$V = \frac{q}{4 π ε_{0} (z - a)} + \frac{(- q)}{4 π ε_{0} (z + a)} = \frac{q (2 a)}{4 π ε_{0} (z^{2} - a^{2})}$
Potential due to both the charges at point D (x, y, 0) will be zero as both the charges are at equal distance from this point.

(b) Potential at any point due to an electric dipole is represented as $V = \frac{1}{4 π ε_{0}} \frac{p cos θ}{r^{2} - a^{2} {cos}^{2} θ}$
(This result has been obtained in the sub-section: 2.3.4(c): Electric potential at a general location due to a short electric dipole)
For short electric dipole $\frac{r}{a} > > 1$
Or, $r > > a$
Thus, $a^{2} {cos}^{2} θ$ can be neglected in comparisonto $r^{2}$ in the denominator. Hence, we can write electric potential due to short electric dipole as:
$V = \frac{1}{4 π ε_{0}} \frac{p cos θ}{r^{2}} \Rightarrow V \propto \frac{1}{r^{2}}$
(c ) As both the charges constituting electric dipole lie on Z-axis and points (5, 0, 0) and (-7, 0, 0) lies on (X-axis), it lies in the equatorial plane of the electric dipole. Thus, potential at both the points are zero and work done in moving a test charge from (5, 0, 0) to (-7, 0, 0) will be zero.
As electrostatic field is conservative in nature, thus the work done by it will be independent of path. Thus answer will remain same, even if the path of the test charge is changed.

Updated on:21/07/2023