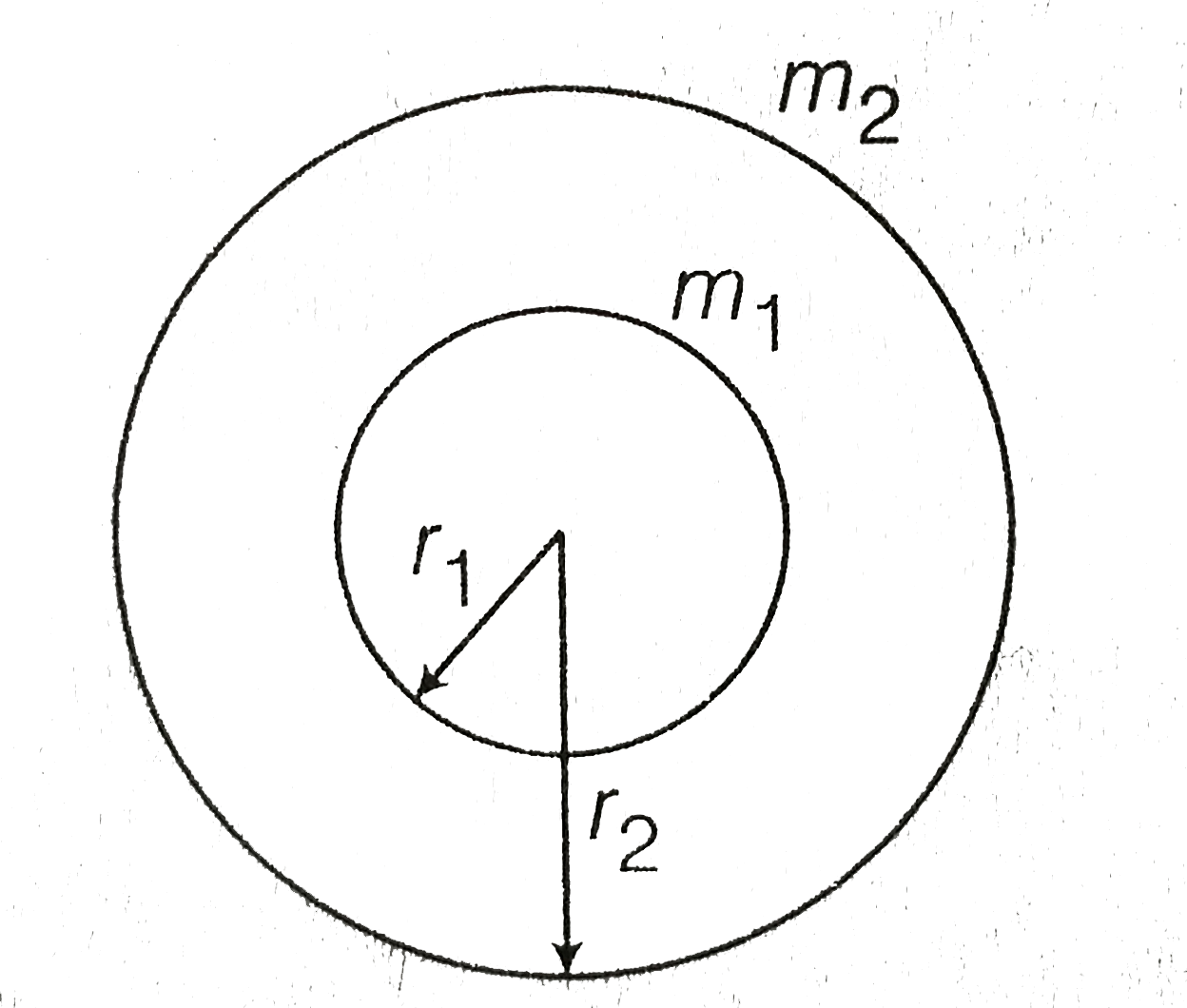
Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?

F=G(M1+M2)r2, for r<r1
F=G(M1+M2)(r2), for r<r2
F=GM2r2, for r1<r<r2
F=GM1r2, for r1<r<r2
The correct Answer is:C
Gravitational field inside a shell is zero, but for points outside it, the shell behaves as if whole of its mass is concentrated at its centre. Hence, for a point lying in between the shells there will be a field only due to the inner shell (=GM2/r2) because the point will be an external point for the inner shell but internal for the outer shell.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field at a distance r ?
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionTwo concentric spherical shells have masses m1andm2 and radii r1andr2(r2>r1). What is the force exerted by this system on a particle of mass m3. If it is placed at a distance r(r1<r<r2) from the centre ?
View SolutionFigure shows two concentric conducting shells of radii r1 and r2 carrying uniformly distributed charges q1 and q2, respectively. Find an expression for the potential of each shell.
 .
.
View SolutionTwo cars of masses m1 andm2 are moving in circles od radii r1andr2. Their speeds are such that they complete one revolution in the same time. The ratio of their angular speed is :
View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
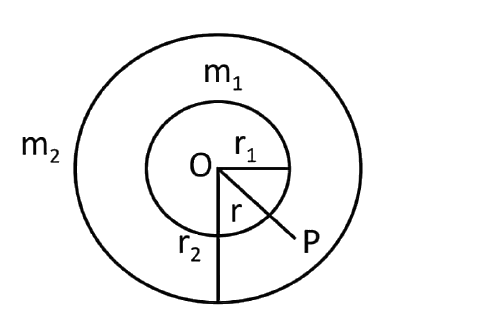
View SolutionTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View Solution

