Two cylinder A and B of radii r and 2r are soldered co-axially. The free end of A is clamped and the free end of B is twisted by an angle ϕ. Find twist at the junction taking the material of tow cylinders to be same and of equal length.
To solve the problem of finding the twist at the junction of two coaxially soldered cylinders A and B, we can follow these steps:
Step 1: Understand the Setup
We have two cylinders:
- Cylinder A with radius r
- Cylinder B with radius 2r
Both cylinders are of equal length L and made of the same material. The free end of cylinder A is clamped, and the free end of cylinder B is twisted by an angle ϕ.
Step 2: Use the Formula for Torque
The torque T for a cylindrical object under torsion is given by:
T=πr42LGθ
where:
- G is the shear modulus of the material,
- θ is the angle of twist,
- r is the radius of the cylinder,
- L is the length of the cylinder.
Step 3: Write the Torque for Each Cylinder
For cylinder A (radius r):
TA=πr42LG(ϕ′−0)=πr42LGϕ′
For cylinder B (radius 2r):
TB=π(2r)42LG(ϕ−ϕ′)=π⋅16r42LG(ϕ−ϕ′)
Step 4: Set the Torques Equal
Since the cylinders are soldered together, the torque transmitted through both must be equal:
TA=TB
Substituting the expressions we derived:
πr42LGϕ′=π⋅16r42LG(ϕ−ϕ′)
Step 5: Simplify the Equation
We can cancel out common terms from both sides:
r4ϕ′=16r4(ϕ−ϕ′)
Dividing by r4 (assuming r≠0):
ϕ′=16(ϕ−ϕ′)
Step 6: Solve for ϕ′
Rearranging gives:
ϕ′+16ϕ′=16ϕ
17ϕ′=16ϕ
ϕ′=1617ϕ
Conclusion
The twist at the junction ϕ′ is:
ϕ′=1617ϕ
We have two cylinders:
- Cylinder A with radius r
- Cylinder B with radius 2r
The torque T for a cylindrical object under torsion is given by:
T=πr42LGθ
where:
- G is the shear modulus of the material,
- θ is the angle of twist,
- r is the radius of the cylinder,
- L is the length of the cylinder.
For cylinder A (radius r):
TA=πr42LG(ϕ′−0)=πr42LGϕ′
TB=π(2r)42LG(ϕ−ϕ′)=π⋅16r42LG(ϕ−ϕ′)
Since the cylinders are soldered together, the torque transmitted through both must be equal:
TA=TB
Substituting the expressions we derived:
πr42LGϕ′=π⋅16r42LG(ϕ−ϕ′)
We can cancel out common terms from both sides:
r4ϕ′=16r4(ϕ−ϕ′)
Dividing by r4 (assuming r≠0):
ϕ′=16(ϕ−ϕ′)
Rearranging gives:
ϕ′+16ϕ′=16ϕ
17ϕ′=16ϕ
ϕ′=1617ϕ
The twist at the junction ϕ′ is:
ϕ′=1617ϕ
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions
21 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions
73 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Solved Examples
159 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Two metallic cylinder made of same material and radii r and 2r are joined as shown in figure. If top end is ved and lower end of cylinder B is twisted by angle e, then angle of twist for cylinder A is (both cylinder have fixed and

View SolutionTwo rod A and B of the same material and dame length have radii r1andr2 respectively. When they are rigidly fixed at one end and twisted by the same couple applied at the other end, find the ratio of the angles of twist at the ends of A and B.
View Solution
Knowledge Check
If two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
Athe same as that of BBtwice that of BCfour times that of BDone-fourth that of BA long wire hangs vertically with its upper end clamped, when a torque of 2 Nm is applied to the free end, it is twisted through an angle of 30∘. Then the potential energy of the twisted wire is
Aπ joulesBπ/3 joulesCπ/6 joulesDπ/4 joulesTwo wires A and B of same material and same mass have radius 2r and r. If resistance of wire A is 34Ω, then resistance of B will be
A544ΩB372ΩC68ΩD17Ω
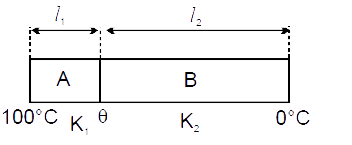
Two rods A and B of different materials but same cross section are joined as in figure. The free end of A is maintained at 100°C and the free end of B is maintained at 0°C. If l2=2l1,K1=2K2 and rods are thermally insulated from sides to prevent heat loses then the temperature θ of the junction of the two rods is
View SolutionTwo cylinders A and B of the same matieral have same length, their radii being in the ratio of 1:2 repectively. They are joined end to end as shown in figure. The upper end of A is rigidly fixed. The lower end of B is twised through an angle θ, the angle of twist of the cylinder A is:

View SolutionFind the elastic deformation energy of a steel rod whose one end is fixed and the other is twisted through an angle φ=6.0∘. The length of the rod is equal to l=1.0m, and the radius to r=10mm.
View SolutionTwo rods A and B of the same material and length have radii r1 and r2respective. When they are rigidly fixed at one end and twisted by the same torque applied at the other end, the ratio [the angle of twist at the end of Athe angle of twist at the end of B] equal to
View SolutionA rod of length l and radius r is joined to a rod of length l/2 and radius r/2 of same material. The free end of small rod is fixed to a rigid base and the free end of larger rod is given a twist of θ∘, the twist angle at the joint will be
View Solution
