Two discs A and B are mounted co-axially one vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The rotation x1/x2 is.
2
12
√2
1√2
The correct Answer is:C
12I(2ω)2=12kx21 and 12I(ω)2=12kx22
dividing then we get
x1x2=√2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Two discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period isView SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
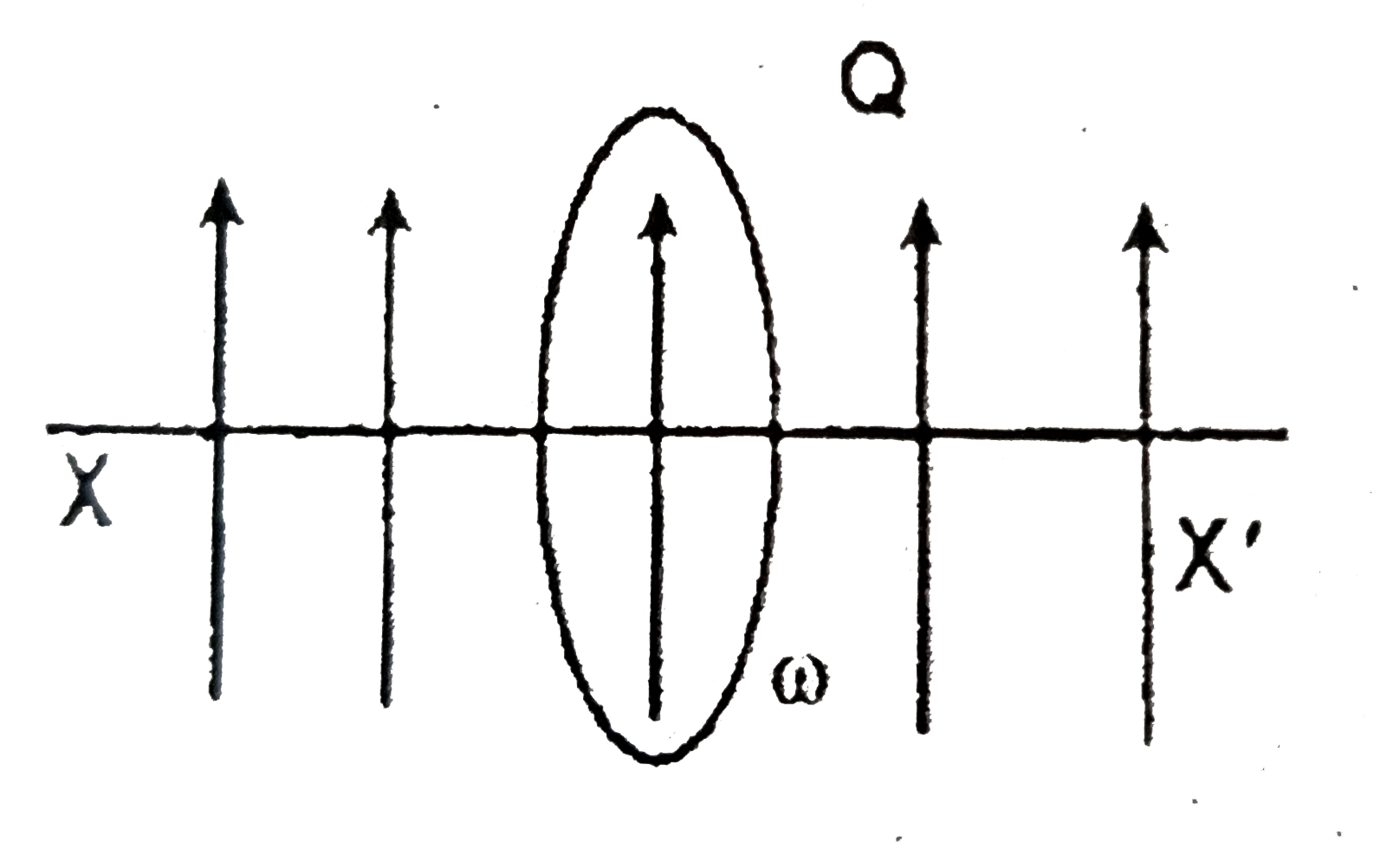View Solution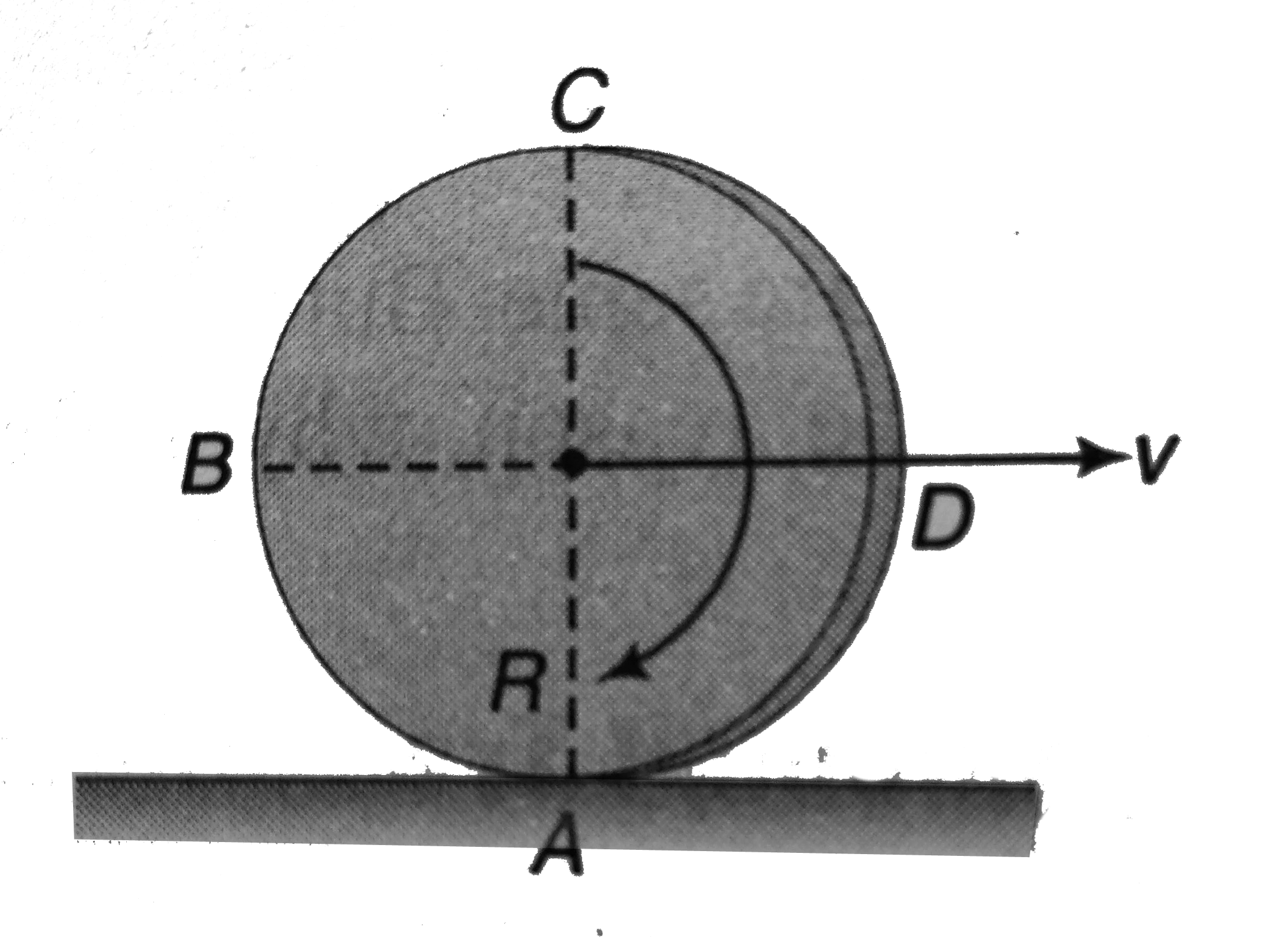
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.View SolutionTwo discs are mounted on frictionless bearings on a common shaft. The first disc has rotational inertia / and is spinning with angular velocity ω. The second disc has rotational inertia 2/ and is spinning in opposite direction with angular velocity 3ω, as shown in figure. The two discs are slowly forced towards each other along the shaft until they couple and have a final common angular velocity of
View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution