A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
Linear momentum
Angular momentum
kinetic energy
Moment of inertia
The correct Answer is:b
To solve the problem, we need to analyze the situation when a child sits on a rotating disc. The key concepts involved are angular momentum, moment of inertia, and the effects of external forces.
1. Identify the System:
We have a disc rotating about its center with an initial angular velocity ω. When a child sits on the disc, we need to determine what physical quantity remains conserved.
2. Understand the Forces Acting:
When the child sits on the disc, the gravitational force mg acts downward on the child. This force is directed towards the center of the disc, which means it does not create any torque about the axis of rotation.
3. Determine External Torque:
Since the gravitational force acts parallel to the axis of rotation, it does not exert any torque on the system. Therefore, the net external torque acting on the system is zero.
4. Apply the Conservation of Angular Momentum:
According to the principle of conservation of angular momentum, if no external torque acts on a system, the angular momentum of that system remains constant. Therefore, the angular momentum before the child sits on the disc will equal the angular momentum after the child sits down.
5. Analyze Moment of Inertia:
When the child sits on the disc, the moment of inertia of the system increases because the child adds mass to the disc. The moment of inertia I is given by I=Idisc+mchildr2, where r is the distance from the axis of rotation to where the child is sitting.
6. Relate Angular Momentum and Angular Velocity:
The angular momentum L of the system is given by L=Iω. Since I increases when the child sits down, and L is conserved, the angular velocity ω must decrease to keep L constant.
7. Conclusion:
The quantity that remains conserved when the child sits on the disc is the angular momentum. Therefore, the answer to the question is that angular momentum is conserved.
Final Answer:
Angular momentum is conserved.
---
We have a disc rotating about its center with an initial angular velocity ω. When a child sits on the disc, we need to determine what physical quantity remains conserved.
When the child sits on the disc, the gravitational force mg acts downward on the child. This force is directed towards the center of the disc, which means it does not create any torque about the axis of rotation.
Since the gravitational force acts parallel to the axis of rotation, it does not exert any torque on the system. Therefore, the net external torque acting on the system is zero.
According to the principle of conservation of angular momentum, if no external torque acts on a system, the angular momentum of that system remains constant. Therefore, the angular momentum before the child sits on the disc will equal the angular momentum after the child sits down.
When the child sits on the disc, the moment of inertia of the system increases because the child adds mass to the disc. The moment of inertia I is given by I=Idisc+mchildr2, where r is the distance from the axis of rotation to where the child is sitting.
The angular momentum L of the system is given by L=Iω. Since I increases when the child sits down, and L is conserved, the angular velocity ω must decrease to keep L constant.
The quantity that remains conserved when the child sits on the disc is the angular momentum. Therefore, the answer to the question is that angular momentum is conserved.
Angular momentum is conserved.
Similar Questions
Knowledge Check
A disc is rotating with angular velocity ω. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by
A(→r×→F).→ωB(→r×→F)×→ωC→r.(→F×→ω)D→r×(→F.→ω)
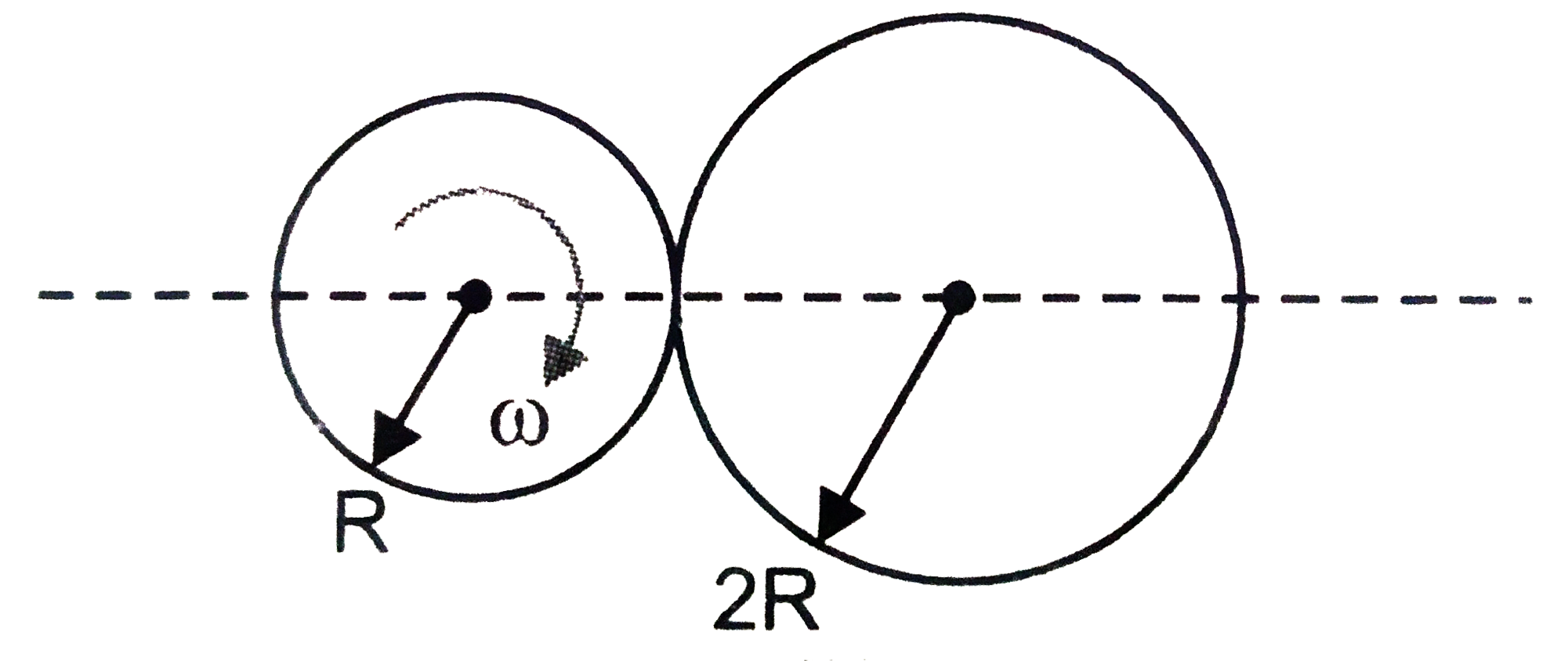
Two discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionA disc is rotaing with an angular velocity ω0. A constant retarding torque is applied on it to stop the disc. The angular velocity becomes ω02 after n rotations. How many more rotations will it make before coming to rest ?
View SolutionA disc is rolling without slipping with angular velocity ω. P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is

View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View SolutionTwo identical discs are positioned on a vertical axis as shown in the figure. The bottom disc is rotating at angular velocity ω0 and has rotational kinetic energy K0.The top disc is initially at rest. It then falls and sticks to the bottom disc. The change in the rotational kinetic energy of the system is

View Solution

