Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
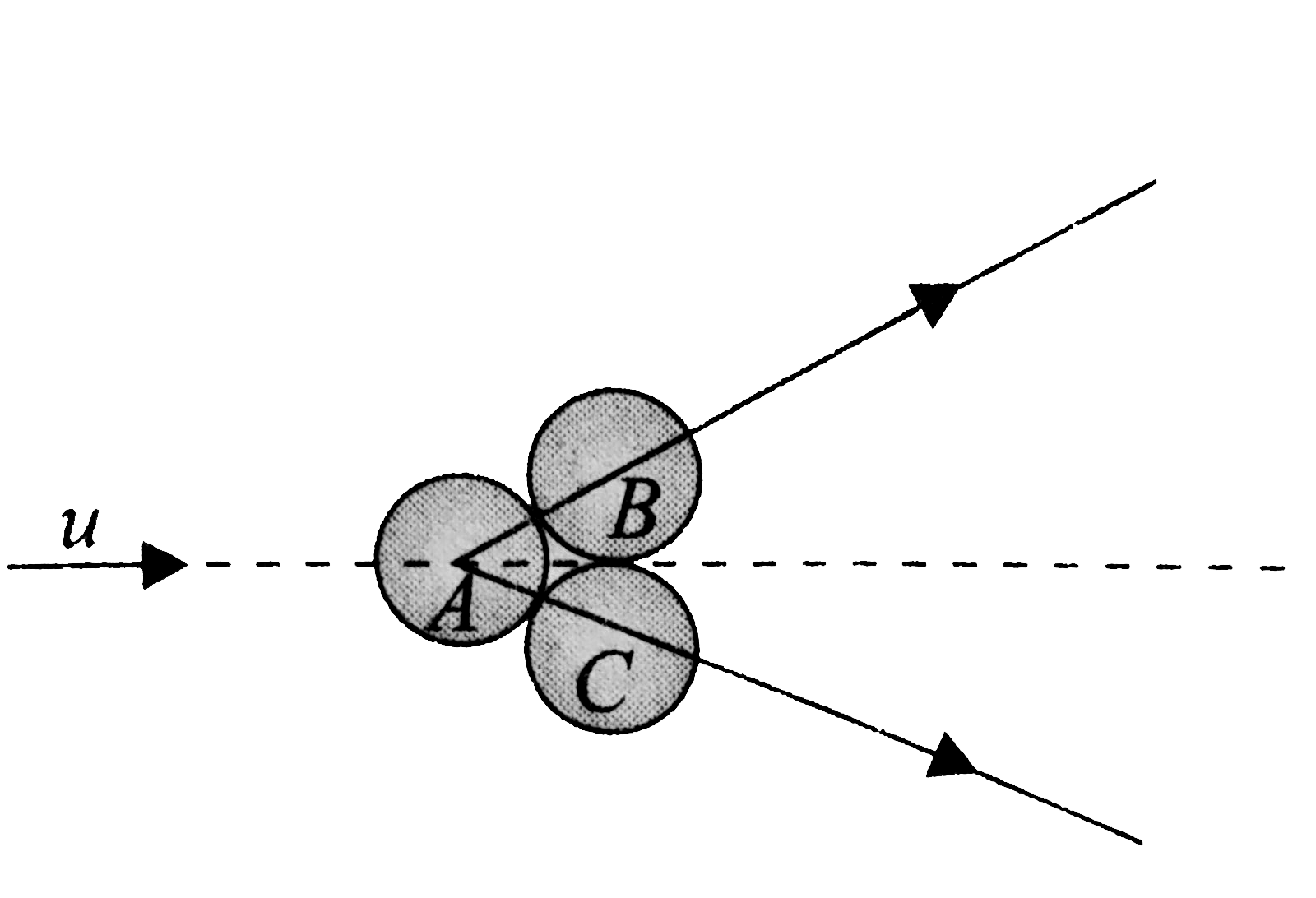
Find the velocity acquired by each of the spheres B and C after collision.
u√3
2u√3
u2√3
u2
The correct Answer is:C
u=velocity of sphere A before impact. As the spheres are identical, the triangle ABC formed by joining their centres is equilateral. The spheres B and C will move in direction AB and AC after impact making can angle of 30∘ with the origina lines of motion of ball A.
Let v be the speed ofthe balls B and C after impact.
Momentum conservation gives
(m2)u=mvcos30∘+mvcos30∘
u=2√3v⇒v=u2√3.......i
From Newton's experimental law, for an oblique collision, we have take components along normal, i.e. along AB for balls A and B.
vB−vA=−e(uB−uA)
v−0=−e(0−ucos30∘)
v=eucos30∘.........ii
Combining eqn i and ii we get e=13
Loss in KE=12m2u2−2(12mv2)
=14μ2−m(u2√3)2=16μ2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
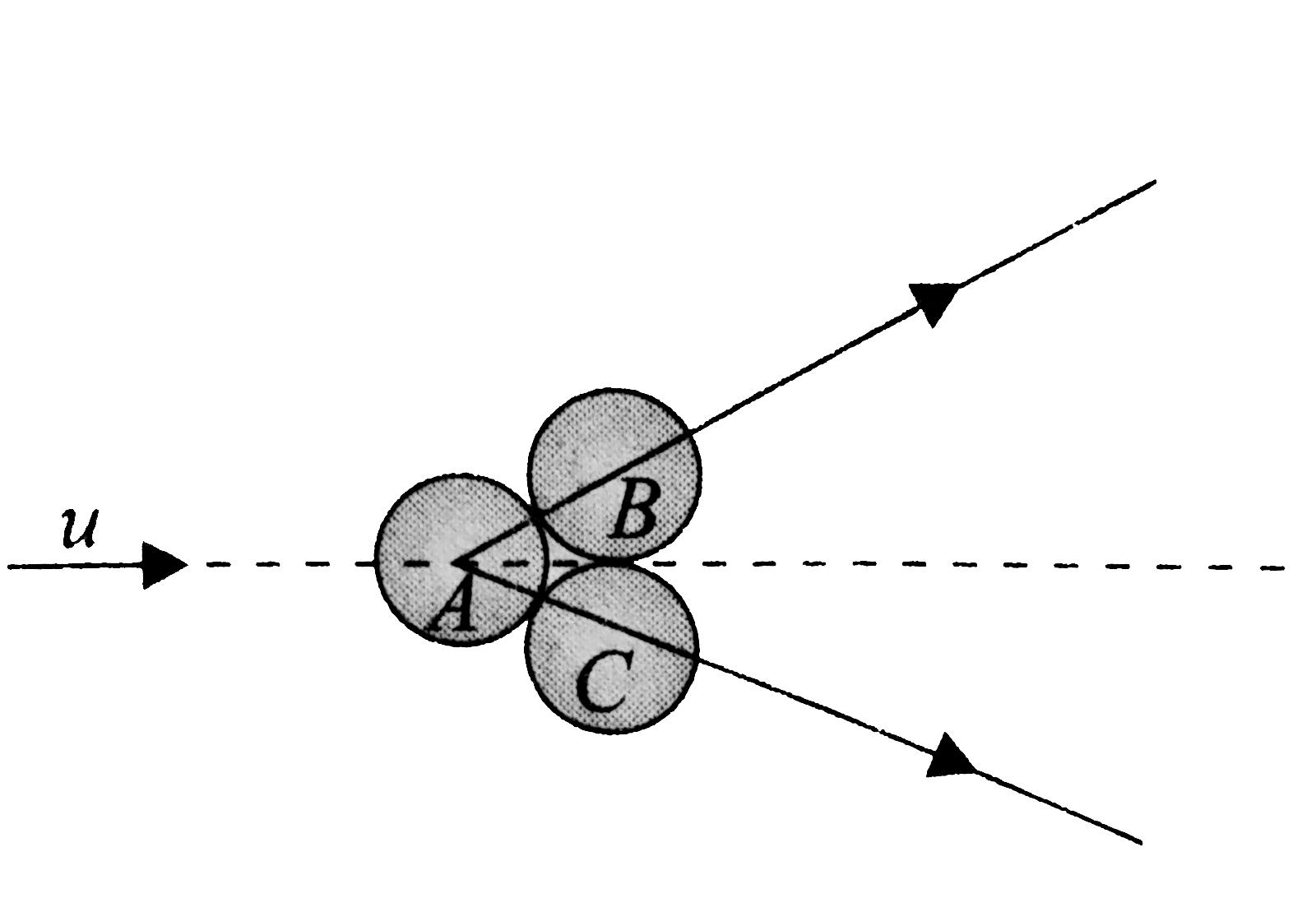
The loss of KE during collision is
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
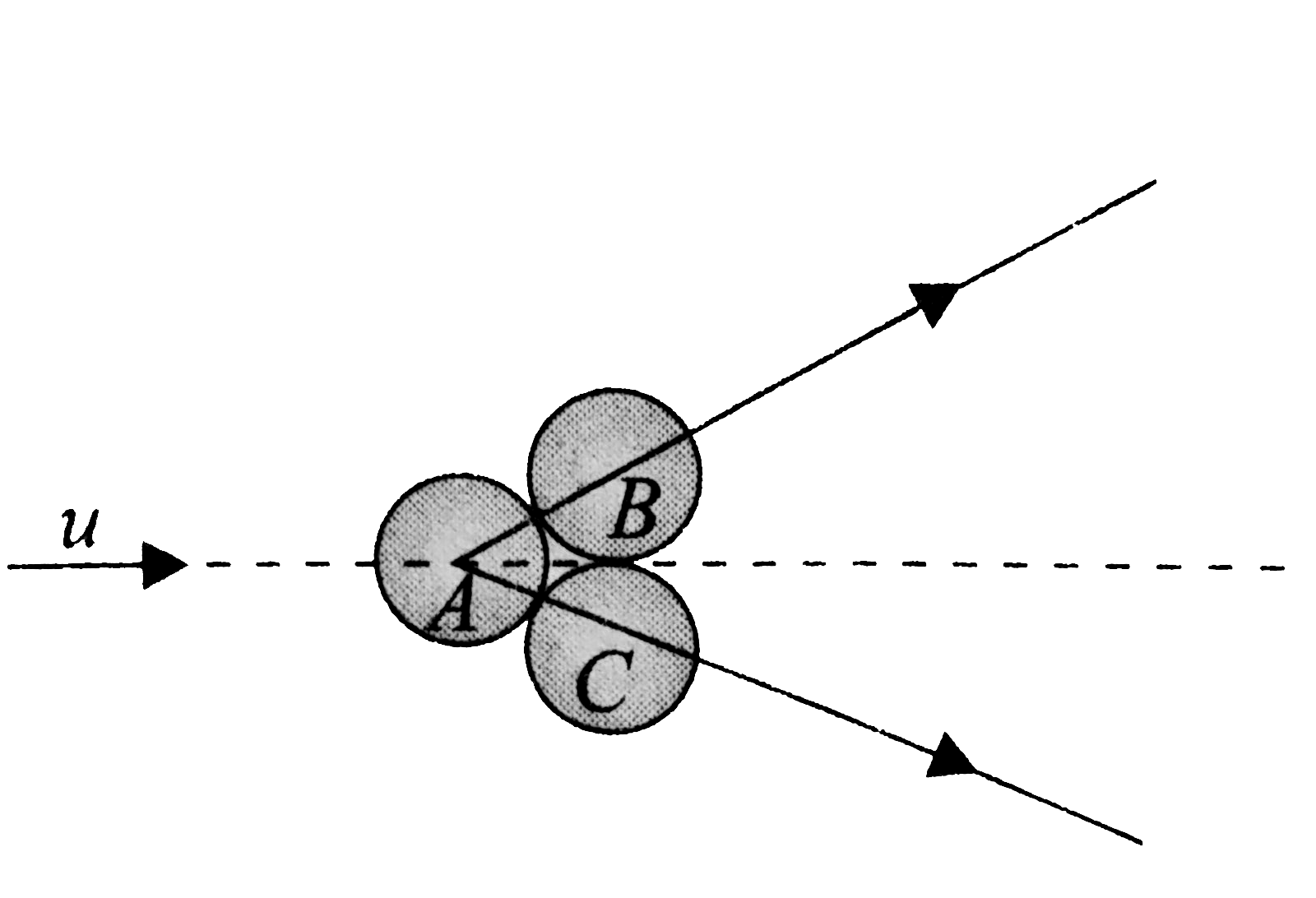
The coefficient of restitution between the two spheres A and B (or between A and C) is
View Solution
Knowledge Check
Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.

The loss of KE during collision isAmu28Bmu26Cmu23Dmu22Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.

The coefficient of restitution between the two spheres A and B (or between A and C) isA1/3B1/4C2/3D3/4Two equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on them and reduces to rest. Then:
 ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2
ACoefficient of restitution is e=23BLoss of kinetic energy 16mu2 where u is velocity before impactCAfter the collision, velocity of equal mass sphere is u√3DLoss of kinetic energy 13mu2
Two equal sphere of mass m are in contact o a smooth horizontal table. A third identical sphere impinges symmetrically on them and is reduced to rest. Find e and the loss KE.

View SolutionTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on the and is reduced to rest. Prove that e=23 and find the loss in KE.
View SolutionTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on the and is reduced to rest. Prove that e=23 and find the loss in KE.
View SolutionA smooth hollow U shaped tube of mass 2m is lying at rest on a smooth horizontal table. Two small balls of mass m, moving with velocity u enter the tube simultaneously in symmetrical fashion. Assume all collisions to be elastic. Find the final velocity of the balls and the tube.
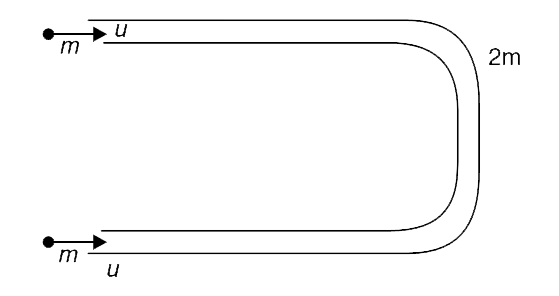
View SolutionA sphere of mass m moving with a velocity u hits another stationary sphere of same mass. If e is the coefficient of restitution, what is the ratio of the velocities of two spheres after the collision?
View Solution
