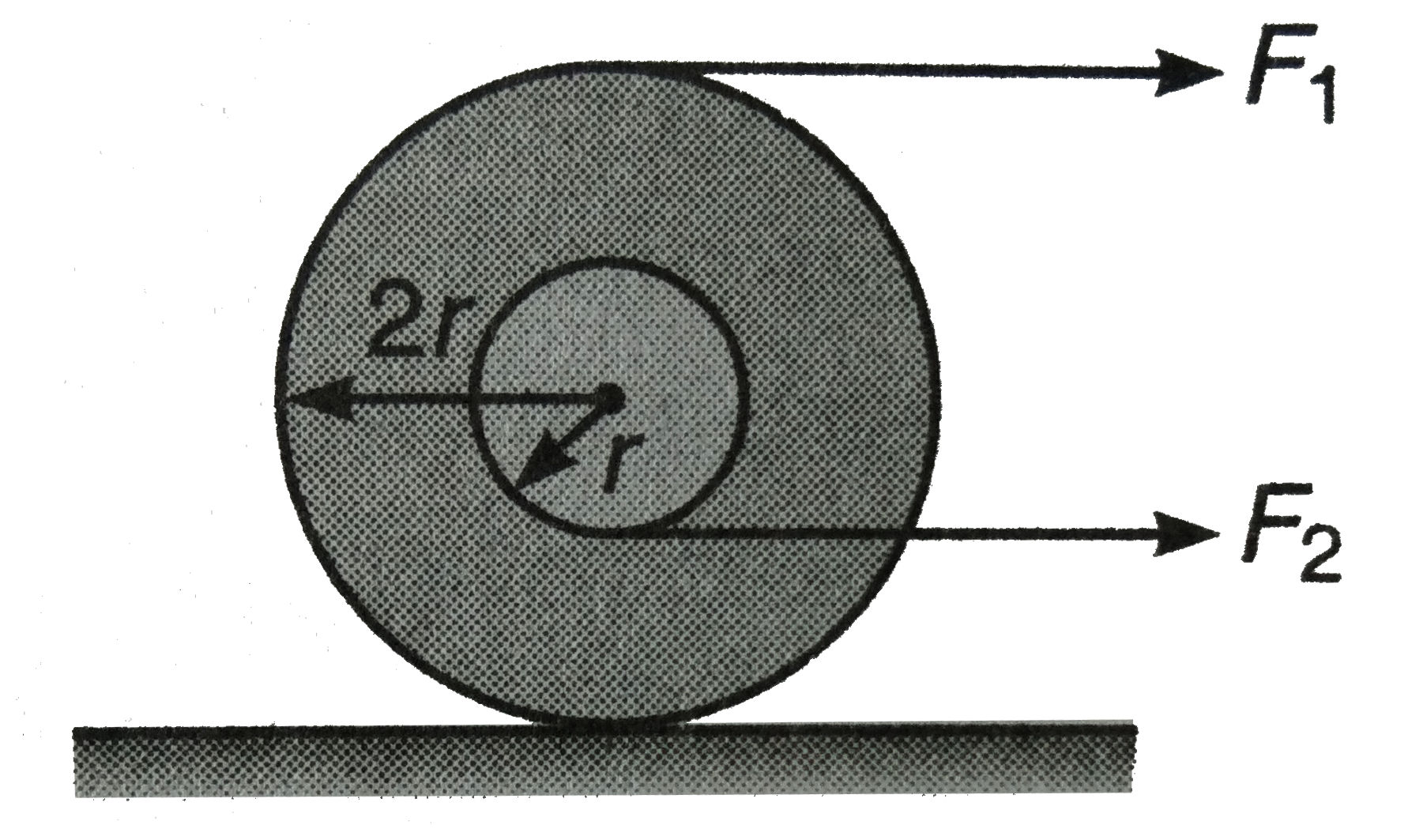
Two forces F1 and F2 are applied on a spool of mass M and moment of inertia I about an axis passing through its centre of mass. Find the ratio F1F2. So that the force of friction is zero. Given that I<2Mr2.
a=Rα by applied forces
∴F1+F2M=2r[F1(2r)−F2(r)I] ltbr> Solving these two equations we get
F1F2=I+2Mr24Mr2−I
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Two masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionFind the moment of inertia of a hemisphere of mass M shown in figure - 5.28 , about an axis AA' passing through its centre of mass .
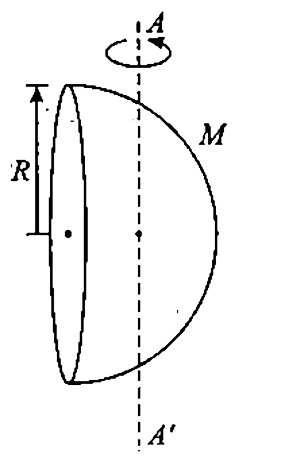
[[83320MR2]]
View Solution
Knowledge Check
Assertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
I=Icm+Mr2AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.Two partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg−m2)
A6B9C8D12A light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
Am1m2m1+m2l2Bm1+m2m1m2l2C(m1+m2)l2D√m1m2l2
Calculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
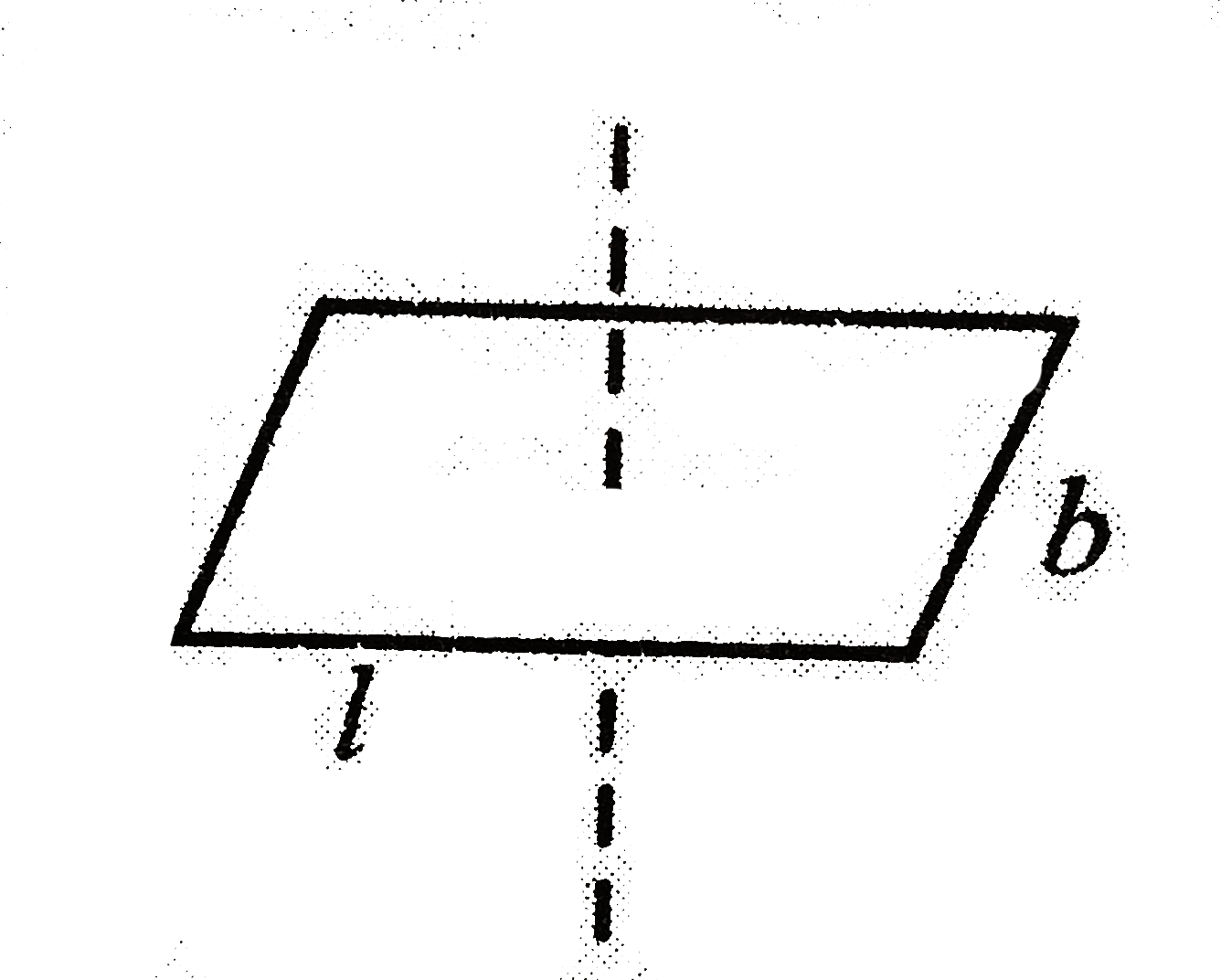
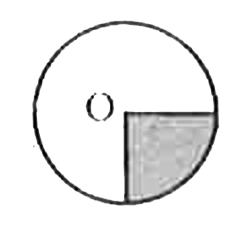
View SolutionThe M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
View SolutionThe moment of inertia of a sphere of mass M and radius R about an axis passing through its centre is 25MR2 . The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is
View Solution
