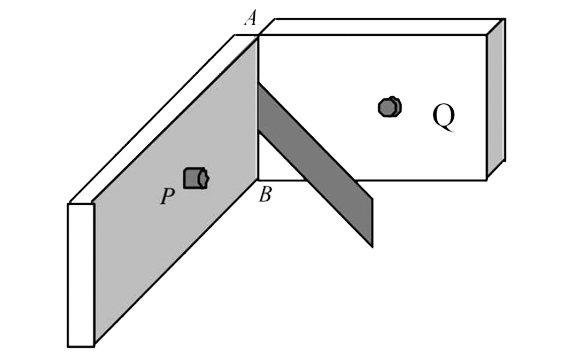
Two heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacle is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
The correct Answer is:A, B, C, D
Ic=1.2kg−m2
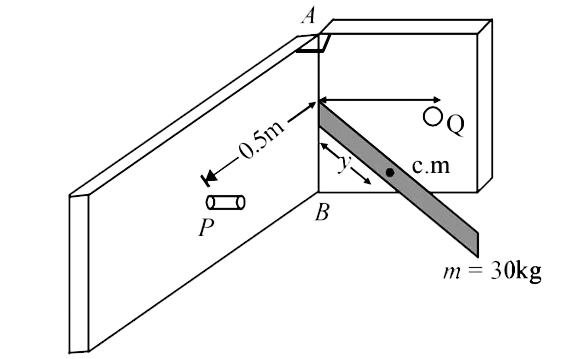
Let y be the distance of c.m. from line AB.
Applying parallel axis theorem of M.I. we get
M.I. of lamiar sheet about AB
IAB=Ic.m.+my2
IAB=12+30y2…..(i)
The angular velocity of the laminar sheet will change after
impulse = Change in linear momentum
6=30(vf−Vi)
6=30×y(ωf−ωi)..(ii)
Also, change in angular momentum = Moment of impulse
∴IABωf−IABωi=imps–e×distance
IAB(ωf−ωi)=6×0.5=3
∴ωf=3IAB+ωi=31.2+30y2+(−1)...(iii)
Note: Minus sign with ωi because the direction of laminar
plate towards the obstacle is taaken as - ve (assumption).
From (ii) and (iii)<br>6 = 30 xxy [(3)/(1.2+30y^2)-1+1]<br>1 = 5y[(3)/(1.2 + 30y^2]<br>:. 1.2 +30y^2 = 5y[+3] = 15y<br>:. 30yk^2 - 15y - 1.2 = 0<br>Onsolv∈gwe≥ty=0.1or0.4<br>:. omega_f = 1red/s if we puty y = 0.1 in eq. (ii)<br>Andoemga_f = 0.5 rad/s if we put y = 0.4 in eq. (ii)
(Not valid as per sign convention)
Now, since the lamina sheet comes back with same angular
speed as that of incident angular speed, the sheet will sming
in between P and Q infinitely.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Calculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View Solution
Knowledge Check
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2A light rod of length l has two masses m1 and m2 attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
Am1m2m1+m2l2Bm1+m2m1m2l2C(m1+m2)l2D√m1m2l2A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A(m1+m2)l2B√m1m2l2Cm1m2m1+m2l2Dm1+m2m1m2l2
Consider a uniform square plate of side 'a' and mass 'm'. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is
View SolutionConsider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View SolutionConsider a uniform square plate of side 'a' and mass 'm' The moment of inertia of heis plate about an axis perpendiucalar to its plane and passing through one of its corners is
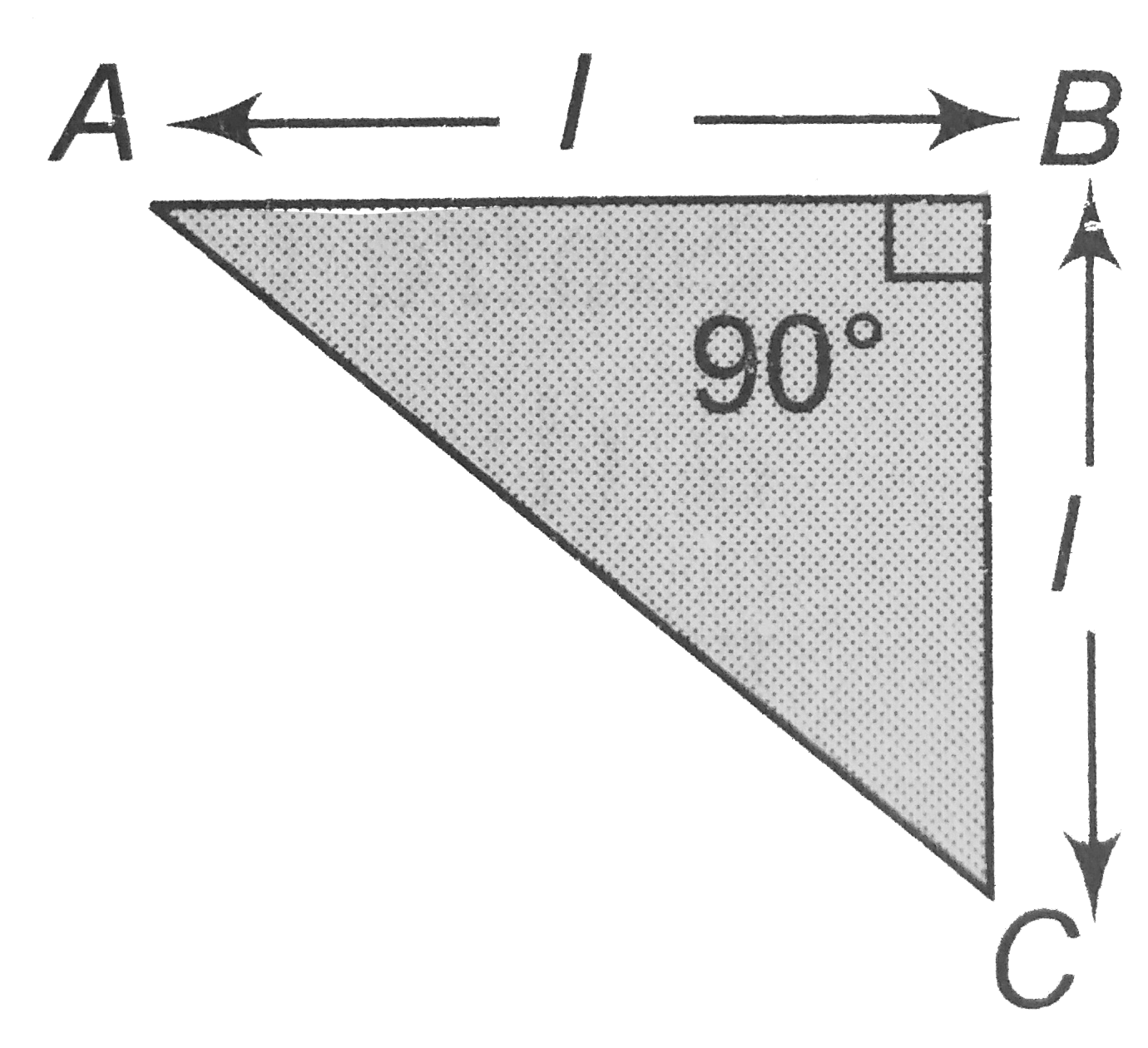
View SolutionFigure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
 .
.
View SolutionIf I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
View Solution
