Calculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.

Video Solution

Text Solution

Verified by Experts

For the rod of mass M and length $l$ the moment of inertia of the rod about an axis AB passing through its centre of mass is given, $I_{A B} = \frac{M I^{2}}{12}$

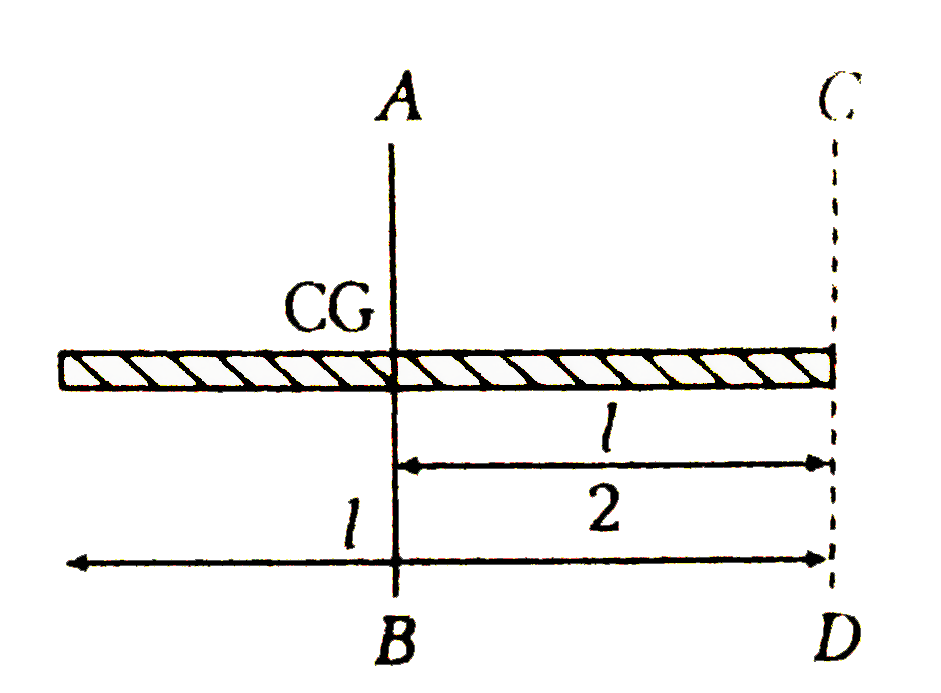
According to the parallel axes theorem,
$I_{C D} = I_{A B} + M {(\frac{1}{2})}^{2} = \frac{M l^{2}}{12} + \frac{M l^{2}}{4}$
$= \frac{M l^{2} + 2 M l^{2}}{12} = \frac{4 M l^{2}}{12} = \frac{M l^{2}}{3}$
$I_{C D} = \frac{M l^{2}}{3} = \frac{2 {(5)}^{2}}{3} = \frac{50}{3} {kg-m}^{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a rod of mass 'M', length ? about an axis perpendicular to it through one end is,
A $\frac{M l^{2}}{2}$ ,
B $\frac{M l^{2}}{3}$
C $\frac{M l^{2}}{12}$
DNone of these
Question 2 - Select One
Moment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
A $M L^{\frac{2}{4}}$
B $M L^{\frac{2}{6}}$
C $M L^{\frac{2}{12}}$
D $M L^{\frac{2}{2}}$
Question 3 - Select One
The moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
A $\frac{M L^{2}}{6}$
B $\frac{M L^{2}}{12}$
C $\frac{7 M L^{2}}{24}$
D $\frac{7 M L^{2}}{48}$

DC PANDEY-ROTATION-(C) Chapter Exercises

Home
Ask Doubt
Profile