Two holes are made at a depth of h and 5 h from the water surface in a water container kept on a horizontal surface as shownn in figure. For which value of r, equalt amount of water will come out of the two holes? Here, l is the length of side of the square hole and r is the radius of circular hole.
To solve the problem of finding the radius r for which equal amounts of water will come out of two holes at different depths in a container, we can follow these steps:
1. Identify the Variables:
- Let the depth of the first hole (A) be h.
- Let the depth of the second hole (B) be 5h.
- The first hole is circular with radius r.
- The second hole is square with side length L.
2. Use Torricelli's Law:
- According to Torricelli's theorem, the velocity of efflux v of a fluid under gravity through a hole is given by:
v=√2gh
- For hole A (at depth h):
v1=√2gh
- For hole B (at depth 5h):
v2=√2g(5h)=√10gh
3. Calculate the Cross-Sectional Areas:
- The area of hole A (circular):
A1=πr2
- The area of hole B (square):
A2=L2
4. Apply the Equation of Continuity:
- The volume flow rate (discharge) through both holes must be equal:
QA=QB
- Therefore:
A1v1=A2v2
- Substituting the areas and velocities:
πr2√2gh=L2√10gh
5. Simplify the Equation:
- Cancel √gh from both sides:
πr2√2=L2√10
- Rearranging gives:
r2=L2√10π√2
6. Solve for r:
- Taking the square root:
r=√L2√10π√2=L√√10π√2
- This can be simplified further:
r=L⋅√10√2π=L⋅√5π1/2
7. Final Result:
- Thus, the value of r for which equal amounts of water will come out of the two holes is:
r=L√5√π
- Let the depth of the first hole (A) be h.
- Let the depth of the second hole (B) be 5h.
- The first hole is circular with radius r.
- The second hole is square with side length L.
- According to Torricelli's theorem, the velocity of efflux v of a fluid under gravity through a hole is given by:
v=√2gh
- For hole A (at depth h):
v1=√2gh
- For hole B (at depth 5h):
v2=√2g(5h)=√10gh
- The area of hole A (circular):
A1=πr2
- The area of hole B (square):
A2=L2
- The volume flow rate (discharge) through both holes must be equal:
QA=QB
- Therefore:
A1v1=A2v2
- Substituting the areas and velocities:
πr2√2gh=L2√10gh
- Cancel √gh from both sides:
πr2√2=L2√10
- Rearranging gives:
r2=L2√10π√2
- Taking the square root:
r=√L2√10π√2=L√√10π√2
- This can be simplified further:
r=L⋅√10√2π=L⋅√5π1/2
- Thus, the value of r for which equal amounts of water will come out of the two holes is:
r=L√5√π
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
A squre hole of side length l is made at a depth of h and a circular hole is made at a depht of 4 h from the surface of water in a water tank kept on a horizontal surface (where l ltlt h). Find the radius r of the circular hole if equal amount of water comes out of the vessel through the holes per second.
View SolutionIn a vessel of water a hole is made at a depth of 3.5 m from the free surface. What would be the velocity of efflux ?
View Solution
Knowledge Check
- Question 1 - Select One or More
Two holes 1 and 2 are made at depths h and 16h reapectively. Both the holes are circular but radius of hole-1 is two times.
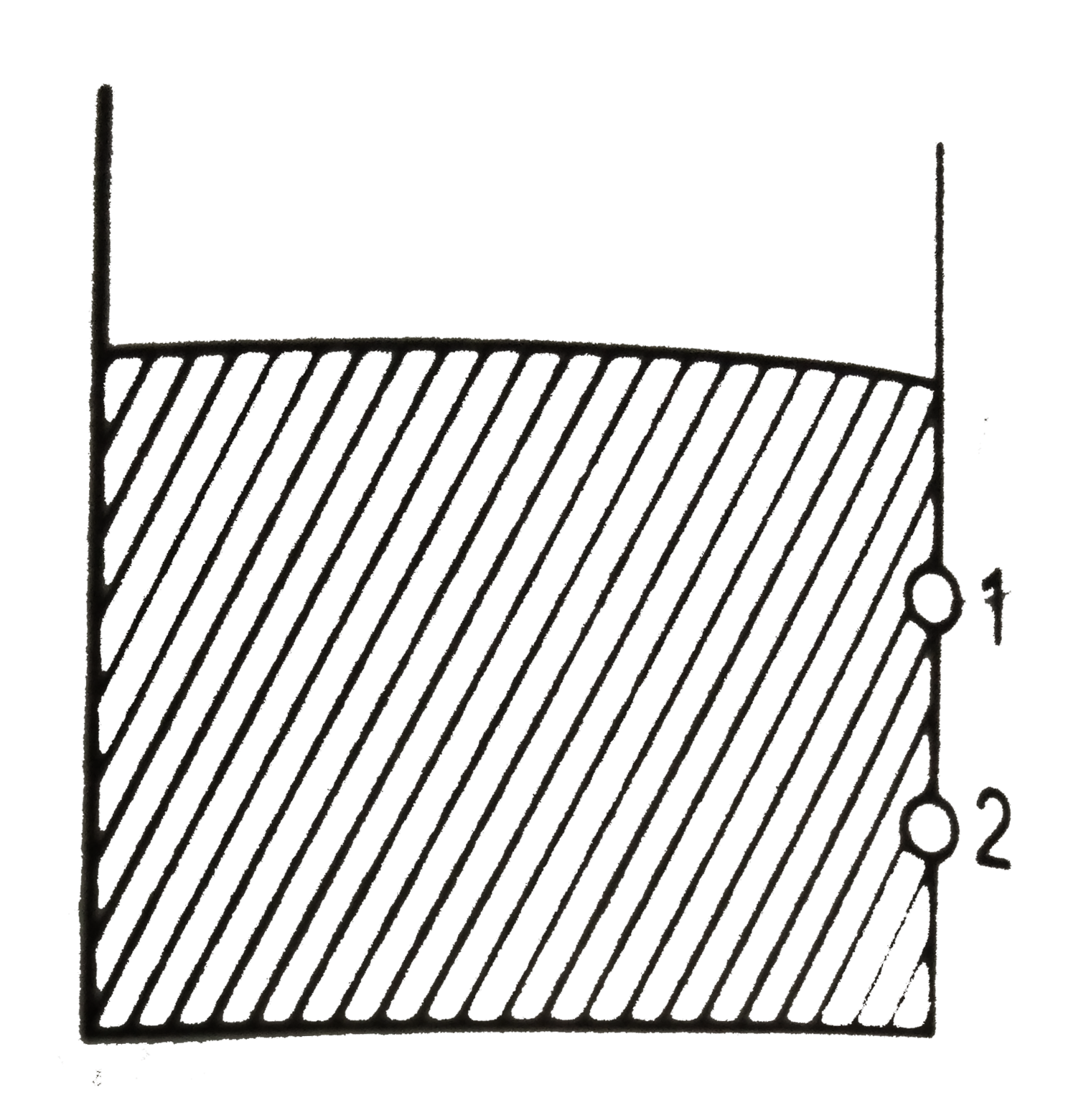 AInitially equal volumes of liquid will flow from both the holes in unit timeBIntially more volume of liquid will flow from hole-2 per unit time.CAfer some time more volume of liquid will flow from hole-1 per unit time.DAfter some time more volume of liquid will flow from hole-2 per unit time
AInitially equal volumes of liquid will flow from both the holes in unit timeBIntially more volume of liquid will flow from hole-2 per unit time.CAfer some time more volume of liquid will flow from hole-1 per unit time.DAfter some time more volume of liquid will flow from hole-2 per unit time - Question 2 - Select One
A tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
A2H√3B√3H2C√3HD3H4 - Question 3 - Select One
Two holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3cm above the bottom, then the distance of the other holes from the top surface of water is
A32cmB√6cmC√3cmD3cm
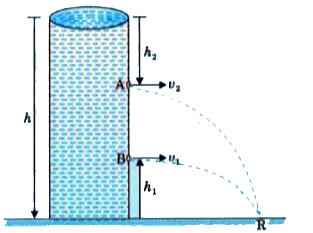
On the wall of a cylindrical water tank, two holes are made as shown in figure. Water coming out from these holes hits the ground at the same point. What will be the ration h1h2?
 View Solution
View SolutionIn a cylindrical water tank there are two small holes Q and P on the wall at a depth of h1 from the upper level of water and at a height of h2 from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of h1 and h2 is
 View Solution
View SolutionThere are two holes P and Q at depths h and 4h from the top of a large vessel, completely filled with water. P is a square hole of side L and Q is a circular hole of radius r. If the same quantity of water flows out per second from both the holes, then the relation between L and r is
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA tube is attached as shown in closed vessel containing water. The velocity of water coming out from a small hole is :
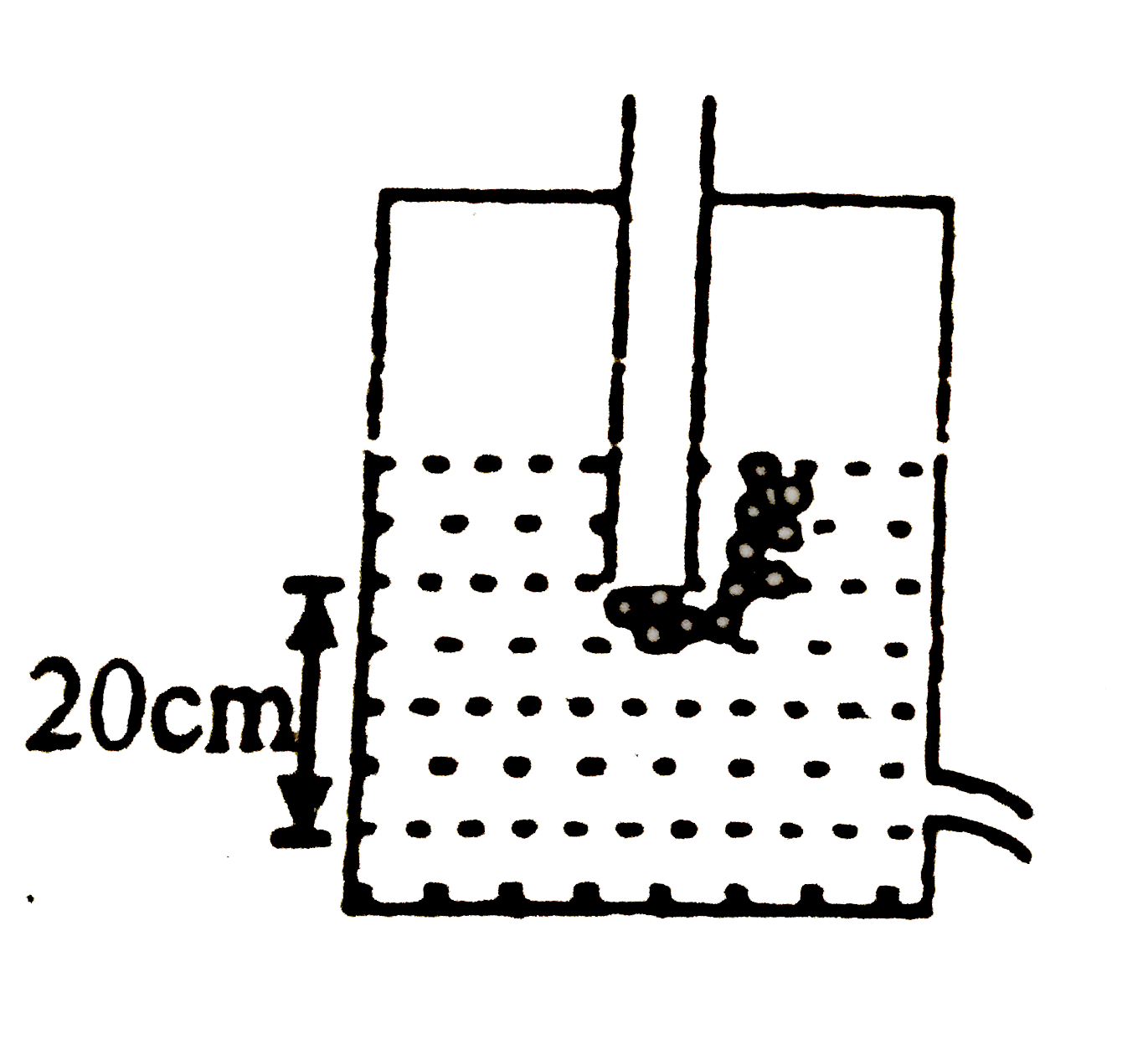 View Solution
View Solution

