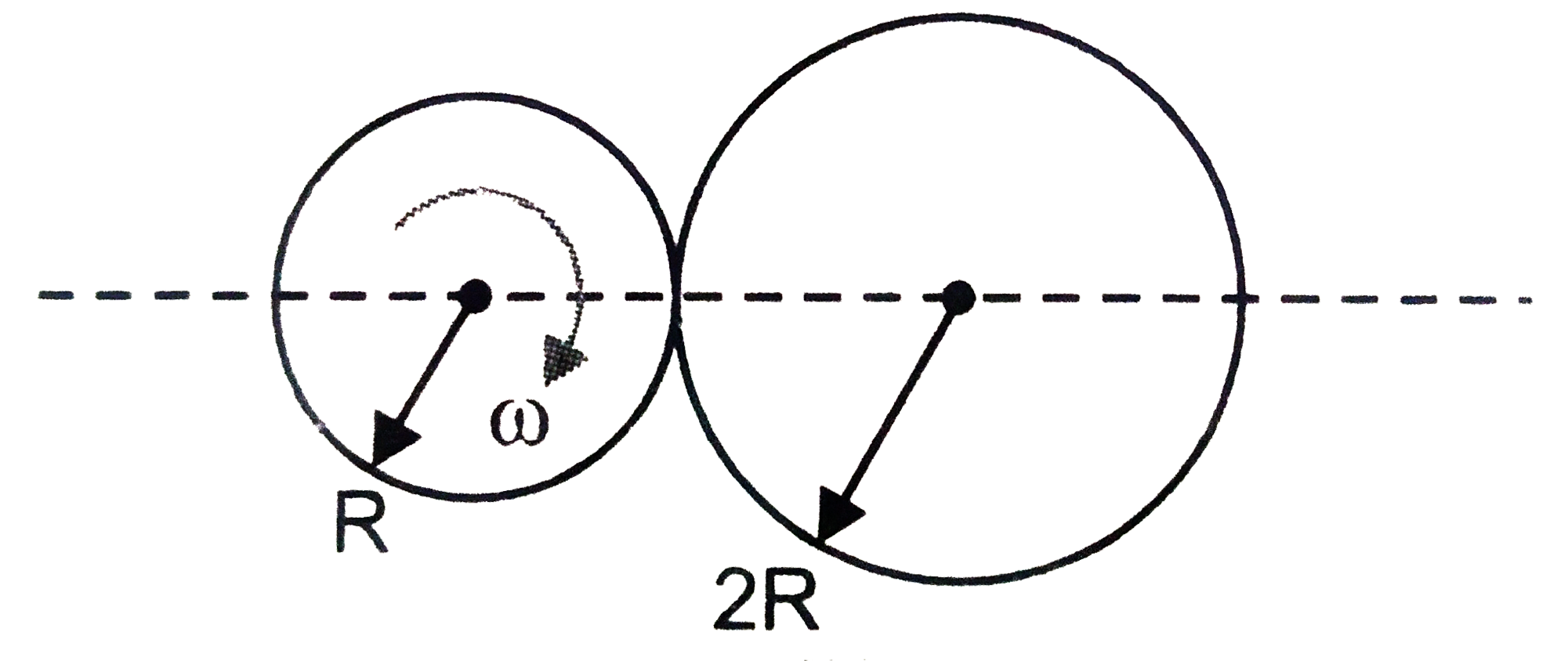
Two horizontal discs of different radii are free to rotate about their central vertical axes: One is given some angular velocity, the other is stationary. Their rims arc now brought in contact. There is friction between the rims. Then
the force of friction between the rims will disappear when the discs rotate with equal angular speeds
the force of friction between the rims will when they have equal linear velocities
the angular momentum of the system will conserved
the rotational kinetic energy of the system will not conserved
The correct Answer is:B, D
To solve the problem, we need to analyze the situation involving two discs with different radii, one of which is rotating while the other is stationary. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have two discs:
- Disc A: Rotating with an angular velocity ω1.
- Disc B: Stationary, with an angular velocity ω2=0.
When the rims of the two discs come into contact, friction will act at the point of contact.
Hint: Visualize the discs and their rotation directions. Consider the effects of friction when they touch.
Step 2: Analyze the Effect of Friction
When the two discs touch, friction will act to oppose the relative motion between them. Since Disc A is rotating and Disc B is stationary, there will be a tendency for Disc B to start rotating in the same direction as Disc A due to the frictional force.
Hint: Remember that friction acts to prevent relative motion between surfaces.
Step 3: Condition for No Relative Motion
The friction force will disappear when both discs rotate with the same angular velocity. This means that if the angular velocities of both discs become equal (ω1=ω2), there will be no relative motion at the point of contact, and thus no frictional force acting on them.
Hint: Think about when two objects moving at the same speed will not experience friction between them.
Step 4: Conservation of Angular Momentum
In this scenario, angular momentum is not conserved because there is an external torque due to friction acting between the discs. However, the angular momentum of the system can be analyzed before and after contact.
Hint: Consider how external forces (like friction) affect the conservation laws.
Step 5: Kinetic Energy Considerations
While angular momentum may not be conserved due to the frictional forces, the rotational kinetic energy of the system will not be conserved either. Some energy will be lost due to friction as heat.
Hint: Remember that energy can be transformed and lost in non-conservative systems.
Conclusion
Based on the analysis:
1. The friction between the rims will disappear when the discs rotate with equal angular speeds.
2. The rotational kinetic energy of the system will not be conserved due to energy losses from friction.
Final Answer: Both statements regarding the disappearance of friction at equal angular speeds and the non-conservation of rotational kinetic energy are true.
We have two discs:
- Disc A: Rotating with an angular velocity ω1.
- Disc B: Stationary, with an angular velocity ω2=0.
When the two discs touch, friction will act to oppose the relative motion between them. Since Disc A is rotating and Disc B is stationary, there will be a tendency for Disc B to start rotating in the same direction as Disc A due to the frictional force.
The friction force will disappear when both discs rotate with the same angular velocity. This means that if the angular velocities of both discs become equal (ω1=ω2), there will be no relative motion at the point of contact, and thus no frictional force acting on them.
In this scenario, angular momentum is not conserved because there is an external torque due to friction acting between the discs. However, the angular momentum of the system can be analyzed before and after contact.
While angular momentum may not be conserved due to the frictional forces, the rotational kinetic energy of the system will not be conserved either. Some energy will be lost due to friction as heat.
Based on the analysis:
1. The friction between the rims will disappear when the discs rotate with equal angular speeds.
2. The rotational kinetic energy of the system will not be conserved due to energy losses from friction.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Two discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionA uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.
View SolutionTwo men each of mass m stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass M and is free to rotate about a vertical axis passing through its centre of mass. Each mass start simultaneously along the rim clockwise and reaches their original starting positions on the disc. The angle turned through by disc with respect to the ground (in radian) is
View SolutionA stationary horizontal disc is free to rotate about its axis. When a torque is applied on it its, kinetic energy as a function of θ, where θ is the angle by which it has rotated, is given as kθ. If its moment of inertia is I then the angular acceleration of the disc is :
View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View Solution
The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity ω0. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.
View SolutionTwo discs of same moment of inertia rotating their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to the face coinciding the axis of rotation. The expression for loss of enregy during this process is :
View SolutionTwo discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is
View Solution
