Two identical blocks A and B, each of mass m, are connected to each other with a spring of length L [Fig.1.51].
![Two identical blocks A and B, each of mass m, are connected to each other with a spring of length L [Fig.1.51]. Force constant of the spring is k. The system is kept on a horizontal table. An identical third block C moving with a velocity v along the line AB collides with A elastically . (i) What is the kinetic energy of the system A-B in the most compressed state ?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XI_P1_U04_C01_SLV_069_Q01.png)
Force constant of the spring is k. The system is kept on a horizontal table. An identical third block C moving with a velocity v along the line AB collides with A elastically .
(i) What is the kinetic energy of the system A-B in the most compressed state ?
The velocity of block C, just before collision =v. As the collision of C with A is elastic , the block C comes to rest just after collision ,and the block A gets the velocity v in the forward direction . Because of the spring between A and B gradually decrease, but that of B gradually increases, and the spring is compressed. As soon as velocities of the blocks A and B becomes equal , the spring attains maximum compression and the system A-B begins to move with a common velocity v1.
From the law of conservation of momentum,
mv=2m×v1
or,v1=v2
∴ At maximum compression of the spring kinetic energy of the system A-B
=12(2m)v21=12×2m×v24=14mv2
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - SECTION RELATED QUESTIONS
24 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
38 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
Two blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View Solution
Knowledge Check
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2kTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2kA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x-axis with velocity vo collides elastically with block A at time t = 0. Then,
 Adisplacement time equation of A after collision will be x=x0−v0√mksinωtBdisplacement time equation of A after collision will be x=x0+v0√mksinωtCvelocity of B just after collision will be aw towards positive x-direction.Dvelocity of B just after collision will be vo towards positive x-direction.
Adisplacement time equation of A after collision will be x=x0−v0√mksinωtBdisplacement time equation of A after collision will be x=x0+v0√mksinωtCvelocity of B just after collision will be aw towards positive x-direction.Dvelocity of B just after collision will be vo towards positive x-direction.
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
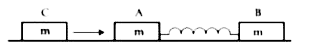
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x -axis with velocity v0 collides elastically with block A at time t=0. Then
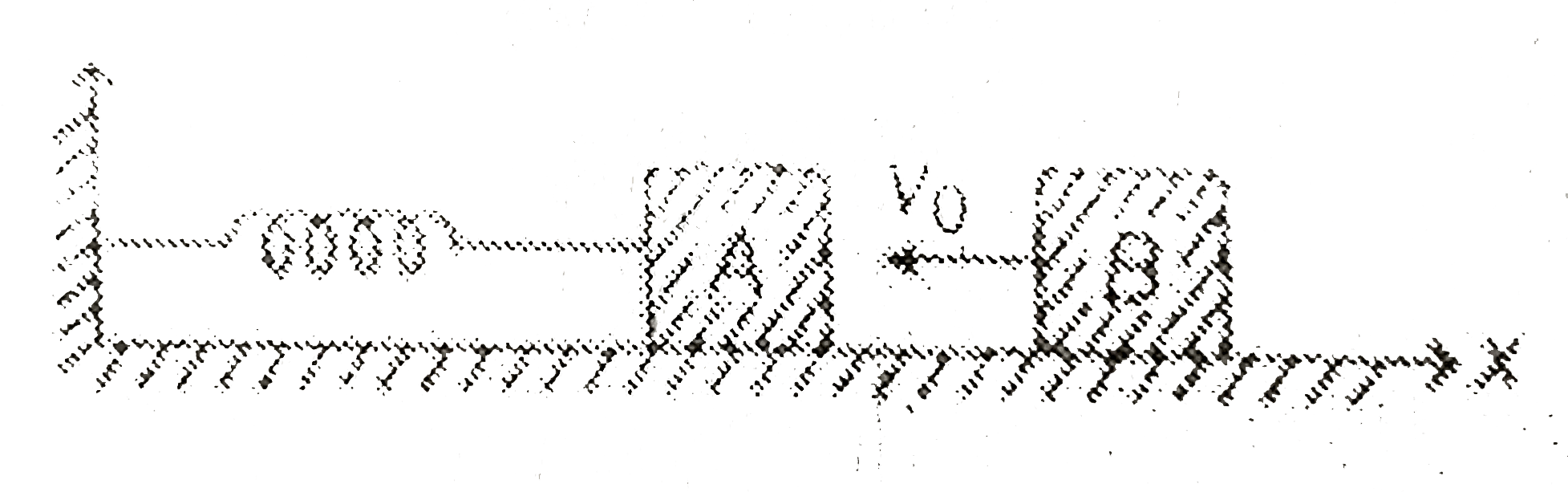
View Solution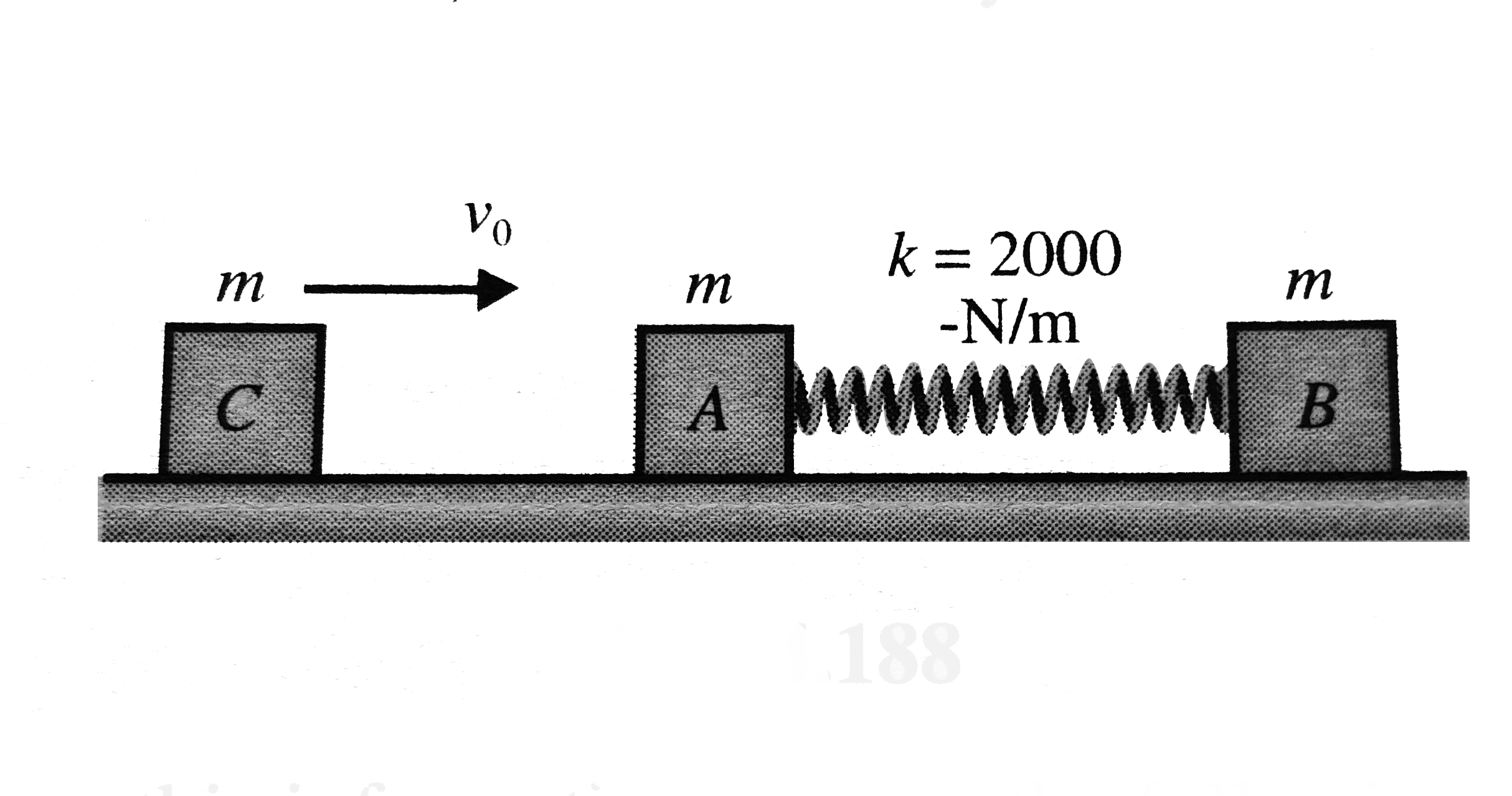
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. Oscillation energy of the system i.e., part of the energy which is oscillation (changing) between potention and kinetic forms is
View Solution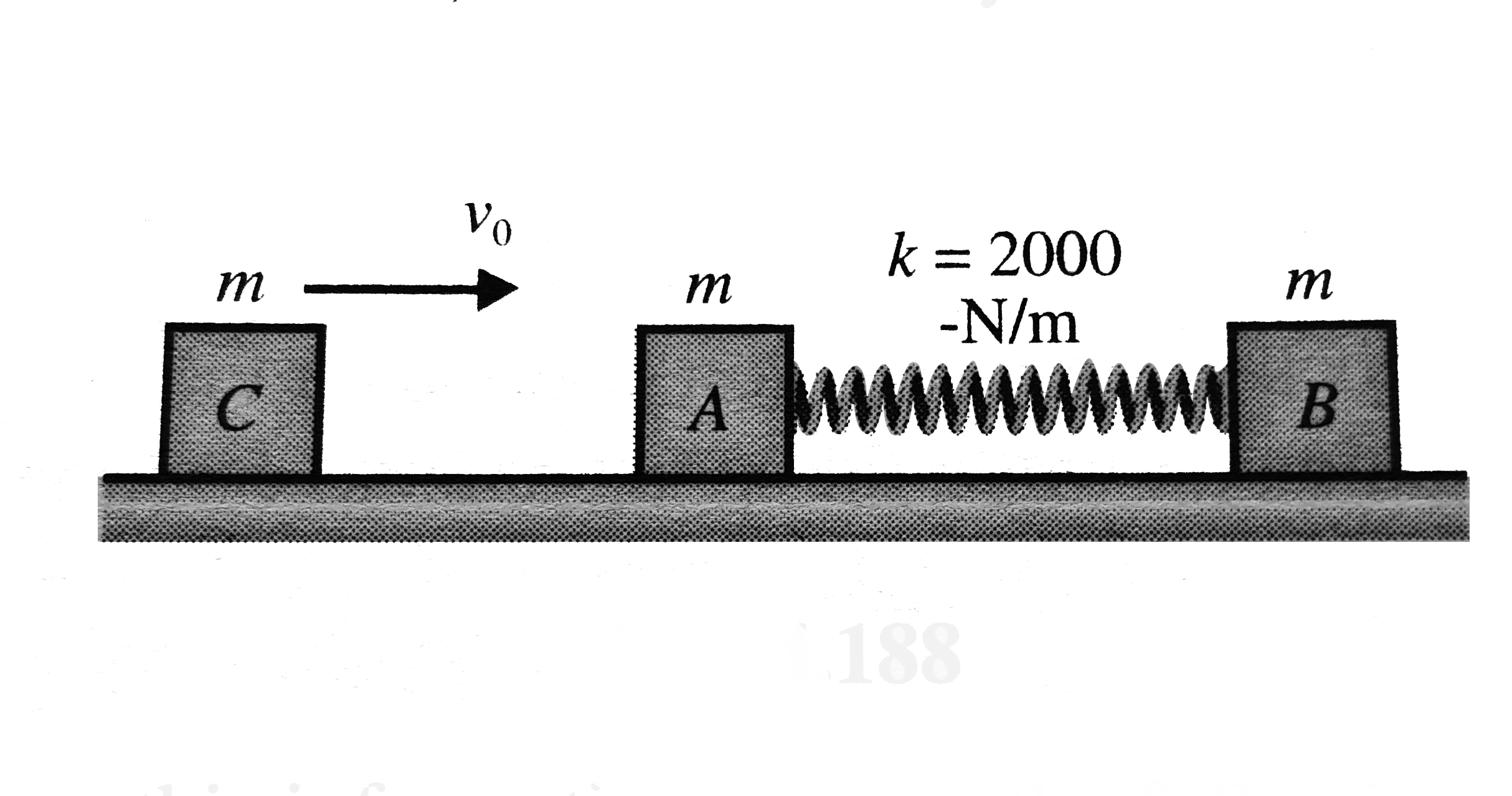
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. Oscillation energy of the system i.e. part of the energy which is oscillating between potential and kinetic forms
View Solution
