Two identical blocks A and B, each of mass m, are connected to each other with a spring of length L [Fig.1.51].
![Two identical blocks A and B, each of mass m, are connected to each other with a spring of length L [Fig.1.51]. Force constant of the spring is k. The system is kept on a horizontal table. An identical third block C moving with a velocity v along the line AB collides with A elastically . (ii) What is the maximum compression of the spring ?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CHY_DMB_PHY_XI_P1_U04_C01_SLV_069_Q01.png)
Force constant of the spring is k. The system is kept on a horizontal table. An identical third block C moving with a velocity v along the line AB collides with A elastically .
(ii) What is the maximum compression of the spring ?
If the maximum compression of the spring is x, then potential energy of the compressed spring
=12kx2=12mv2−14mv2=14mv2
or,x2=m2kv2
or,x=v=√m2k.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - SECTION RELATED QUESTIONS
24 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
38 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
Two blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View Solution
Knowledge Check
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2kTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2kThe ball sticks to block C, then block Ccollides elastically , head - on with A. If the maximum compression is x0, the spring constant k is
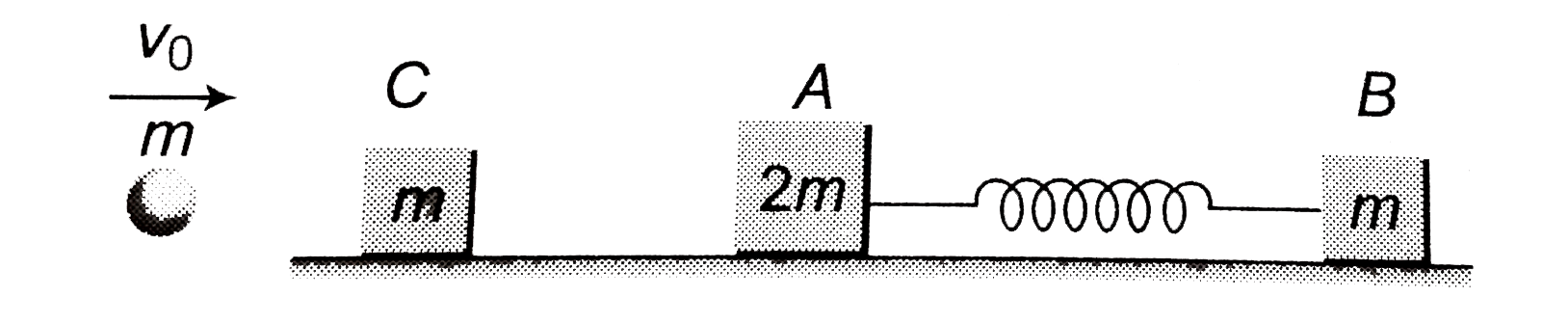 A23mv20x20Bmv202x20Cmv203x20Dmv206x20
A23mv20x20Bmv202x20Cmv203x20Dmv206x20
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
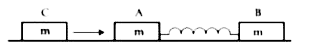
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
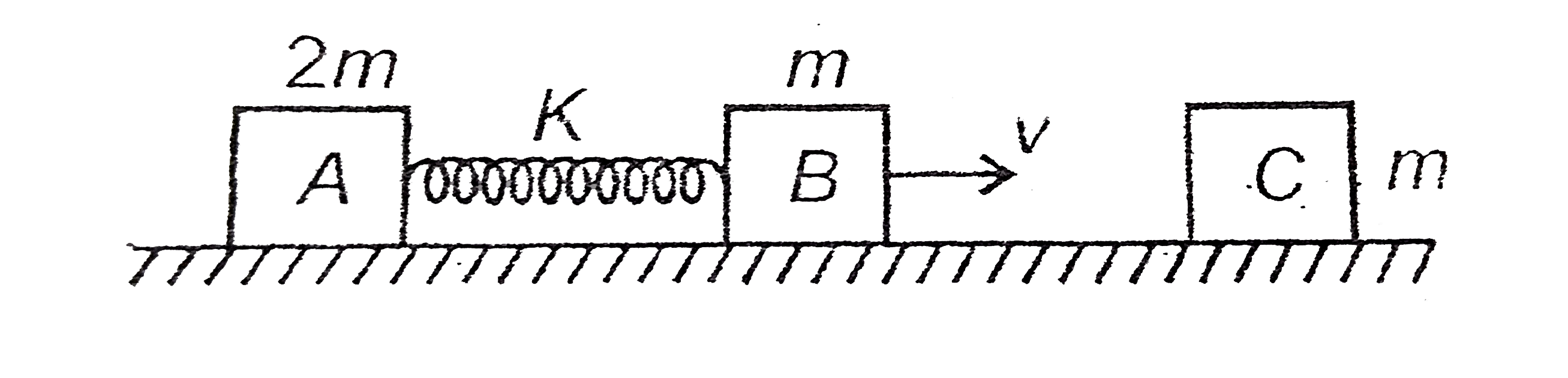
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be

View SolutionTwo identical blocks, each of mass m, are connected through a massless spring of force constant k and arranged as shown in fig the spring is compressed by an amount y by applying an external force and released
(a) What is the velocity of upper block when the spring is relaxed
(b) What should be the initial compression of the spring so that the lower block is just raised above the floor ?

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View Solution
