Two identical conducting rings A and B of radius R are rolling over a horizontal conducting plane with same speed v but in opposite direction. A constant magnetic field B is present pointing into the plane of paper. Then the potential difference between the highest points of the two rings is
(a) 0
(b) 2BvR
(c ) 4BvR
(d) none of these
The correct Answer is:C
( c) V2−V1=12Bω(2R)2=2BR(ωR)=2BRv
V3−V4=2BRv
But V1=V3
→ V2−V4=4BRv
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct23videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning8videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective13videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK40videos
ELECTROMAGENTIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
Similar Questions
Two conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
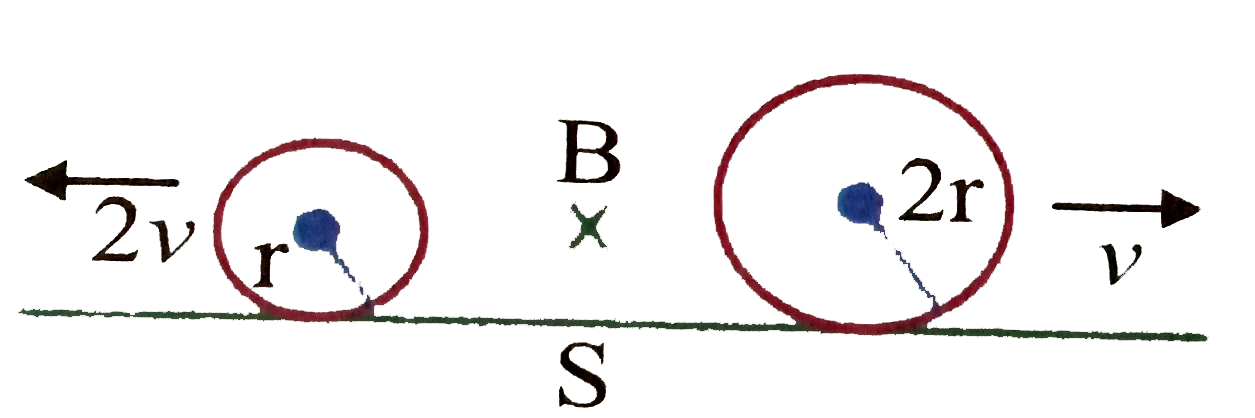
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
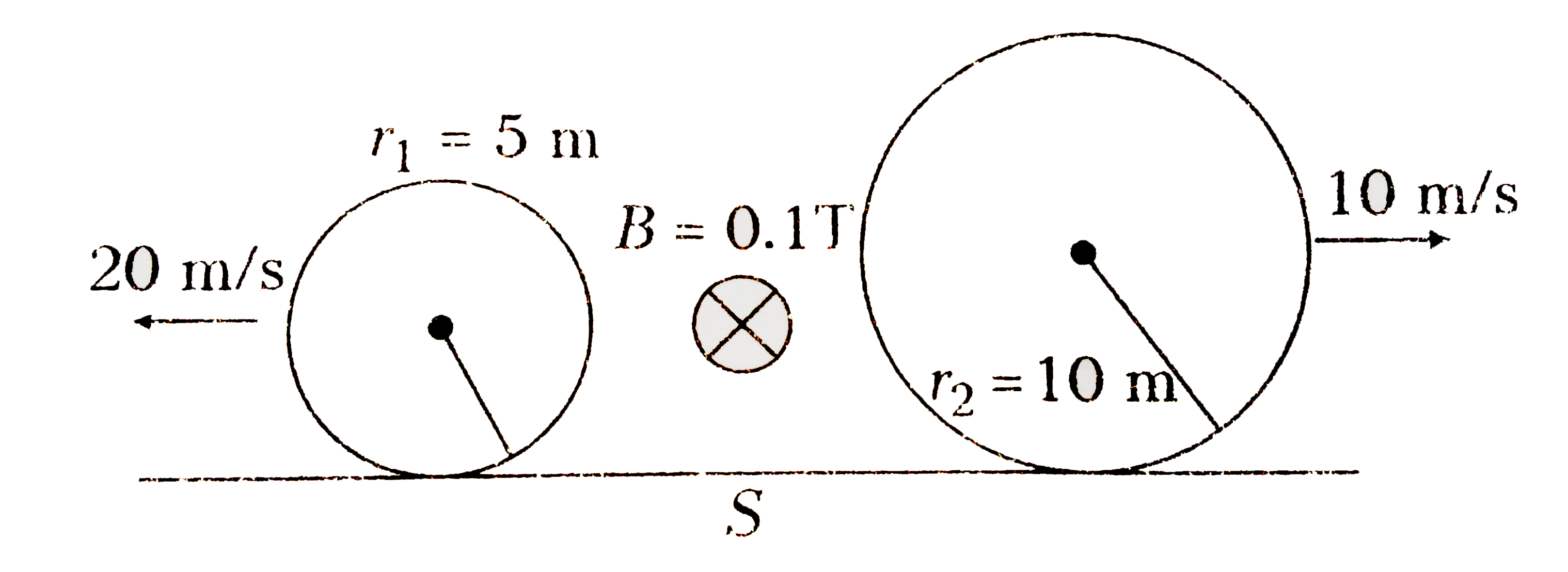
View Solution
Knowledge Check
- Question 1 - Select One
Two identical conducing ring A and B of radius R are in pure rolling over a horizontal conducing plane with same speed (of center of mass) v but in opposite direction. A constant magnetic field B is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is:
AZeroB2BvRC4BvRDNone of these - Question 2 - Select One
Two conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
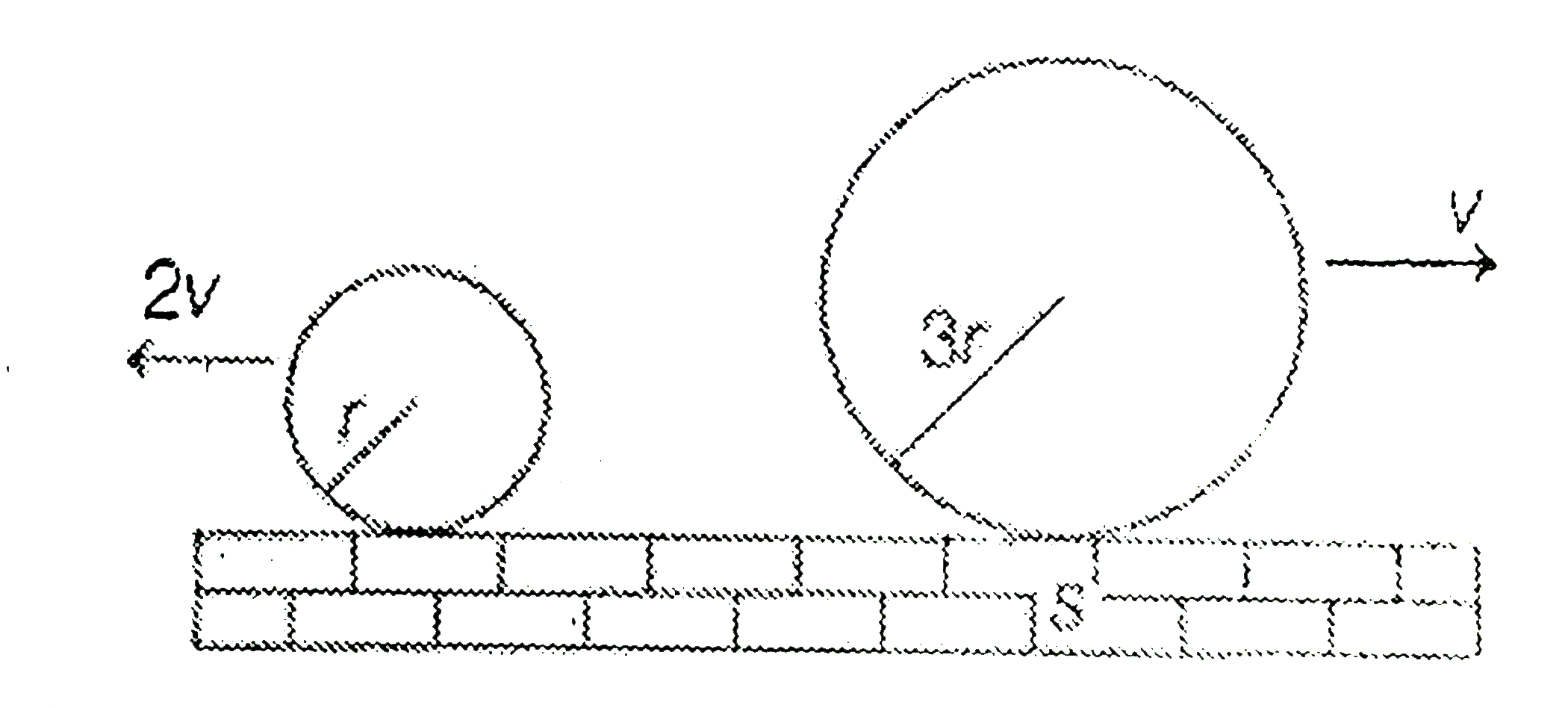AzeroB2BrvC6BrvD10Brv - Question 3 - Select One
A conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:
A2 BvRB12BvRC8BvRD4BvR
A ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will
View SolutionA vertical conduction ring of radius R falls vertically in a horizontal magnetic field of magnitude B with constant speed v . The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v , (i) A and D are at different potential
(ii) A and D are at the same potential
(iii) C and E are at the same potential
(iv) The potential difference between A and D is 2BRv , with D a higher potential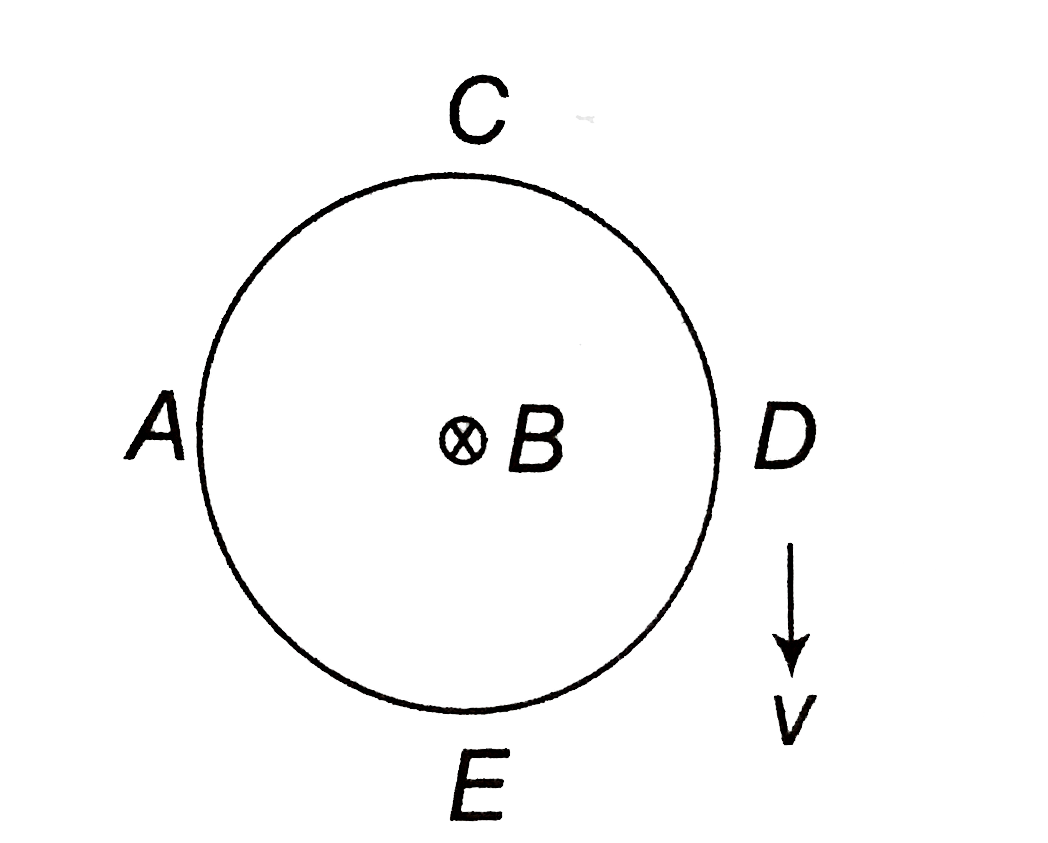
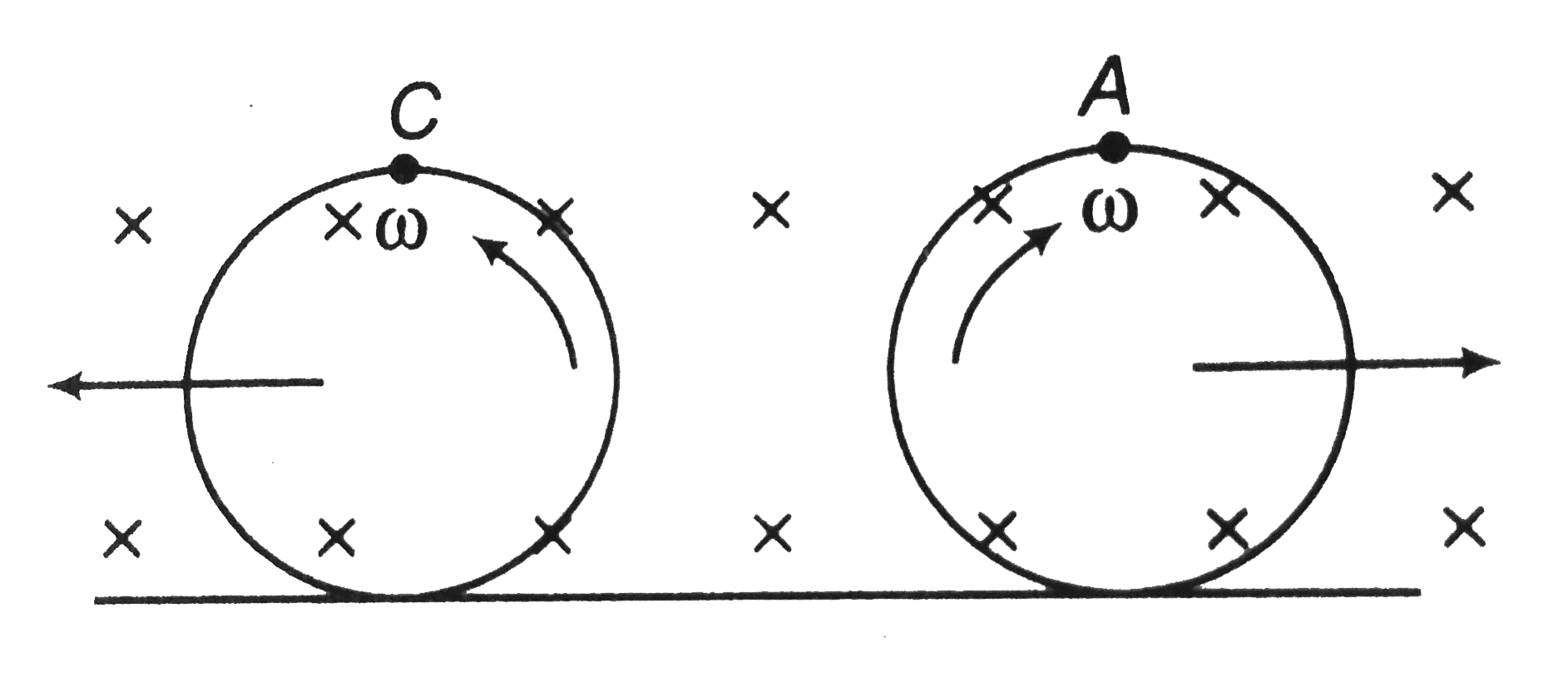
View SolutionTwo metallic rings of radius R are rolling on a metallic rod. A magnetic field of magnitude B is applied in the region. The magnitude of potential difference between points A and C on the two rings (as shown) , will be
View SolutionA conducting rod AB moves parallel to x-axis in a uniform magnetic field pointing perpendicular and into the plane of paper. The end A of the rod
View Solution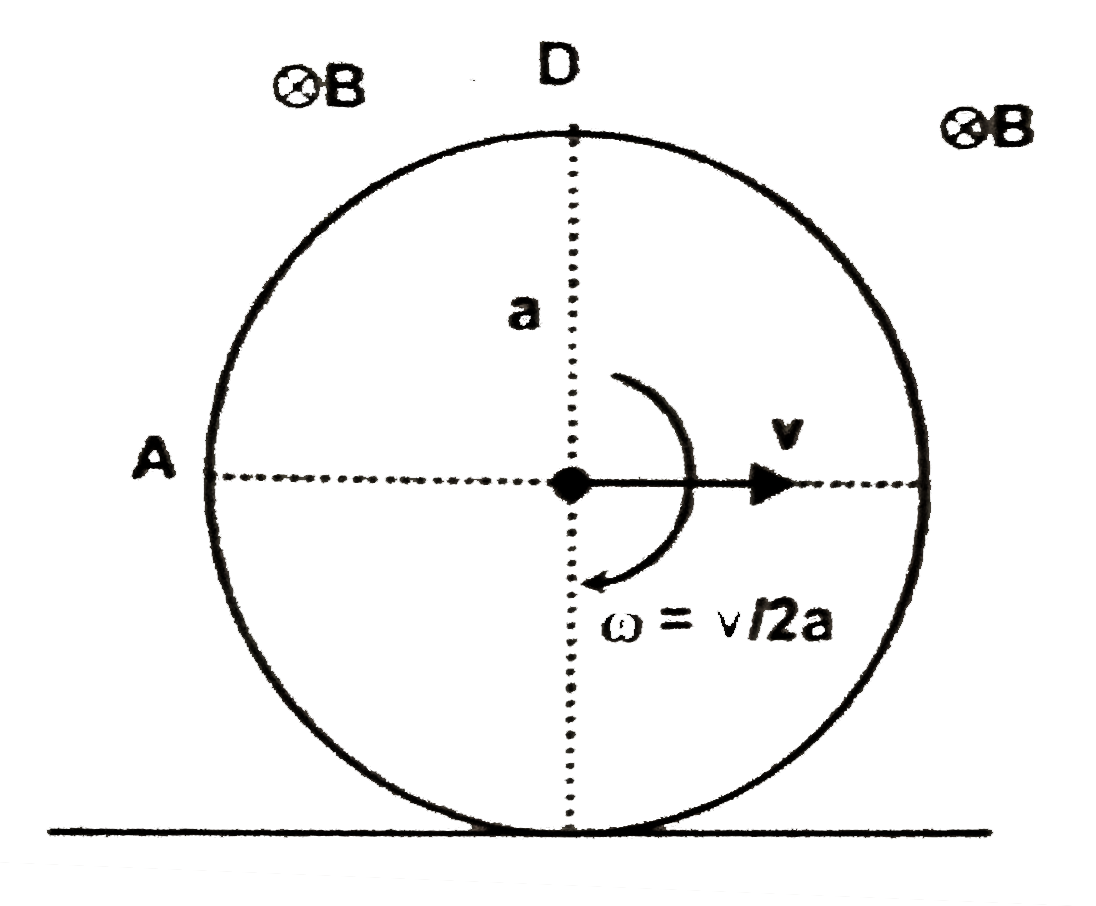
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring isView Solution