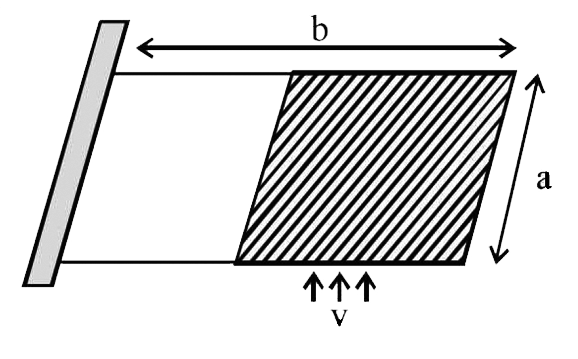
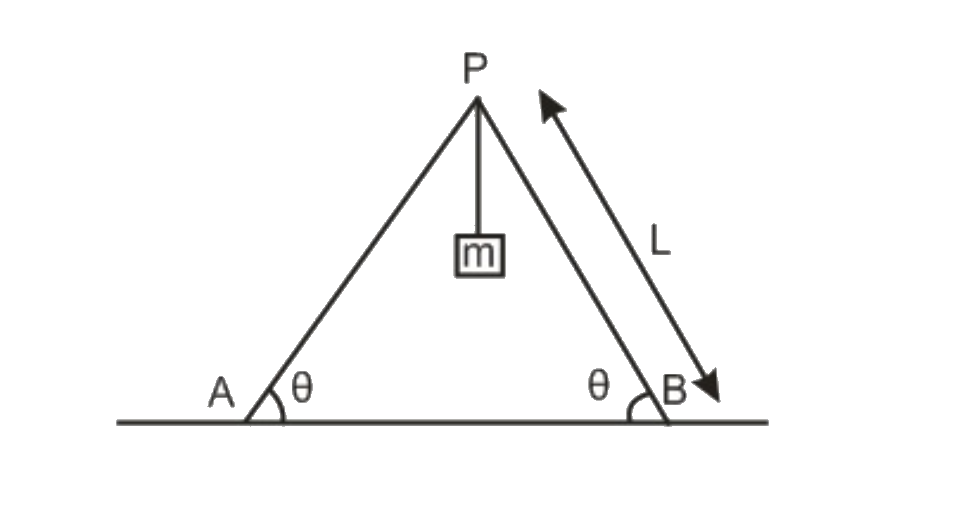
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
The correct Answer is:A, B, C
The various forces acting on the ladders are shown in the
figure.
Sicce the system is in equilibrium, therefore
rArr N = ((2M+m)g)/(2) ….(i)rArr mgxx(L)/(2)cos theta + fxxLsin theta = NL cos theta rArr f = (NL cos theta - (Mgl)/(2) cos theta)/(L sin theta)= N cot theta - (Mg)/(2) cot thetarArr f = [(2N+m)/(2))g - (Mg)/(2)]cos thetarArr f= [(M + m) (g)/(2)] cot theta
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
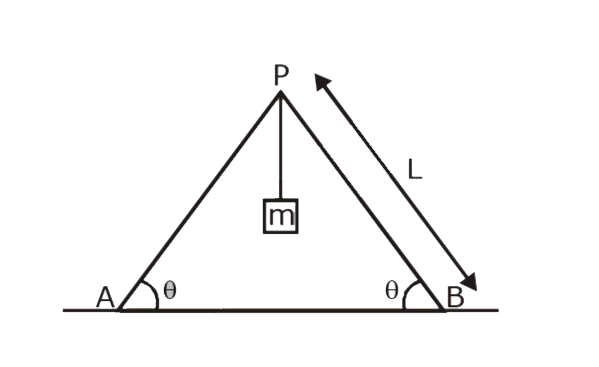
Two identical ladders are arranged as shown in the figure. Mass of each ladder is M and length L. The systemis in equilibrium. Find direction and magnitude of frictional force acting at A or B.
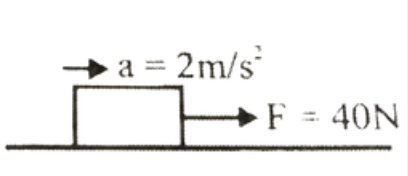
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View Solution
Knowledge Check
If the system is in equilibrium, the magnitude of friction acting on block B shown in the figure is
 A10NB18NC15NDCan not be determined
A10NB18NC15NDCan not be determinedThree blocks A,B and C are suspended as shown in the figure. Mass of each block A and C is m. if the system is in equilibrium and mass of B is M, then
 AM=2mBM<2mCM>2mDM=m.
AM=2mBM<2mCM>2mDM=m.Four blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
Two identical ladders are arranged as shown in the figure. Mass of the block is m and the mass of each ladder is M. The length of each of the ladder is L. The system is in equilibrium. What is the magnitude of frictional force acting at A or B?
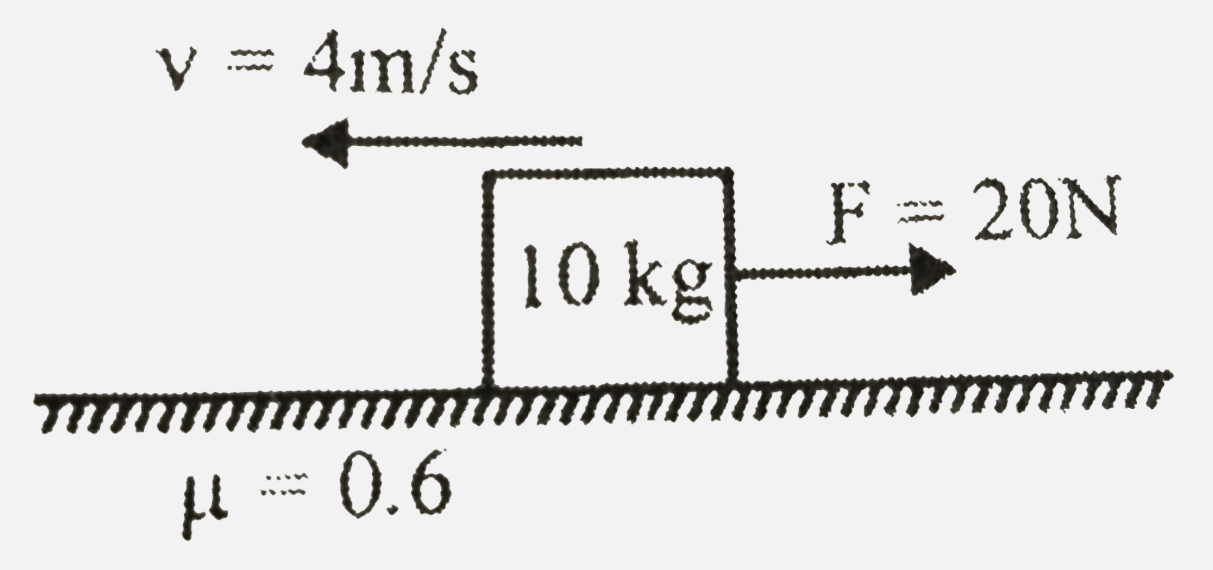
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

View Solution
