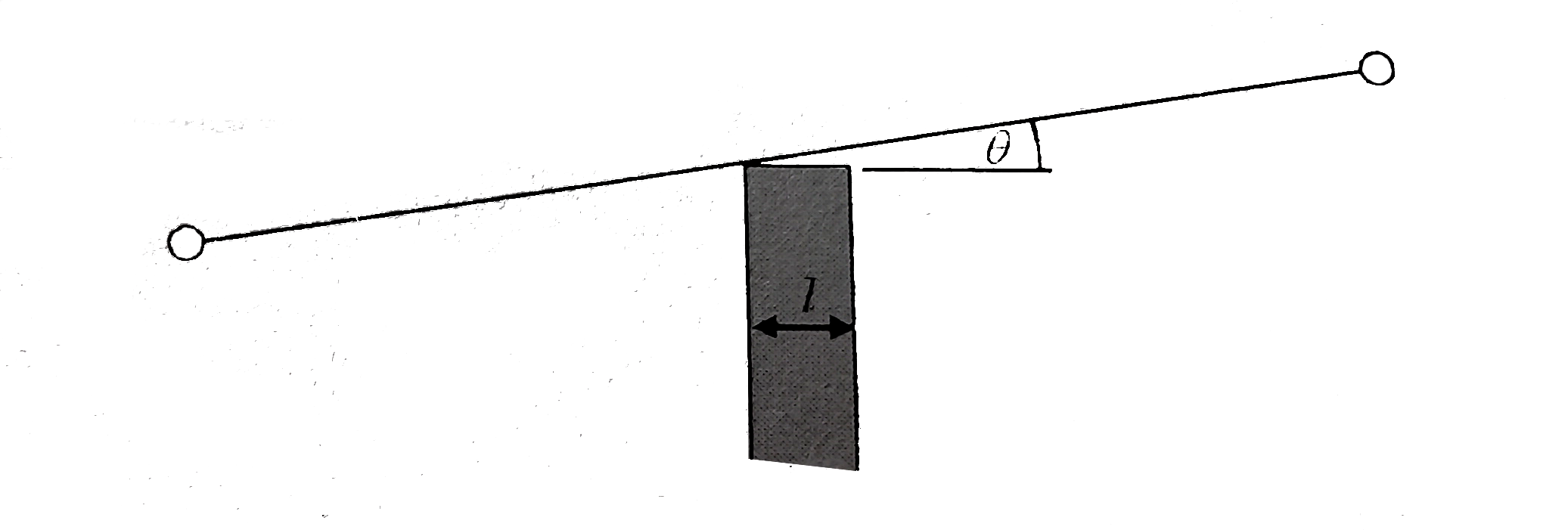
A system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

2π√√2l3g
2π√2√2l3g
2π√2l3g
3π√l3g
The correct Answer is:B
Figure
Similar Questions
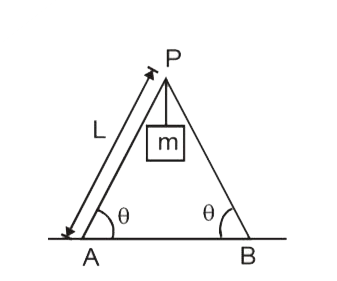
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. If the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
 View Solution
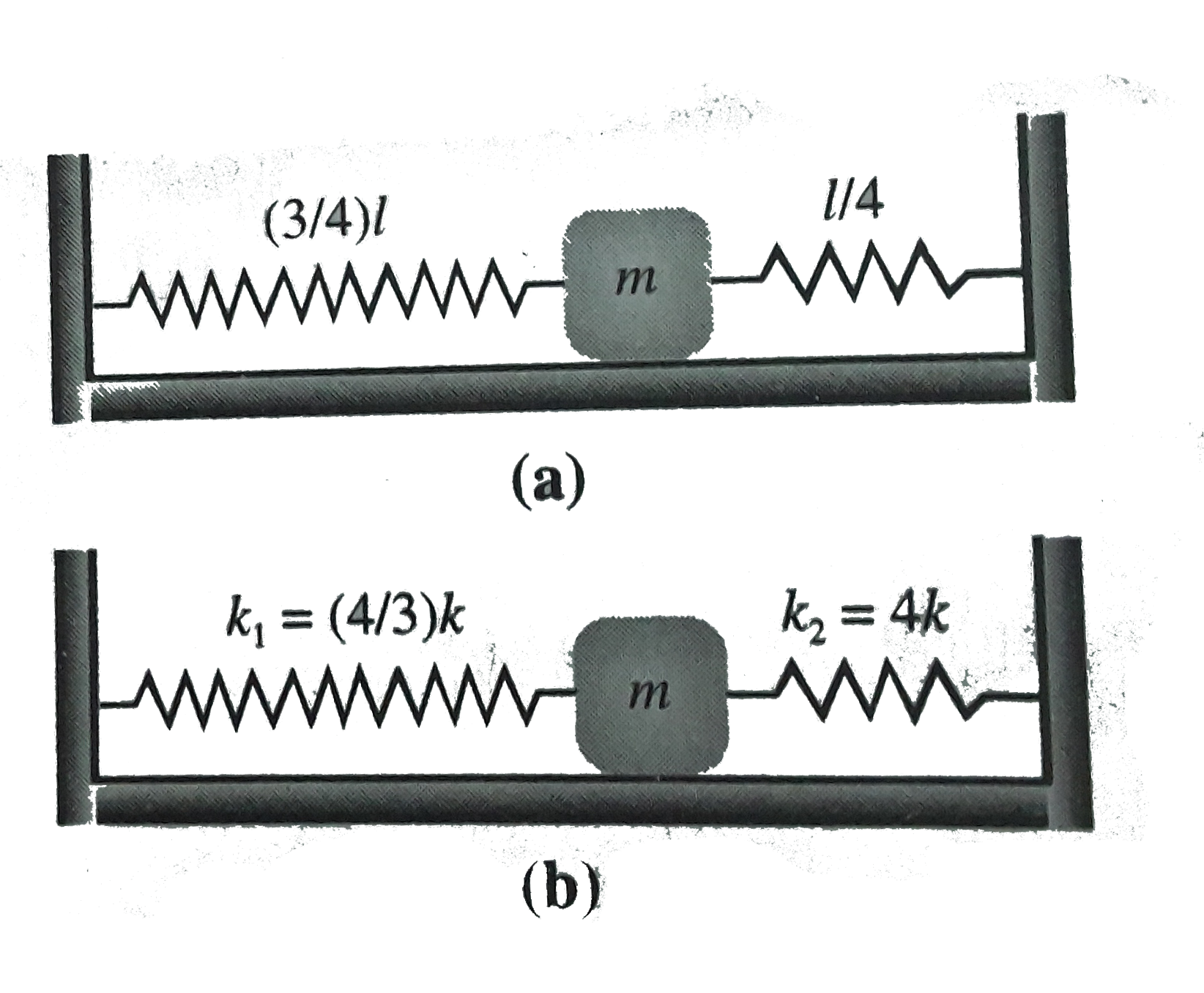
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For identical rods each of mass m and length l make a square frame in xy plane as shown. Calculate its momen of inertia about the x-axis.
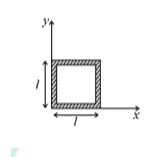 A53ml2B43ml2Cml2DNone of these
A53ml2B43ml2Cml2DNone of these - Question 2 - Select One
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
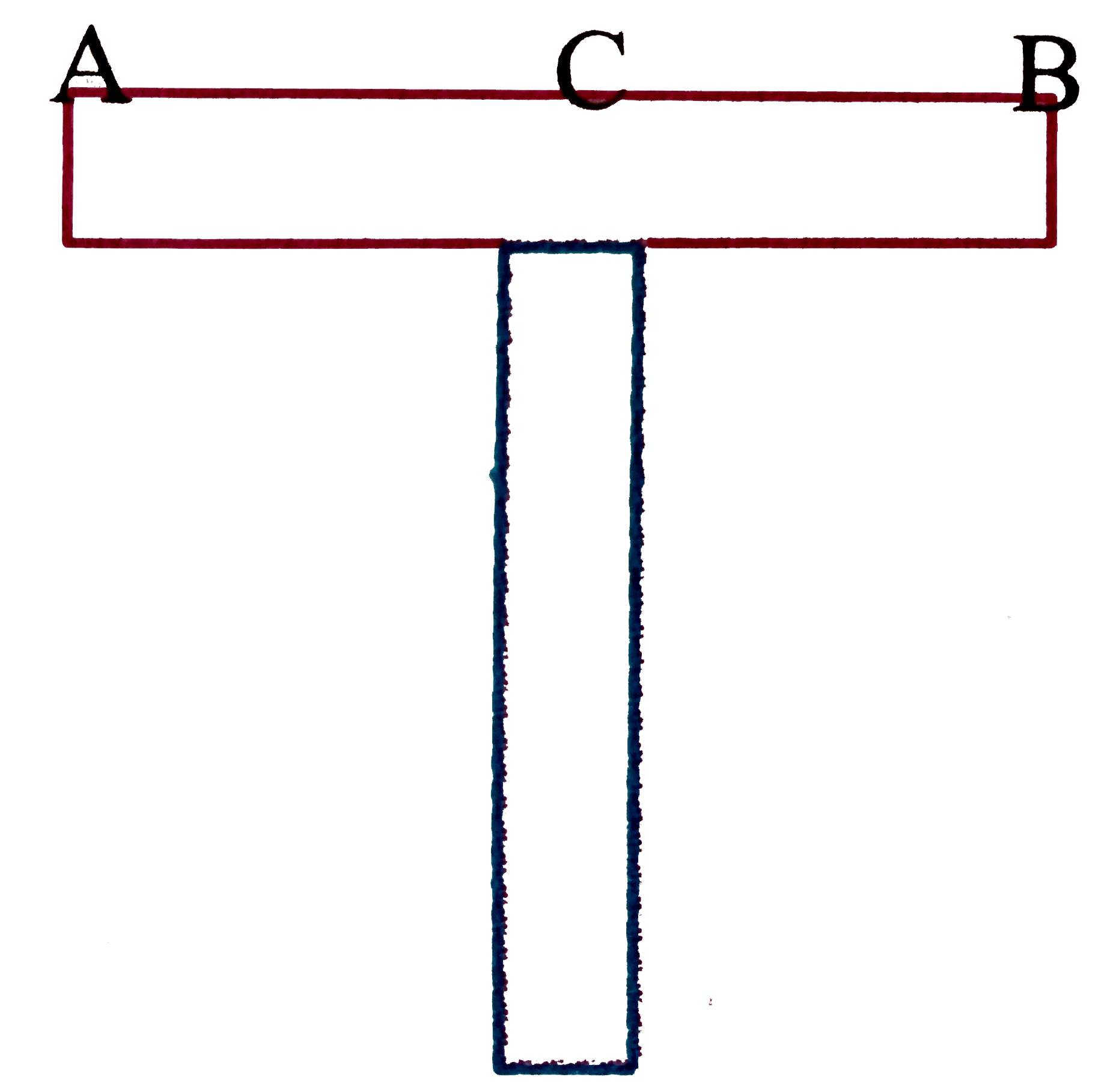 A0BL/4C3L/4DL
A0BL/4C3L/4DL - Question 3 - Select One
Four thin rods of same mass m and same length L form a square as shown in the figure. M.I. of this system about an axis through center O and perpendicular to its plane is
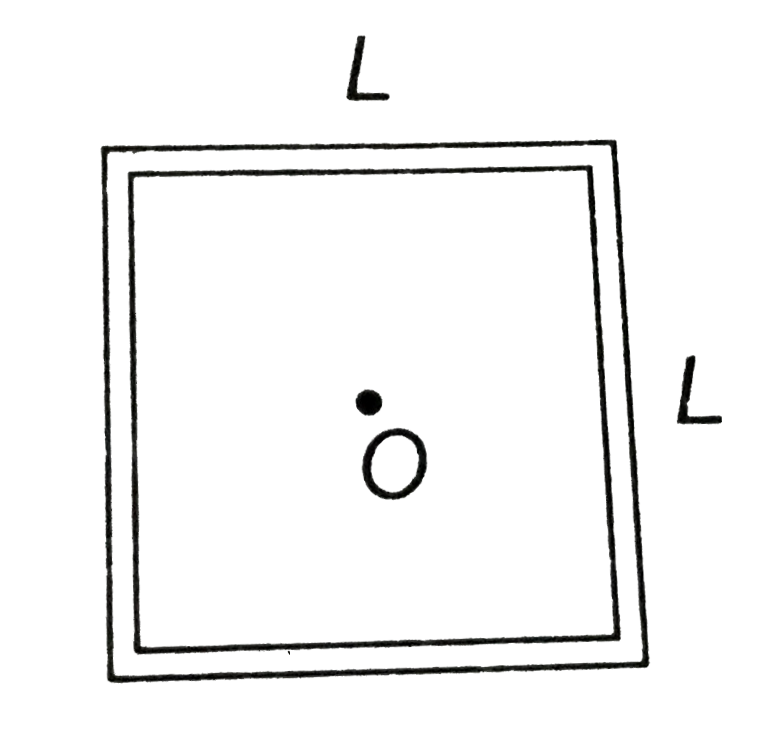 A4mL23BmL23CmL26D4mL23
A4mL23BmL23CmL26D4mL23
Two identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
 View Solution
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
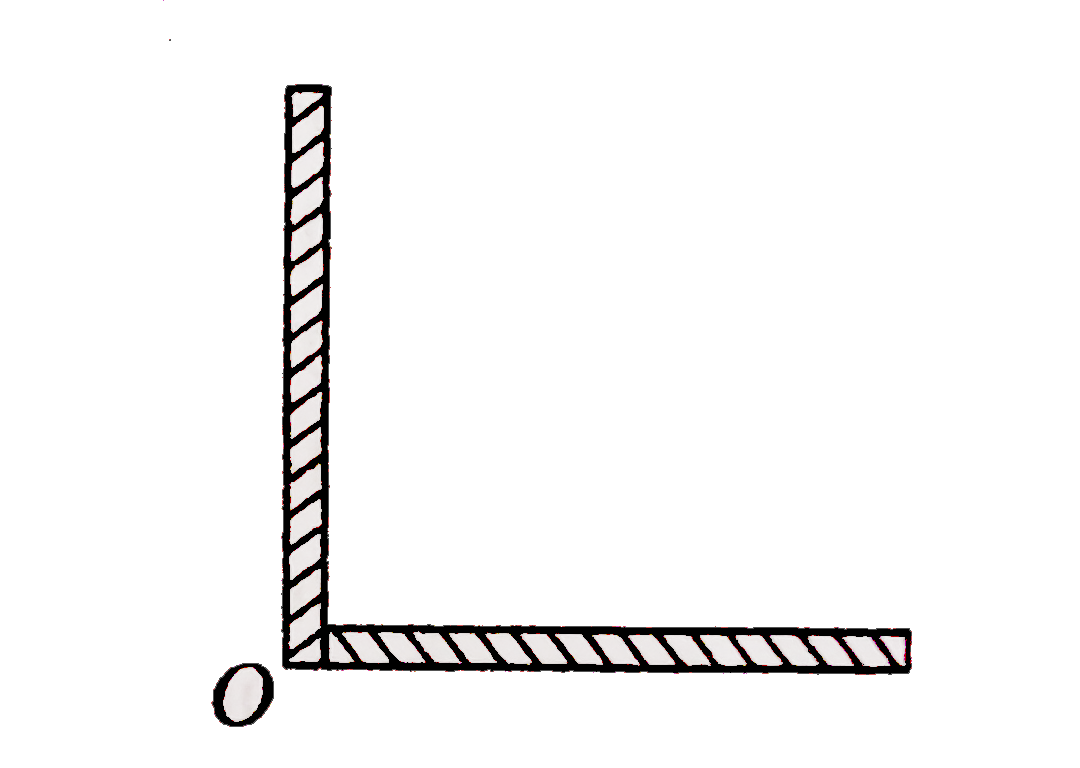 View Solution
View SolutionAn endless cord consists of lengths 2l and 2l′ and their masses per unit length are m and m′. It is placed in stable equilibrium over a smooth peg as shown in the figure. It is slightly displaced and left to itself. Show that motion is simple harmonic. Find the period of oscilattions.
 View Solution
View SolutionTwo identical small balls each of mass m are rigidly affixed at the ends of light rigid rod of length 1.5m and the assmebly is placed symmetrically on an elevated protrusion of width l as shown in the figure.
The rod-ball assmebly is titled by a small angle theta in the vertical plane as shown in the figure and released. Estimate time-period (in seconds) of the oscillation of the rod-ball assembly assuming collisions of the rod with corners of the protrusion to be perfectly elastic and the rod does not slide on the corners. Assume θ=gl (numerically in radians), where g is the acceleration of free fall.
 View Solution
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod isView Solution

