Two identical metal plates are given poistive charges Q1 and Q2 (<Q1) respectively. If they are now brought close together to form a parallel plate capacitor with capacitance C, the potencial difference between them is
(Q1+Q2)/2C
(Q1+Q2)/C
(Q1−Q2)/C
(Q1−Q2)/2C
To solve the problem of finding the potential difference between two identical metal plates with charges Q1 and Q2 (where Q1>Q2), we can follow these steps:
Step 1: Understand the Configuration
We have two parallel plates, one with charge Q1 and the other with charge Q2. The area of each plate is A, and the separation between the plates is D.
Hint: Visualize the setup of the parallel plates and the charges on them.
Step 2: Calculate the Electric Field
The electric field E between two plates can be derived from the charges on the plates. The electric field due to a single plate with charge Q is given by the formula:
E=Q2ϵ0A
where ϵ0 is the permittivity of free space.
For the two plates:
- The electric field due to plate 1 (charge Q1) is:
E1=Q12ϵ0A
- The electric field due to plate 2 (charge Q2) is:
E2=Q22ϵ0A
Hint: Remember that the electric fields due to the plates will add up in the region between them.
Step 3: Determine the Net Electric Field
The net electric field E between the plates is the difference between the two electric fields:
E=E1−E2=Q12ϵ0A−Q22ϵ0A
This simplifies to:
E=Q1−Q22ϵ0A
Hint: Pay attention to the signs of the electric fields; they can affect the direction of the net field.
Step 4: Calculate the Potential Difference
The potential difference V between the plates is given by the product of the electric field and the distance D between the plates:
V=E⋅D
Substituting the expression for E:
V=(Q1−Q22ϵ0A)⋅D
Hint: Make sure to keep track of the units when calculating potential difference.
Step 5: Relate Capacitance to Potential Difference
The capacitance C of the parallel plate capacitor is defined as:
C=ϵ0AD
We can rearrange this to express D in terms of C:
D=ϵ0AC
Substituting this back into the equation for V:
V=Q1−Q22ϵ0A⋅ϵ0AC
This simplifies to:
V=Q1−Q22C
Final Answer
Thus, the potential difference V between the plates is:
V=Q1−Q22C
---
We have two parallel plates, one with charge Q1 and the other with charge Q2. The area of each plate is A, and the separation between the plates is D.
The electric field E between two plates can be derived from the charges on the plates. The electric field due to a single plate with charge Q is given by the formula:
E=Q2ϵ0A
where ϵ0 is the permittivity of free space.
- The electric field due to plate 1 (charge Q1) is:
E1=Q12ϵ0A
- The electric field due to plate 2 (charge Q2) is:
E2=Q22ϵ0A
The net electric field E between the plates is the difference between the two electric fields:
E=E1−E2=Q12ϵ0A−Q22ϵ0A
This simplifies to:
E=Q1−Q22ϵ0A
The potential difference V between the plates is given by the product of the electric field and the distance D between the plates:
V=E⋅D
Substituting the expression for E:
V=(Q1−Q22ϵ0A)⋅D
The capacitance C of the parallel plate capacitor is defined as:
C=ϵ0AD
We can rearrange this to express D in terms of C:
D=ϵ0AC
V=Q1−Q22ϵ0A⋅ϵ0AC
This simplifies to:
V=Q1−Q22C
Thus, the potential difference V between the plates is:
V=Q1−Q22C
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
If a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionA charge of 20 microCoulomb is placed on the positive plate of on isolated parallel - plate capacitor of capacitance 10microFarad calculate the potential difference developed between the plates .
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
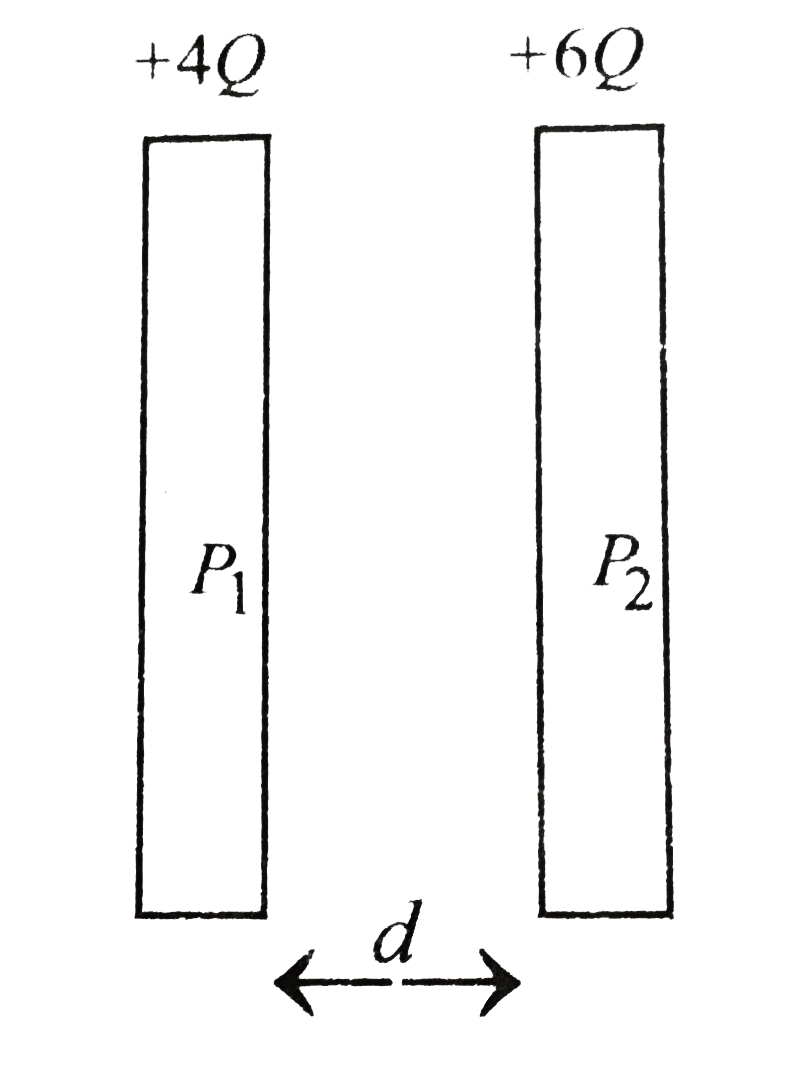 View Solution
View SolutionCharges 2q and −3q are given to two identical metal plates of area of cross section A. the distance between the plates is d. Find the capacitance and potential difference between the plates.
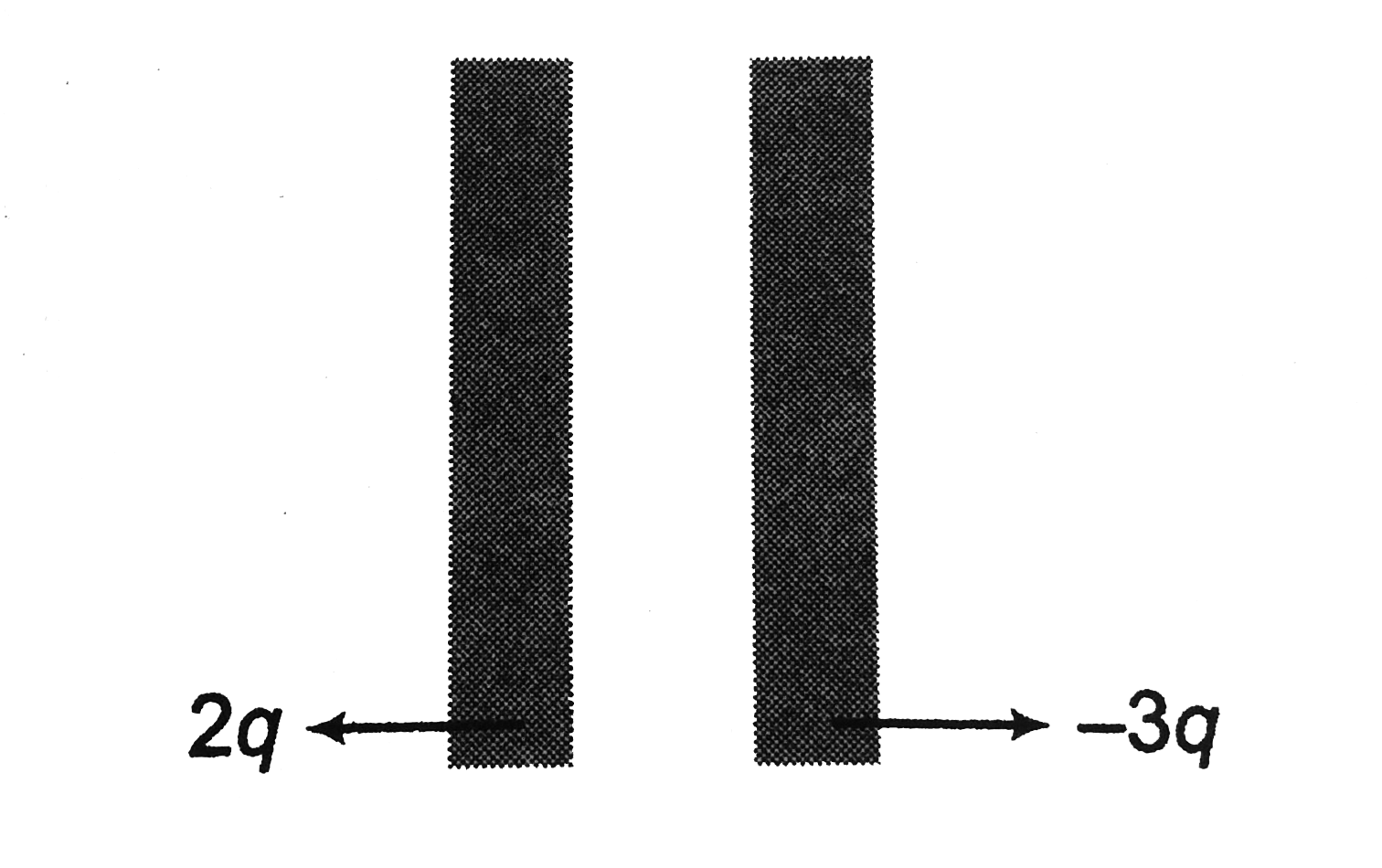 View Solution
View SolutionTwo identical small conducting balls have positive charges q1 and q2 respectively. The force between the balls when they are placed at a separation is F. The balls are brought together so that they touch and then put back in their original positions. Prove that the force between the balls now, cannot be less than F.
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png) View Solution
View SolutionA charge of 1μC is given to one plate of a parallel - plate capacitor of capacitance 0.1μF and a charge of 2μC is given to the other plate . Find the potential difference developed between the plate .
View SolutionEach plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is
 View Solution
View Solution
