Two identical small equally charged conducting balls are suspended from long threads secured at one point. The charges and masses of the balls are such that they are in equilibrium when the distance between them is a(the length of thread L>>a). Then one of the balls is discharged. what will be the distance b(b<<L) between the balls when equilibrium is restored?
The correct Answer is:4
To solve the problem step-by-step, we will analyze the forces acting on the charged balls and apply the principles of equilibrium and electrostatics.
Step 1: Understand the Initial Setup
We have two identical small conducting balls, each with charge q, suspended from a common point by threads of length L. Initially, they are in equilibrium at a distance a apart. The forces acting on each ball are:
- The gravitational force mg acting downward.
- The tension T in the thread acting along the thread.
- The electrostatic force Fe acting horizontally due to the repulsion between the two charges.
Step 2: Analyze the Forces
In equilibrium, the vertical and horizontal components of the forces must balance.
1. Vertical Forces:
Tcosθ=mg(1)
2. Horizontal Forces:
Tsinθ=Fe=kq2a2(2)
where k is Coulomb's constant.
Step 3: Relate the Angles to the Distances
Using the geometry of the situation, we can express sinθ and cosθ in terms of a and L:
- From the triangle formed, we have:
sinθ≈a/2L(for small angles)
cosθ≈1(for small angles)
Step 4: Substitute and Simplify
Substituting sinθ and cosθ into the equations (1) and (2):
1. From (1):
T=mgcosθ≈mg
2. From (2):
Tsinθ=mgL⋅a/2L=kq2a2
Step 5: Find the Relationship Between a and L
Using the two equations, we can derive a relationship:
mg⋅a/2Lmg=kq2a2
This simplifies to:
a32L=kq2mg
Let’s denote this as Equation (1).
Step 6: Discharge One Ball
When one ball is discharged, it loses its charge, and the other ball retains a charge q. The charge on the discharged ball becomes 0, and the remaining ball will have a charge of q2 when they touch and share charge.
Step 7: New Equilibrium Condition
After the discharge, we need to find the new distance b between the balls when they come to equilibrium again. The new electrostatic force is:
F′e=k(q2)2b2=kq24b2
Using similar force balance as before:
1. Vertical Forces:
T′cosθ′=mg(3)
2. Horizontal Forces:
T′sinθ′=kq24b2(4)
Step 8: Substitute and Relate b and a
Using the same approach as before, we can write:
mg⋅b/2Lmg=kq24b2
This simplifies to:
b32L=kq24mg
Let’s denote this as Equation (2).
Step 9: Divide Equations (1) and (2)
Dividing Equation (2) by Equation (1):
b3/2La3/2L=kq2/4mgkq2/mg
This simplifies to:
b3a3=14
Thus:
b3=a34
Taking the cube root:
b=a√(3)4=a22/3
Final Answer
The distance b between the balls when equilibrium is restored is:
b=a22/3
We have two identical small conducting balls, each with charge q, suspended from a common point by threads of length L. Initially, they are in equilibrium at a distance a apart. The forces acting on each ball are:
- The gravitational force mg acting downward.
- The tension T in the thread acting along the thread.
- The electrostatic force Fe acting horizontally due to the repulsion between the two charges.
In equilibrium, the vertical and horizontal components of the forces must balance.
Tcosθ=mg(1)
Tsinθ=Fe=kq2a2(2)
where k is Coulomb's constant.
Using the geometry of the situation, we can express sinθ and cosθ in terms of a and L:
- From the triangle formed, we have:
sinθ≈a/2L(for small angles)
cosθ≈1(for small angles)
Substituting sinθ and cosθ into the equations (1) and (2):
1. From (1):
T=mgcosθ≈mg
Tsinθ=mgL⋅a/2L=kq2a2
Using the two equations, we can derive a relationship:
mg⋅a/2Lmg=kq2a2
This simplifies to:
a32L=kq2mg
Let’s denote this as Equation (1).
When one ball is discharged, it loses its charge, and the other ball retains a charge q. The charge on the discharged ball becomes 0, and the remaining ball will have a charge of q2 when they touch and share charge.
After the discharge, we need to find the new distance b between the balls when they come to equilibrium again. The new electrostatic force is:
F′e=k(q2)2b2=kq24b2
1. Vertical Forces:
T′cosθ′=mg(3)
T′sinθ′=kq24b2(4)
Using the same approach as before, we can write:
mg⋅b/2Lmg=kq24b2
This simplifies to:
b32L=kq24mg
Let’s denote this as Equation (2).
Dividing Equation (2) by Equation (1):
b3/2La3/2L=kq2/4mgkq2/mg
This simplifies to:
b3a3=14
Thus:
b3=a34
Taking the cube root:
b=a√(3)4=a22/3
The distance b between the balls when equilibrium is restored is:
b=a22/3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type20videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answers Type2videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension25videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
Two identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
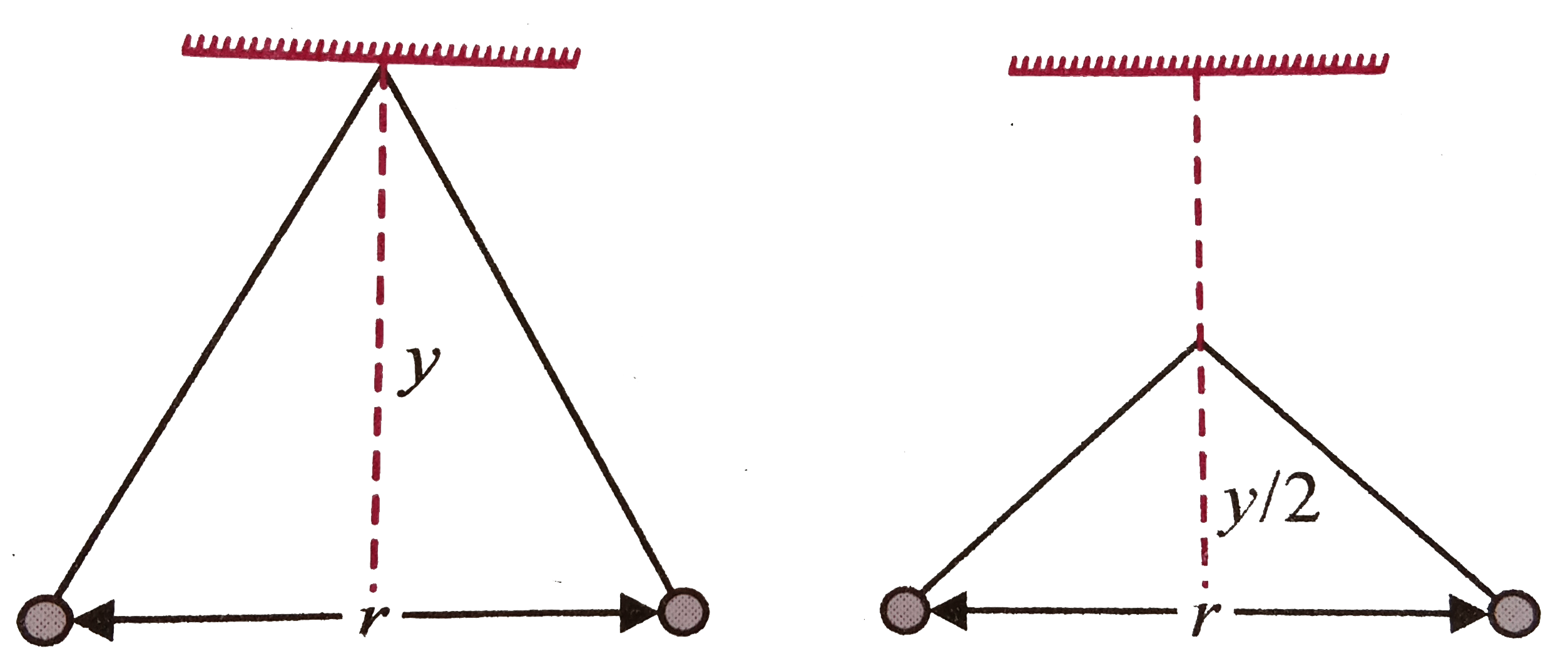 View Solution
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
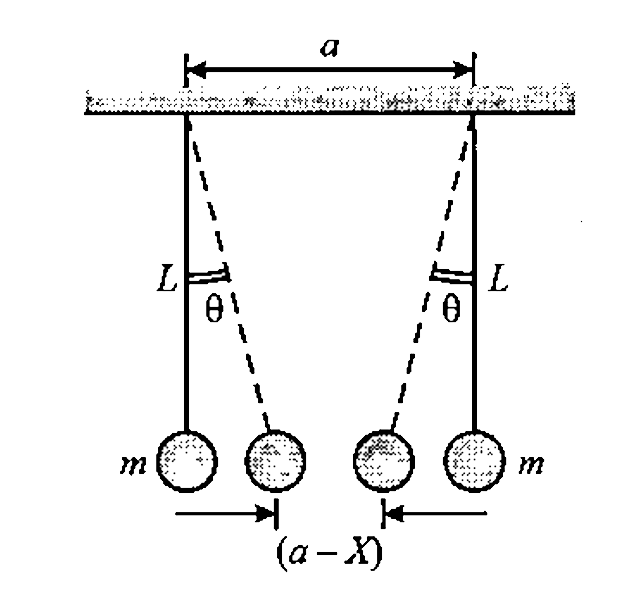 View Solution
View SolutionTwo identical metals balls with charges +2Q and −Q are separated by some distance and exert a force F on each other . They are joined by a conducting wire , which is then removed. The force between them will now be
View SolutionThree identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of l=20cm . What charges should be imparted to the balls for each thread to form an angle of α=30∘ with the vertical?
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo pitch balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become
 View Solution
View Solutiontwo pith balls each with mass m are suspended from insulating threads. When the pith balls are given equal positive charge Q, they hang in equilibirum as shown. We now increase the charge on the left pith ball from Q to 2Q while leaving its mass essentially unchanged. Which of he following diagrams best represent the new equilibrium configuration?
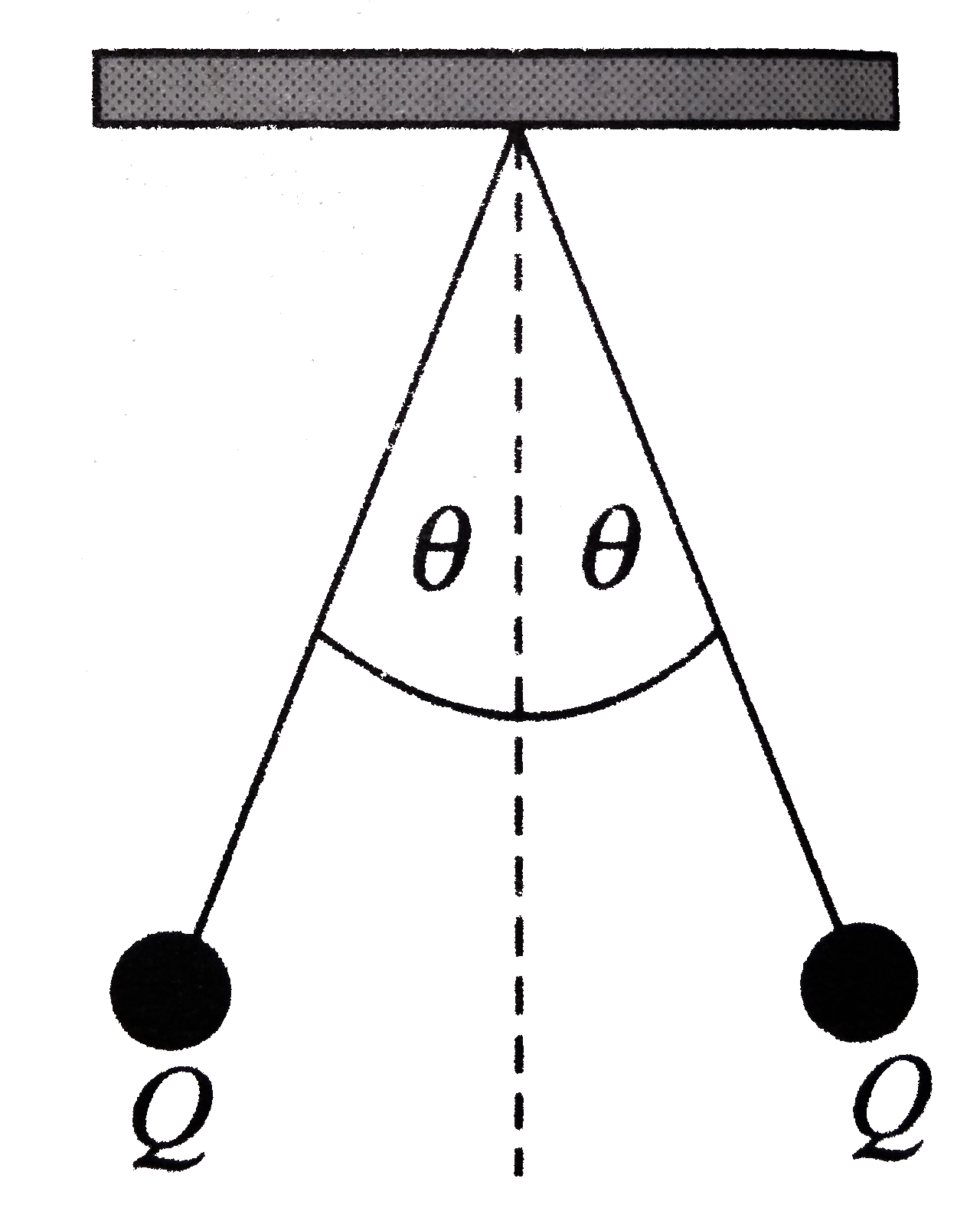 View Solution
View SolutionA ball is dropped downwards . After 1 second another ball is dropped downwards from the same point . What is the distance between them after 3 seconds .
View Solution

