Question

A ring of radius R has charge $-Q$ distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at a point on the axis of the ring at distant R from the center of the ring.

Answer

2

Explanation

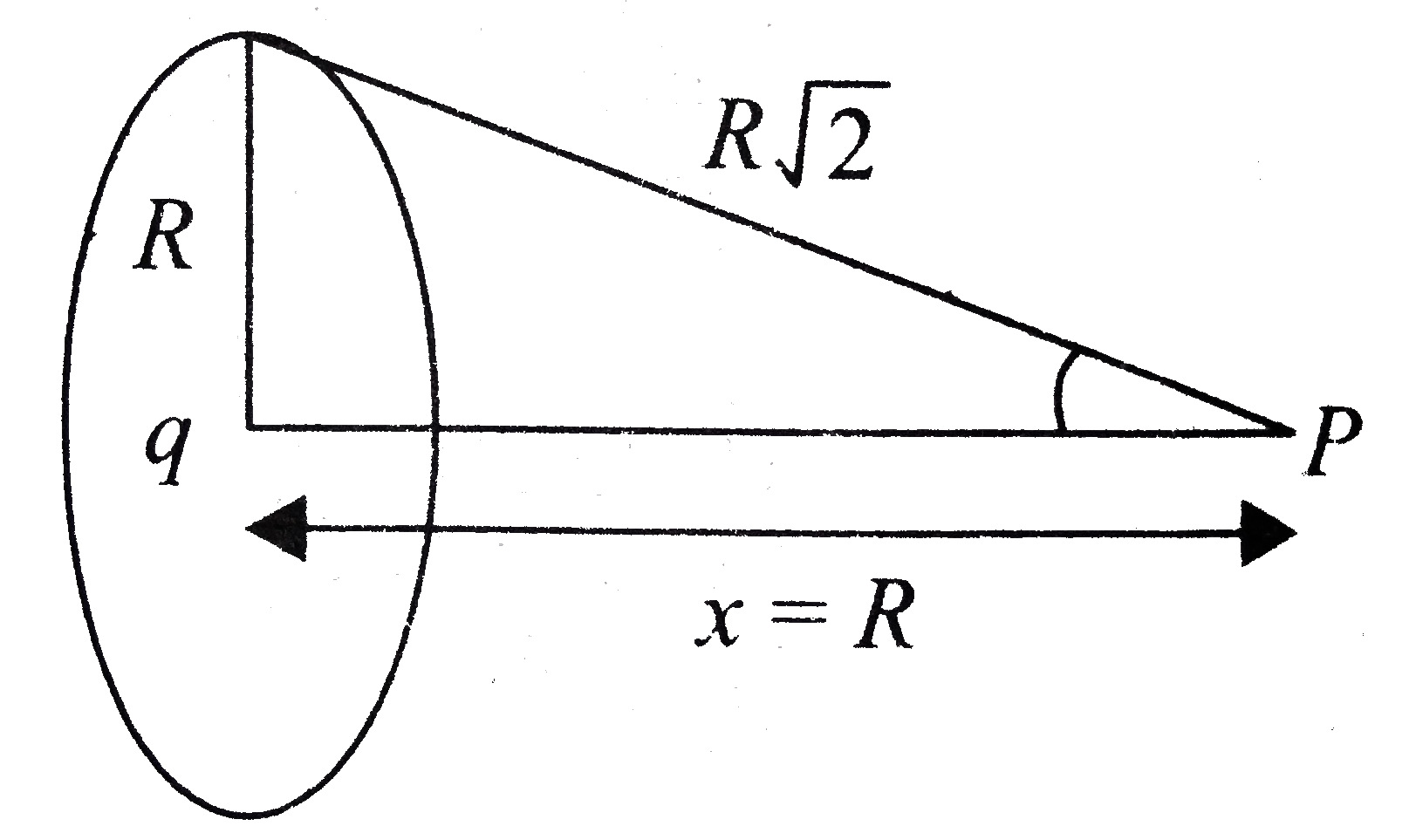
Electric field at point P due to charge of ring is
`E=(kQx)/((R^(2)+x^(2))^(3//2))`
At x=R, `E=(kQ)/(2 sqrt(2)R^(2))` directed toward the center
Electric fild at P due to charge at center , `kq//R^(2)`.
For net field to be zero at P
`(kq)/(R^2)=(kQ)/(2 sqrt(2)R^(2))` or `q=(Q)/(2 sqrt(2))=(Q)/(4)sqrt(2)`.