Two identical springs A and B each of spring constant K are attached to a block of mass M and to two fixed supports as shown in the figure. When the mass M is displaced through a small dis"tan"ce from its equilibrium position, it executes a S.H.M. What is its frequency of oscillation ?

n=12π√KM
n=12π√K2M
n=12π√2KM
n=12π√K2M
The correct Answer is:C
If the mass M is displaced to the right through a small dis"tan"ce x towards right, the spring A gets elongated by a dis"tan"ce x.
∴ Restoring force due to A is F = - Kx towards left.
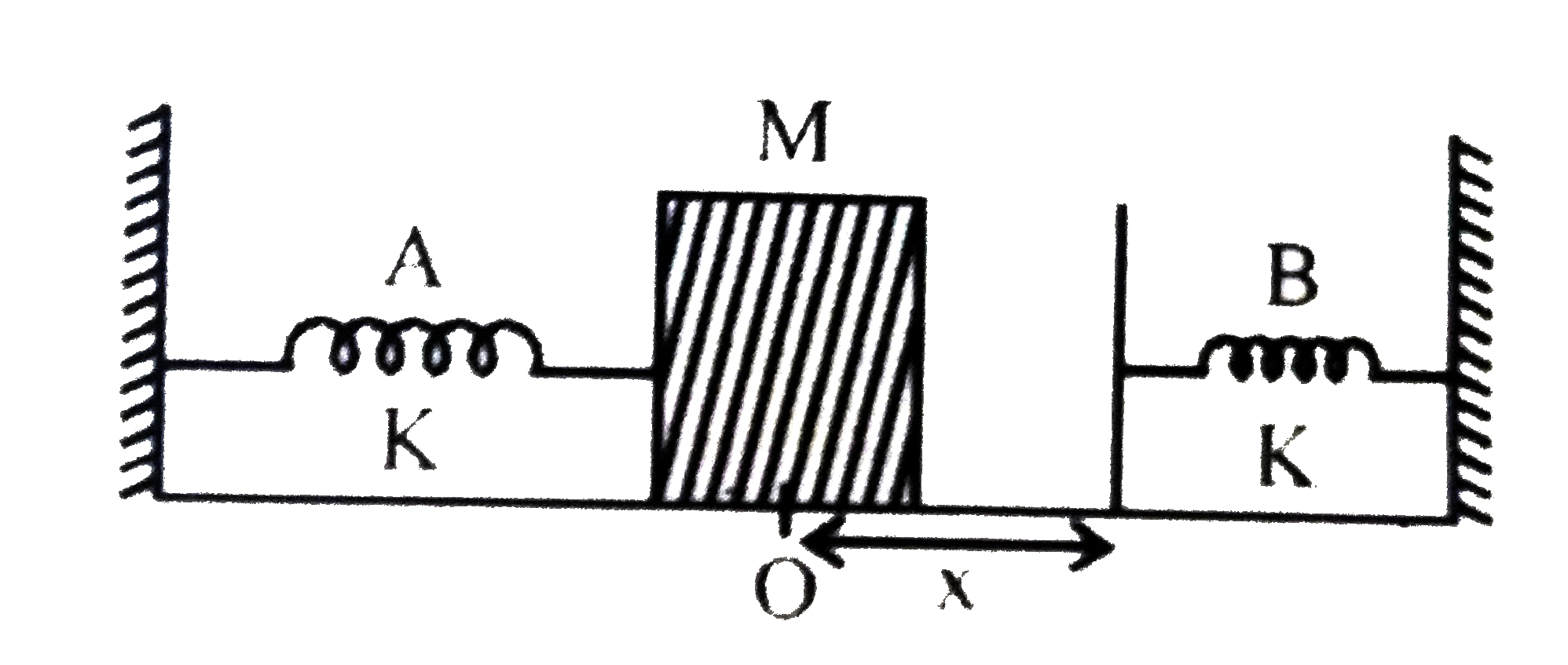
The spring B gets compressed by a dis"tan"ce x
∴ Restoring force due to B is F2=−Kx towards left. Thus both forces are acting towards left.
∴ The net force F=F2+F2=−2Kx and the spring constant of the system =2K as F= - 2Kx.
The mass M M performs a SHM of frequency
n=12π√K'M=12π√2KM
Topper's Solved these Questions
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
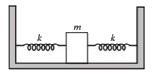 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
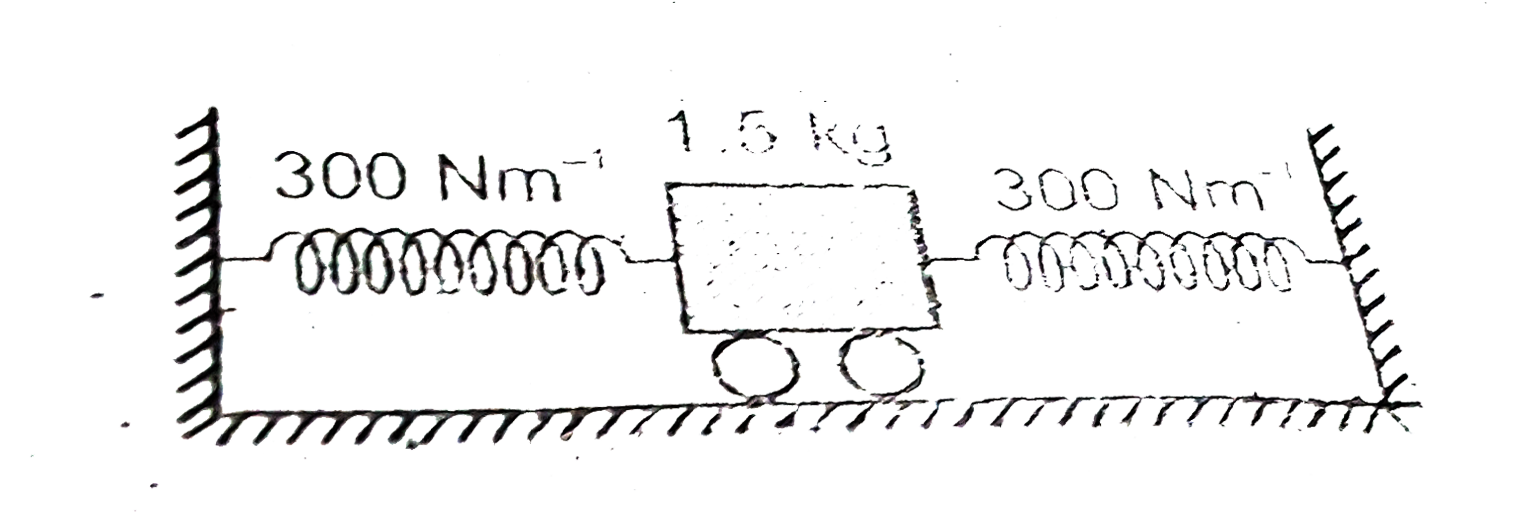
View Solution
