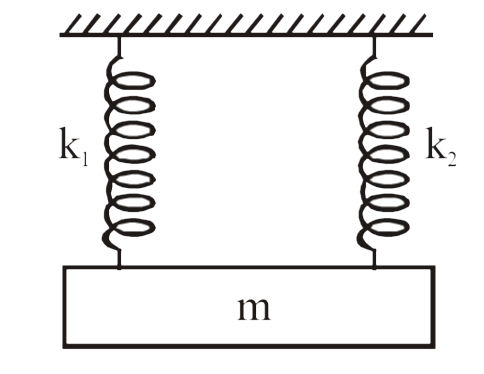
A mass $m$ is suspended separately by two different spring of spring constant $K_{1}$ and $k_{2}$ given the time period $t_{1}$ and $t_{2}$ respectively if the same mass $m$ is shown in the figure then time period $t$ is given by the relation

A

$t = \frac{t_{1} t_{2}}{t_{1} + t_{2}}$

B

$t^{2} = t_{1}^{2} + t_{2}^{2}$

C

$t = t_{1} + t_{2}$

D

$t^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$t_{1} = 2 π \sqrt{\frac{m}{K_{1}}} ∴ t_{1}^{2} = 4 π^{2} \frac{m}{K_{1}}$
$∴ K_{1} = \frac{4 π_{m}^{2}}{t_{1}^{2}}$
and $t_{2} = 2 π \sqrt{\frac{m}{K_{2}} ∴ t_{2}^{2} = 4 π^{2} \frac{m}{K_{2}}}$
$∴ K_{2} = \frac{4 π_{m}^{2}}{t_{2}^{2}}$
and when they are joined in parallel, $K = K_{1} + K_{2}$
and $t = 2 π \sqrt{\frac{m}{K_{1} + K_{2}} ∴ t^{2} = 4 π^{2} \frac{m}{(K_{1} + K_{2})}}$
and $K_{1} + K_{2} = \frac{4 π^{2} m}{t^{2}}$
$∴$ from (1), (2) and (3),
$\frac{4 π^{2} m}{t^{2}} = \frac{4 π^{2} m}{t_{1}^{2}} + \frac{4 π^{2} m}{t_{2}^{2}}$
$∴ t^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$

|

Updated on:21/07/2023

Class 12 PHYSICS OSCILLATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A mass is suspended separately by two different springs in successive order then time periods is $t_{1}$ and $t_{2}$ respectively. If it is connected by both spring as shown in figure then time period is to, the correct relation is

A $t_{0}^{2} = t_{1}^{2} + t_{2}^{2}$
B $t_{0}^{- 2} = t_{1}^{- 2} + t_{2}^{- 2}$
C $t_{0}^{- 1} = t_{1}^{- 1} + t_{2}^{- 1}$
D $t_{0} = t_{1} + t_{2}$
Question 2 - Select One
A mass is suspended separately by two springs of spring constants $k_{1}$ and $k_{2}$ in successive order. The time periods of oscillations in the two cases are $T_{1}$ and $T_{2}$ respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

A $T^{2} = T_{1}^{2} + T_{2}^{2}$
B $T^{- 2} = T_{1}^{- 2} + T_{2}^{- 2}$
C $T^{- 1} = T_{1}^{- 1} + T_{2}^{- 1}$
D $T = T_{1} + T_{2}$
Question 3 - Select One
When a block of mass m is suspended separately by two different springs have time period $t_{1} and t_{2}$ . If same mass is connected to parallel combination of both springs, then its time period is given by :-
A $\frac{t_{1} t_{2}}{t_{1} + t_{2}}$
B $\frac{t_{1} t_{2}}{\sqrt{t_{1}^{2} + t_{2}^{2}}}$
C $\sqrt{\frac{t_{1} t_{2}}{t_{1} + t_{2}}}$
D $t_{1} + t_{2}$

MARVEL PUBLICATION-OSCILLATIONS-MCQ

Home
Ask Doubt
Profile