Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

Let the mass be displaced by a small distance x to the right side of the equilibrium position, as shown in Fig. 14.15. Under this situation the spring on the left side gets
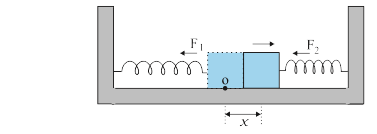
elongated by a length equal to x and that on the right side gets compressed by the same length. The forces acting on the mass are then,
(force exerted by the spring on the left side, trying to pull the mass towards the mean position)
(force exerted by the spring on the right side, trying to push the mass towards the mean position) The net force, F, acting on the mass is then given by,
Hence the force acting on the mass is proportional to the displacement and is directed towards the mean position, therefore, the motion executed by the mass is simple harmonic. The time period of oscillations is,
Topper's Solved these Questions
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View Solution
Knowledge Check
Two springs of spring constant 6N/m and 4N/m are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider √10=π)A1sB2sC0.5sD4sA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
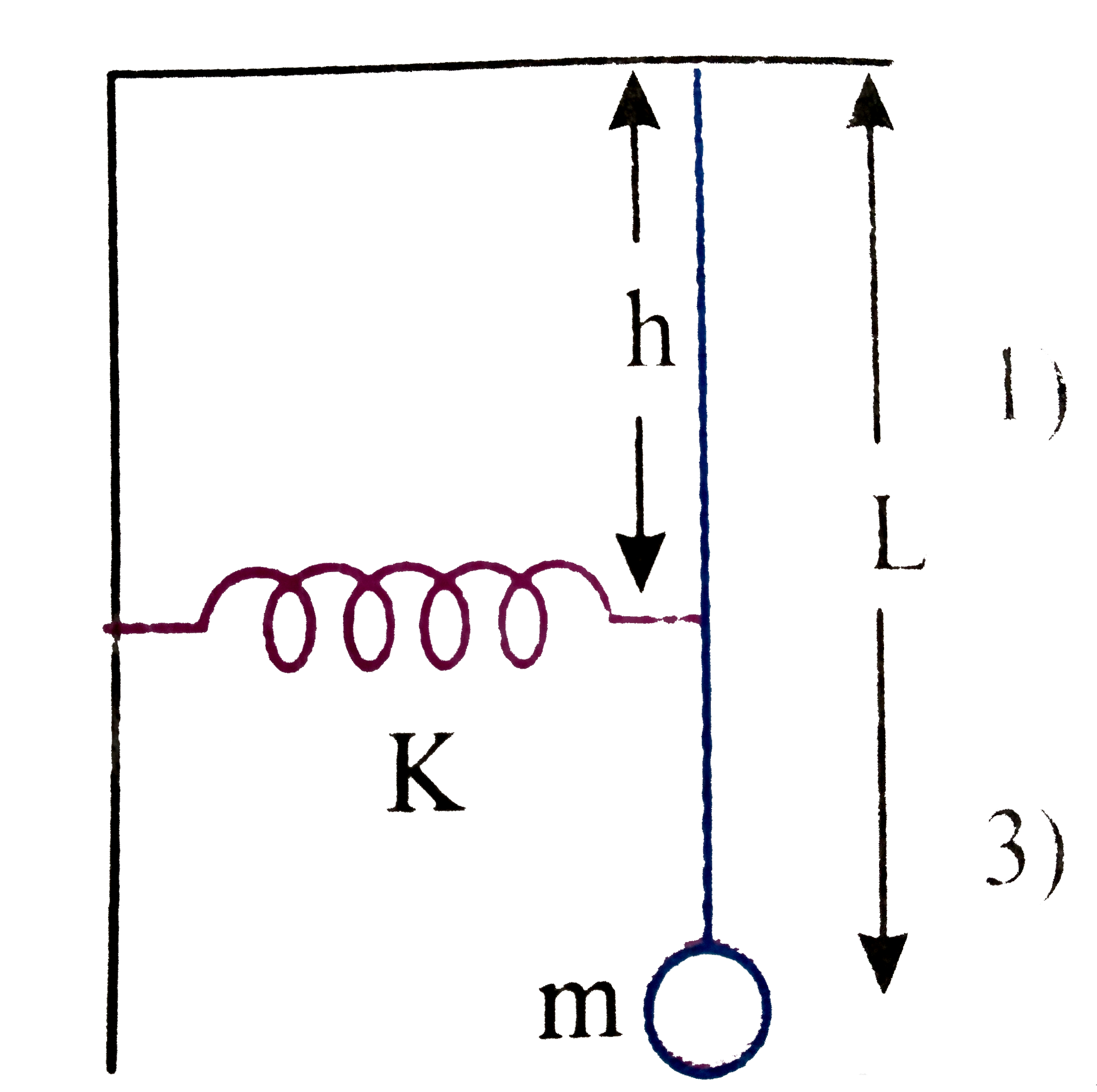 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFigure shows the graph of velocity versus displacement of a partciel executing simple harmonic motion. Find the period of oscillation of the particle.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View Solution
