Two identical stars of mass M orbit around their centre of mass. Each orbit is circular and has radius R, so that the two stars are always on opposite of the circle.
(a) Find the gravitational force of one star on the other.
(b) Find the orbital speed of each star and the period of the orbit.
(c ) What minimum energy would be required to separate the two stars to infinity?
The correct Answer is:B, C, D
F=GM.M(2R)2=Gm24R2

(b) GM24R2=MV2R
∴Nu=√GM4R
T=2π(R)ν=2πR√GM/4R=4πR3/2√GM (c ) W=Ef−Ei=[Uf−Ui]+[Kf−Ki]
=[0−(−GMM2R)]+[0−2×12×M(√GM4R)2]
=GM24R
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct
27 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
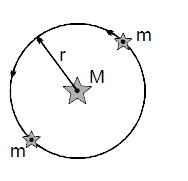
View SolutionThree identical stars of mass M form an equilateral triangle that rotates around the triangle's center as the stars move in a common circle about that center. The triangle has edge length L. What is the speed of the stars?
View Solution
Knowledge Check
The total energy of a satellite having mass m orbiting around the earth has mass M in a circular orbit with velocity v is
A12mv2B−12mv2Cmv2DGMm8Two satellite of mass m and 2 m are revolving in two circular orbits of radius r and 2r around an imaginary planet , on the surface of with gravitational force is inversely proportional to distance from its centre . The ratio of orbital speed of satellite is .
A1:1B1:2C2:1D1:√2A system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
A2Gv3πTBv3TπGCv3T2πGD2Tv3πG
Imagine a light planet revoling around a very massiv star in a circular orbit of radius R with a period of revolution T. if the gravitatinal force of attraction between the planet and the star is proportional to R−(5/2)
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo particles of masses m and 3m are moving under their mutual gravitational force, around their centre of mass, in circular orbits. The separation between the masses is r. The gravitational attraction the two provides nessary centripetal force for circular motion
The ratio of the potential energy to total kinetic energy of the system is
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View SolutionAn isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:

View Solution
