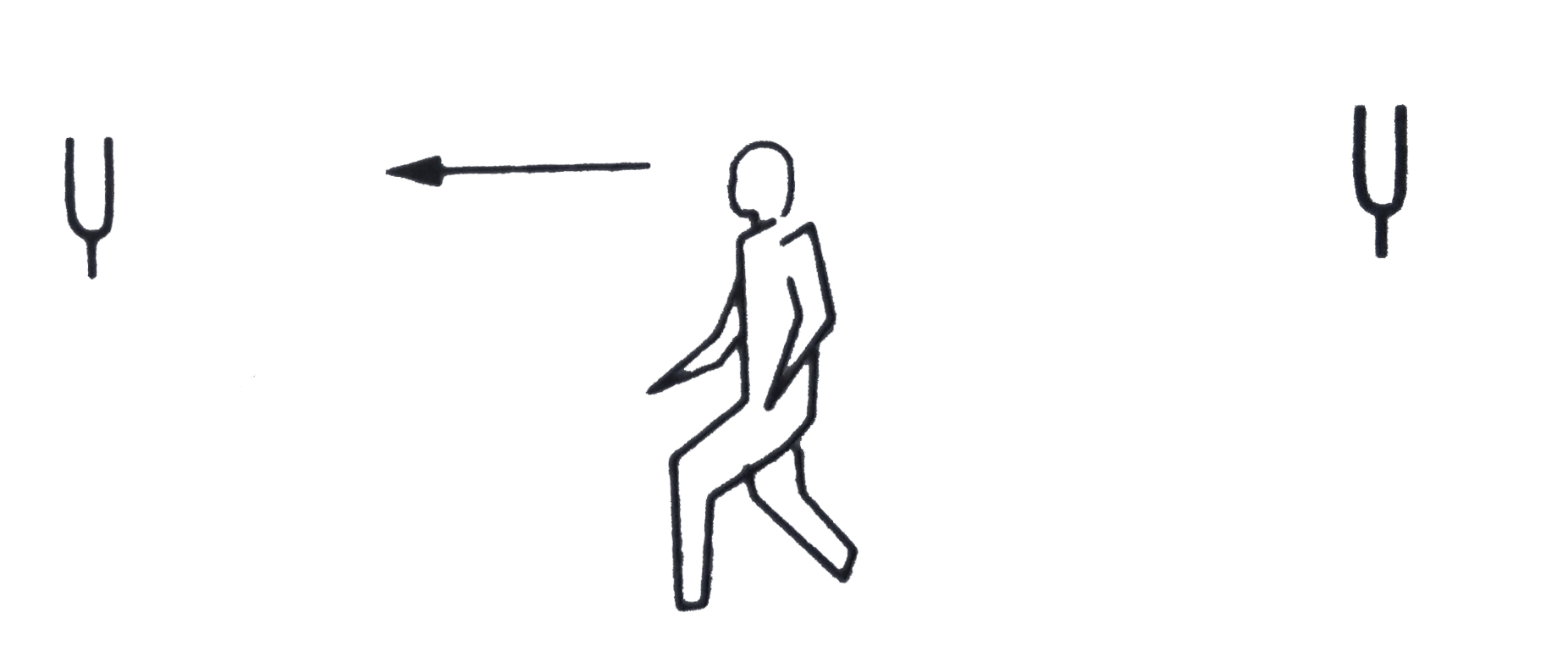
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0ms−1 so that he approaches one tuning-fork and recedes from the other. find the beat frequency bserved by the listener. Speed of sound in air =332ms−1.
.
The correct Answer is:D
Here given veolocity of he sources vs=0.<br>velocityoftheobserverv_0=3m/s<br>So,theapparentequencyheardbytheman<br>=((332+3)/332)xx256=258.3 Hz<br>Fromtheapparoχngtun∈gfork=f^1<br>Similarlyf^11=((332-3)/332)xx256<br>=253.7 Hz<br>So,beat∏ucedbythem<br>=258.3-253.7=4.6Hz
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Objective -25videos
SOUND WAVES
- BOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises32videos
SOME MECHANICAL PROPERTIES OF MATTER
- BOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises35videos
SPECIFIC HEAT CAPACITIES OF GASES
Similar Questions
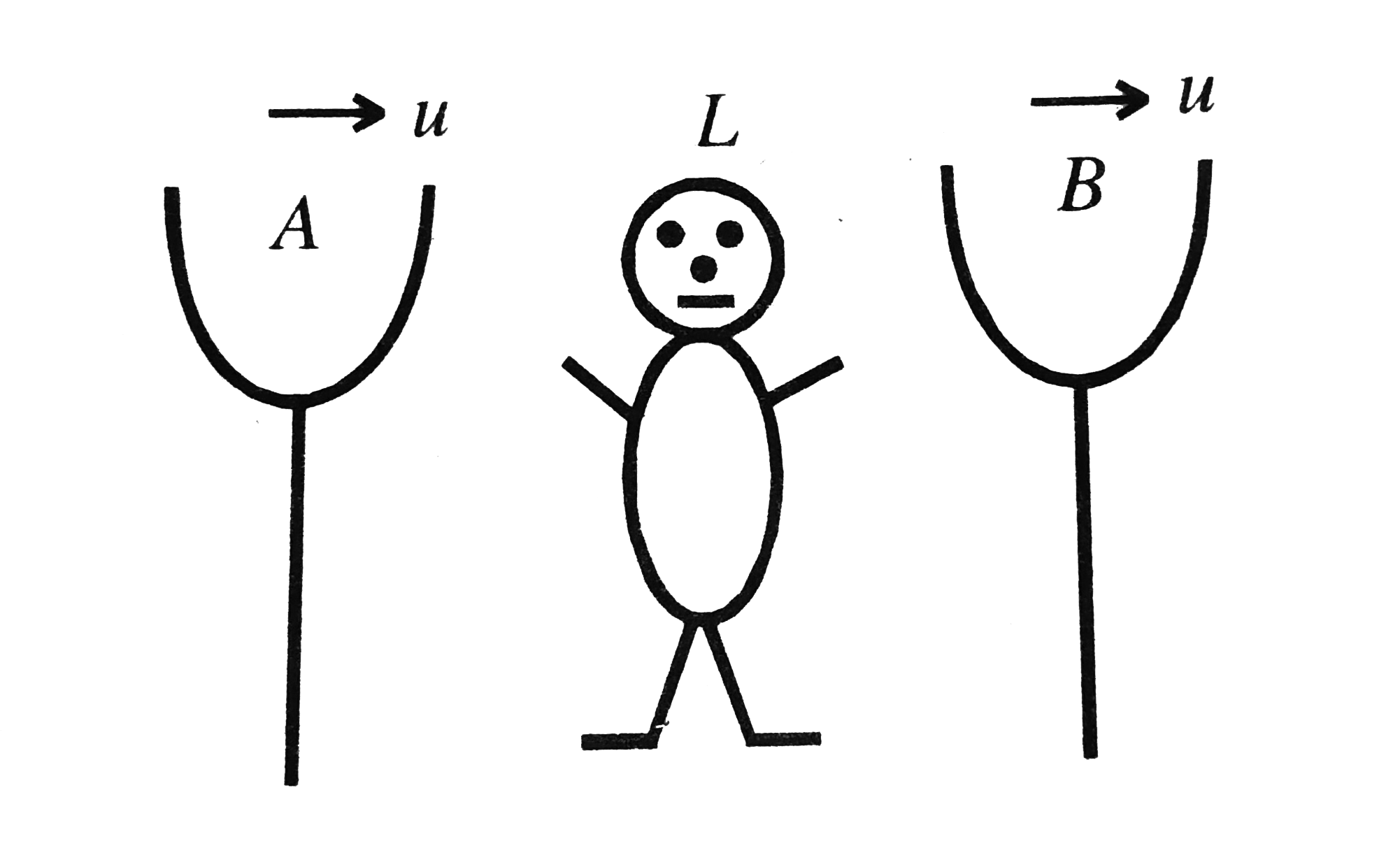Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).View SolutionFigure shows a person standing somewhere in between two identical tunning forks, each vibrating at 512Hz.If⊥hthetun∈gforksmove→wardsrightataspeedof5.5 ms^-1,f∈dtheνmberofbeatsheardbytheliste≠r.Speedofsound∈air=330 ms^-1.
View Solution
Knowledge Check
- Question 1 - Select One
With what velocity should you approach tuning fork of frequency 256 Hz so that the apparent frequency is 512 Hz. Velocity of sound in air is 340 m/s
A340 m/sB320 m/sC260 m/sD540 m/s - Question 2 - Select One
A tuning fork having frequency 256Hz emits a wave which has a wavelength of 1.35m. Find the speed of sound in air.
A256m/sB345.6m/sC245.6m/sD355.6m/s
How far does sound travel in air when a tuning fork of frequency 560Hz makes 30 vibrations ? Speed of sound in air =336m/s.
View SolutionTwo tuning forks A and B having a frequency of 500 Hz each are placed with B to the right of A. An observer in between the forks in moving towards B with a speed of 25 m/s. The speed of sound is 345 m/s and the wind speed is 5 m/s from A to B. Calculate the difference in the two frequencies heard by observer.
View SolutionTwo tuning forks are vibrating with natural frequency of 510 Hz . One tuning fork moves away from the stationary observer, while the other moves towards him at the same speed. The observer hears beats of frequency 6 Hz. The speed of each tuning fork is -- m/s. (speed of sound in air = 340m/s)
View SolutionA tuning fork is vibrating at frequency 100Hz. When another tuning fork is sounded simutaneously.=, 4 beats per second are heard. When some mass is added to the tuning fork of 100Hz, beat frequency decreases. Find the frequency of the other tuning fork.
View SolutionTwo tuning forks with natural frequencies of 340 Hz move relative to a stationary oberserver. One fork moves away from the obsorver, while the other mover towards at the same speed. The observer hears beats of freqeuency 3 Hz. Find the speed of the tuning forks assuming the velocity of sound in air to be 340 m/s.
View SolutionA tuning fork is vibrating at 250 Hz. The length of the shortest closed organ pipe that will resonate with the tuning fork will be
(Take speed of sound in air as 340ms−1)View Solution