Two identical uniform discs of mass m and radius r are arranged as shown in the figure. If α is the angular acceleration of the lower disc and acm is acceleration of centre of mass of the lower disc, then relation among acm,α and r is
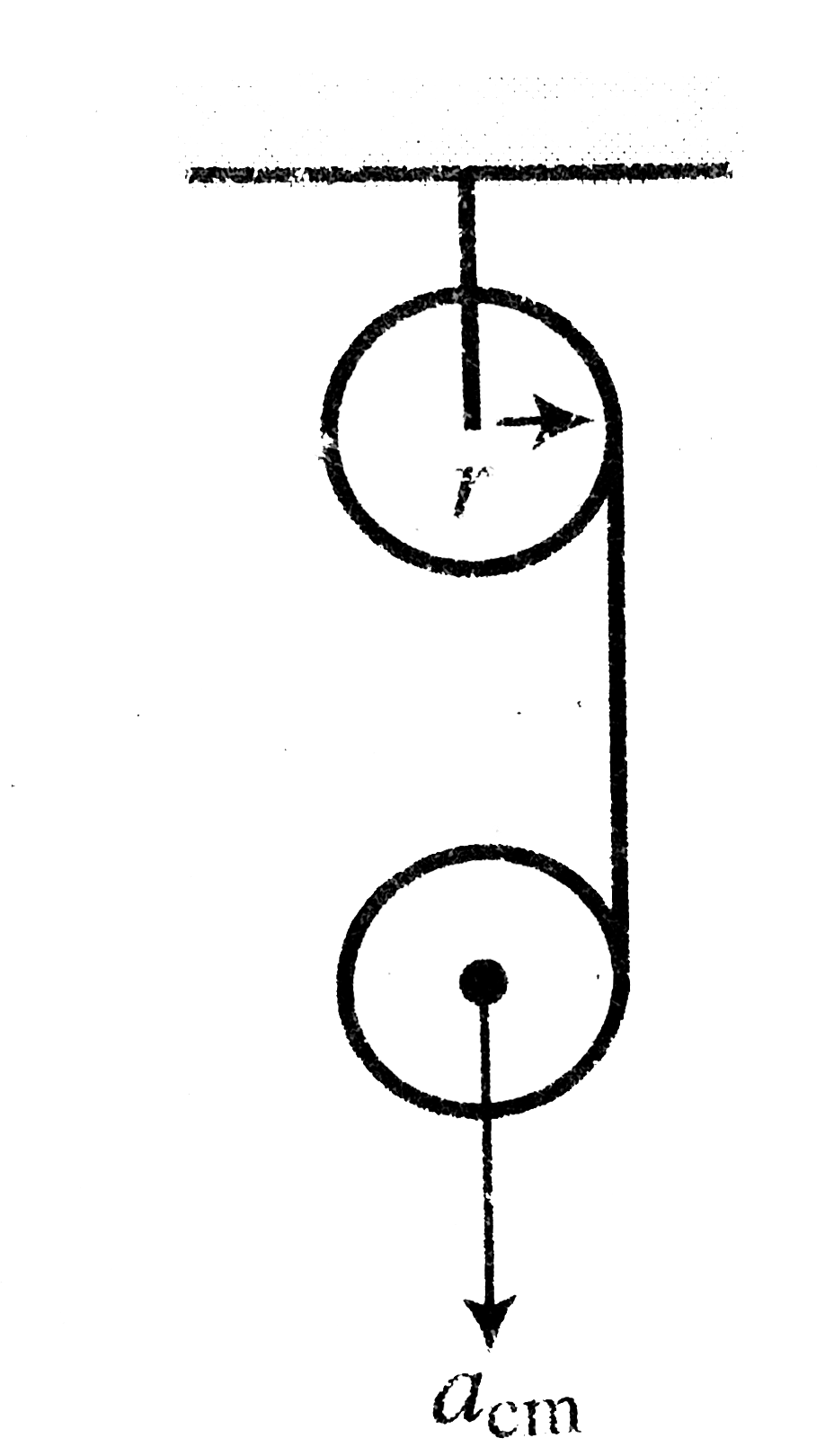
acm=αr
acm=2αr
acm=αr
none of these
The correct Answer is:B
Tr=mr22α1………….i
Tr=mr22α………….ii
α1=α…………………iii
From i and ii
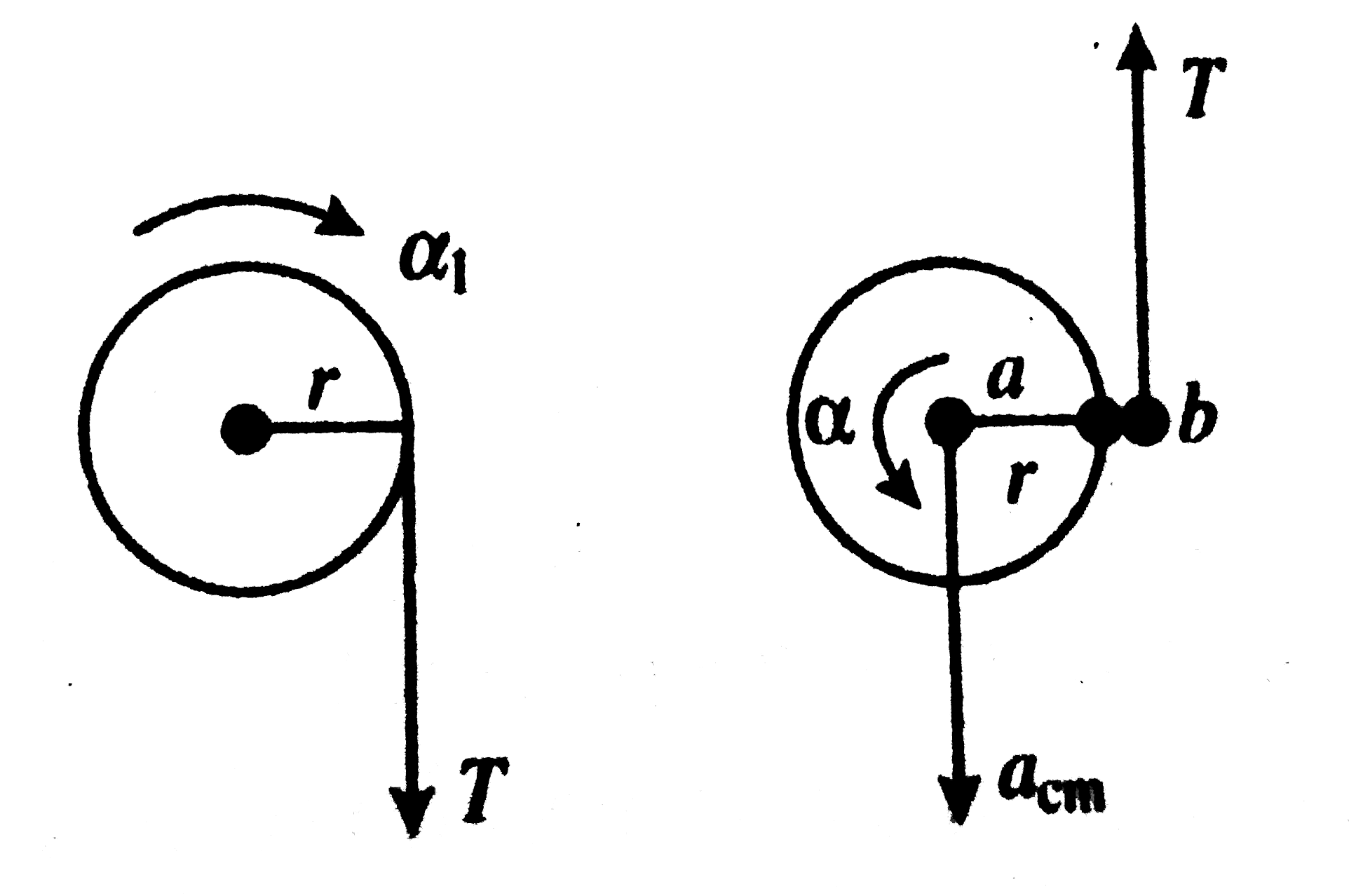
Acceleration of point b= acceleration of point a
rα1=acm−rα………..iv
Here 2raA:=acm
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
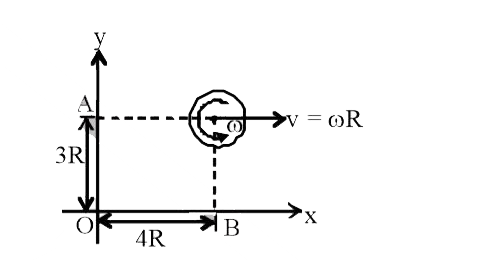
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View SolutionThree identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View Solution
Knowledge Check
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
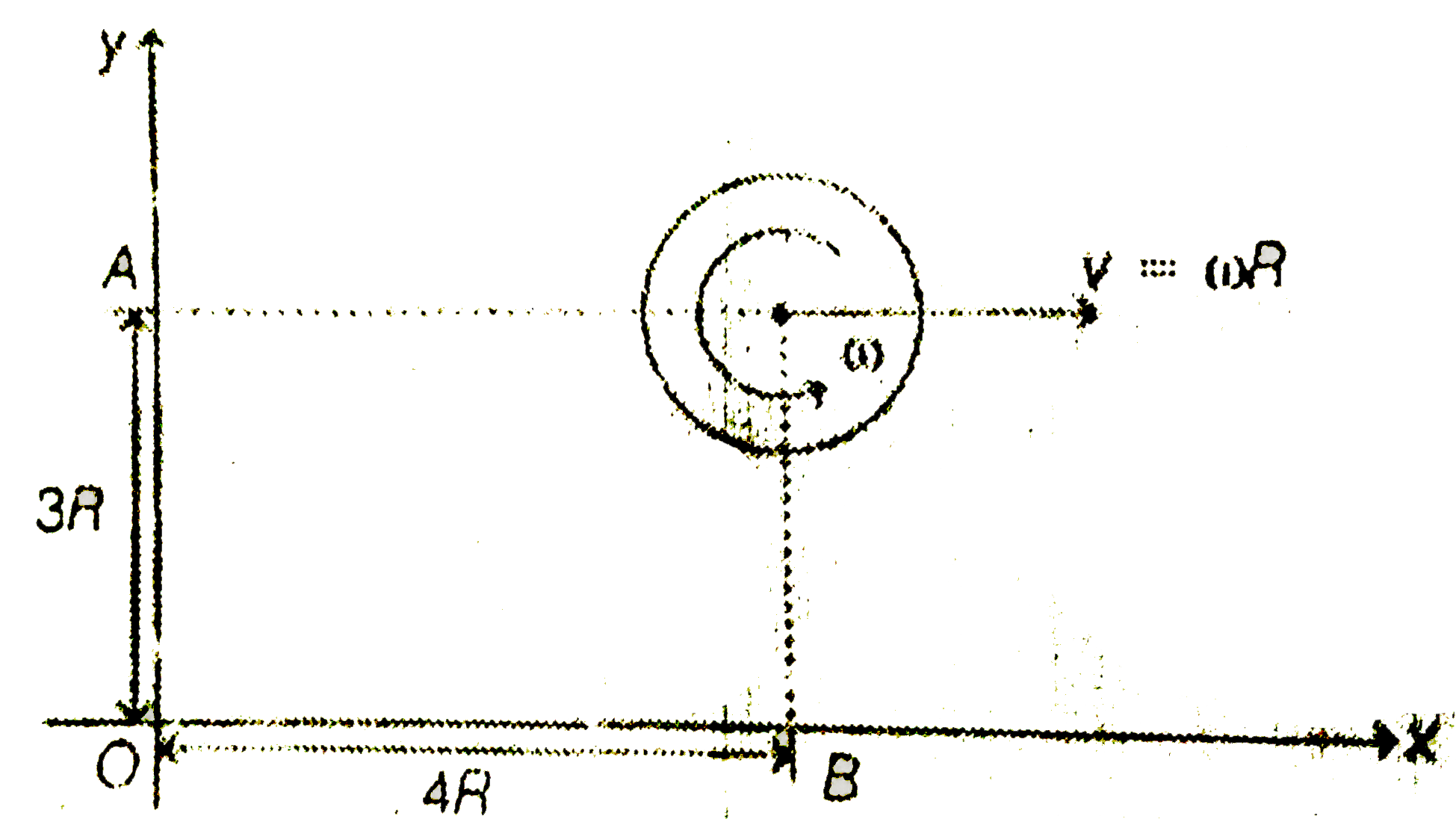 A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about A
A52mR2ω about OB72mR2ω about OC12mR2ω about AD4mR2ω about AA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
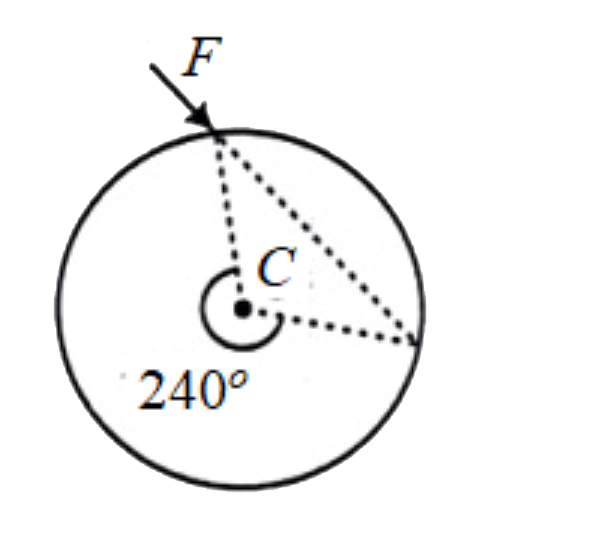 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MR
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
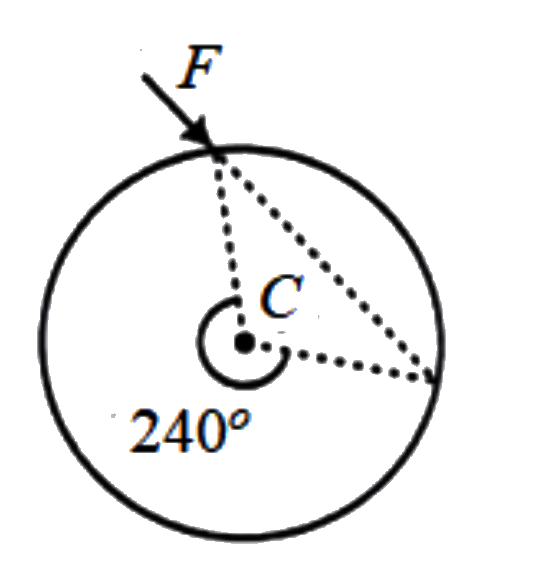
View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )

View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View Solution
