From a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

(0,0)
(0,R)
(0,√3R2)
none of these
The correct Answer is:B
Step by step video, text & image solution for From a uniform disc of radius R, an equilateral triangle of side sqrt(3)R is cut as shown in the figure. The new position of centre of mass is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-2
21 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - L-3,(P-1)
5 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example
50 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
Similar Questions
The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionA thin disc of mass 9M and radius R is given.Now a disc of radius (R/3) is cut as shown in figure.The new position of C .m from orgin will be :-
View Solution
Knowledge Check
From a uniform disc of radius R, an equilibatered triangle of side √3R is cut as shown. The new position of centre of mass is:
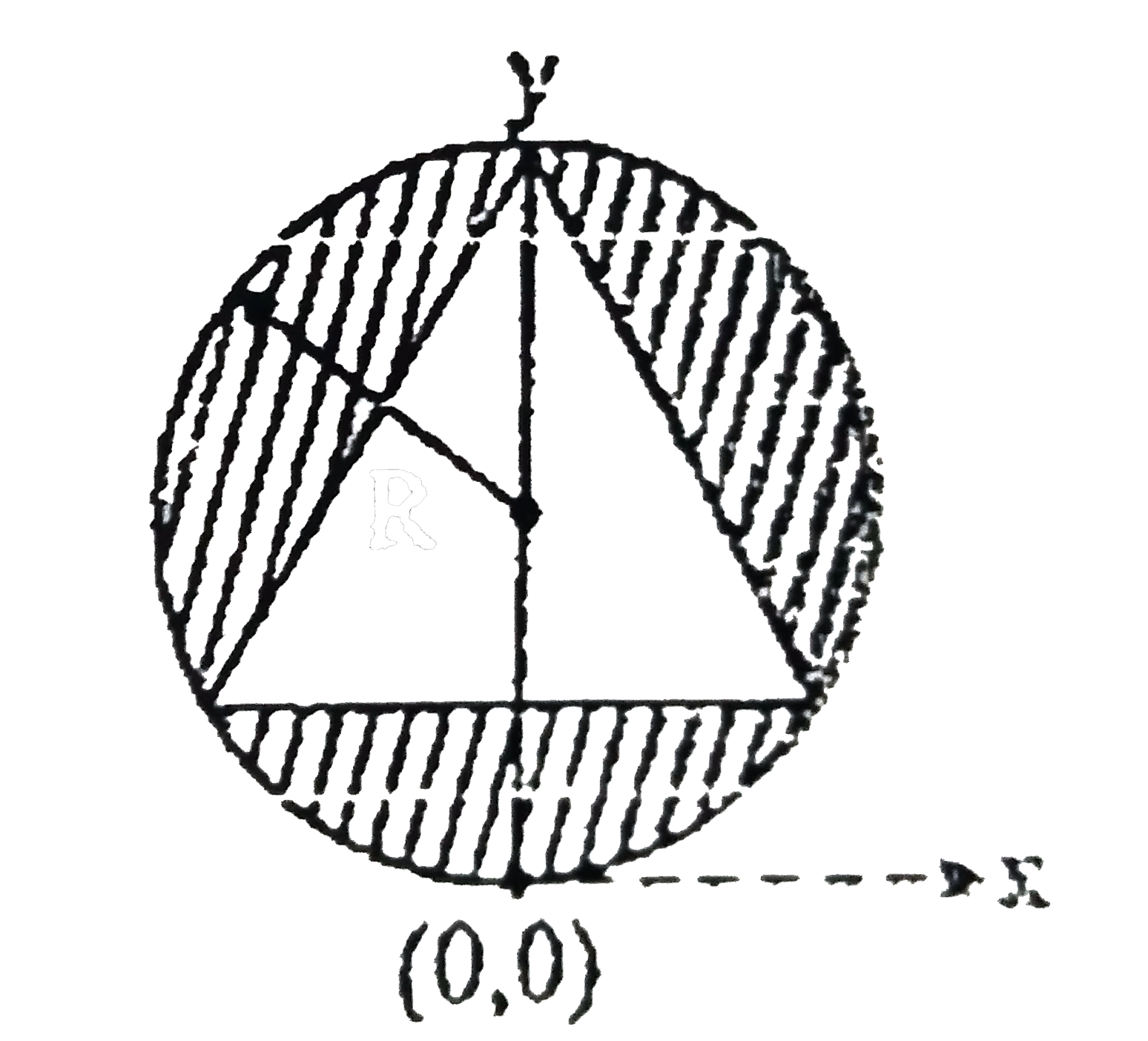 A(0,0)B(0,R)C(0,√3R2)Dnone of these
A(0,0)B(0,R)C(0,√3R2)Dnone of theseA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),
 Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .
Aits linear acceleration is g upwardBits linear acceleration is g downwardCits angular acceleration is 2gR .Dits rate of change of angular momentum is MgR .From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
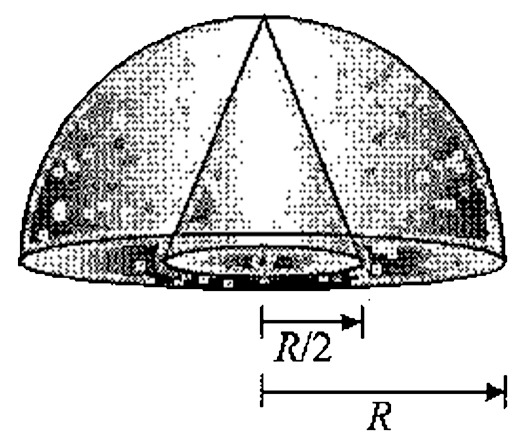
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution